12.6.Perceptron

Linux 5.4.0-80-generic
Python 3.9.5 @ GCC 7.3.0
Latest build date 2021.07.31

import os
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from sklearn.metrics import accuracy_score
from toolkit.blog.util import get_md_dir

生成样本

生成一个线性可分的样本集

X, y_0_1 = make_classification(n_samples=100, n_features=2, n_classes=2,
                               n_informative=2, n_redundant=0,
                               n_repeated=0,
                               n_clusters_per_class=1, flip_y=0,
                               random_state=3)

对target赋予其他值：

# 反转数据
y_1_0 = np.array([1 if i == 0 else 0 for i in y_0_1])
# -1-1数据
y_1_1 = np.array([-1 if i == 0 else 1 for i in y_0_1])
# -3-10数据
y_1_10 = np.array([-3 if i == 1 else 10 for i in y_0_1])

绘制训练数据的图像，可以发现数据是线性可分的，根据感知机的理论，感知机算法必定能找到一条直线，将两类样本完全分开。

定义画图函数

def plot_perceptron(w_1, w_2, b, X, y, filename=None, title=None):  # noqa
    x2 = np.arange(X[:, 1].min(), X[:, 1].max(), 0.01)  # noqa
    x1 = -(w_2 * x2 + b) / w_1

    labels = np.sort(np.unique(y))
    X_zero, X_one = X[y == labels[0]], X[y == labels[1]]  # noqa
    label_zero, label_one = str(labels[0]), str(labels[1])

    plt.figure(figsize=(5, 4))
    plt.scatter(X_one[:, 0], X_one[:, 1], color='steelblue', label=label_one)
    plt.scatter(X_zero[:, 0], X_zero[:, 1], color='darkorange',
                label=label_zero)
    plt.plot(x1, x2, color='darkolivegreen', label='perceptron', lw=3)
    plt.legend(fontsize=11)
    if title is not None:
        plt.title(f"{title}\nw1={round(w_1, 4)} w2={round(w_2, 4)} "
                  f"b={round(b, 4)}", fontsize=13)
    if filename is not None:
        plt.savefig(os.path.join(get_md_dir(), "figures", filename))
    plt.show()

手动实现感知机

Perceptron 算法于 1958 年由 Frank Rosenblatt 在康奈尔航空实验室发明，这个项目由美国海军研究办公室资助。最开始的 Perceptron 旨在成为一台专门用于图像识别的机器，而不是一个程序，虽然它的第一个实现是在 IBM 704 的软件中实现的。当时，美国海军组织对 Perceptron 寄予厚望，希望它能够走路、说话、看、写、复制自己并意识到它的存在。尽管感知器最初看起来很有前途，但很快就证明感知器无法通过训练来识别多类别的模式，这导致神经网络研究领域停滞多年。1969年，由 Marvin Minsky 和 Seymour Papert 撰写的书籍 Perceptrons 表明：感知机算法无法解决异或问题，并推测多层感知机网络也无法解决异或问题。

Perceptron 类是手动实现的 Rosenblatt 感知机，以随机梯度下降的方式更新权重，且支持两种损失函数：

1. 误分类点到 Perceptron 直线的距离
2. 平方损失

from toolkit.example.perceptron import Perceptron

model = Perceptron(iteration=100, learn_rate=0.02, loss="distance",
                   use_bias=True, kernel_initializer=0., bias_initializer=0.)

model.fit(X, y_0_1, verbose=False)

print("weights:", model.weights)

print("bias:   ", model.bias)
y_predict = model.predict(X)
print("accuracy score:", accuracy_score(y_0_1, y_predict))

(w_1, w_2), b = model.weights, model.bias
plot_perceptron(w_1, w_2, b, X, y_0_1, "my_perceptron.svg", "My Perceptron")

weights: [-0.13499787 -0.0660545 ]
bias:    0.02
accuracy score: 1.0

测试 1-0 标签

对 Perceptron 测试 1-0 target。

model_1 = Perceptron(iteration=100, learn_rate=0.02, loss="square",
                     use_bias=True, kernel_initializer=0., bias_initializer=0.)
model_1.fit(X, y_1_0)
# 输出权重、偏置信息
print("weights:", model_1.weights)
print("bias:   ", model_1.bias)
# 进行预测
y_predict = model_1.predict(X)
print("accuracy score:", accuracy_score(y_1_0, y_predict))

weights: [0.12463955 0.05923452]
bias:    -0.02
accuracy score: 1.0

测试 -1-1 标签

model_2 = Perceptron(iteration=100, learn_rate=0.02, loss="square",
                     use_bias=True, kernel_initializer=0., bias_initializer=0.)
model_2.fit(X, y_1_1)
# 输出权重、偏置信息
print("weights:", model_2.weights)
print("bias:   ", model_2.bias)

y_predict = model_2.predict(X)
print("accuracy score:", accuracy_score(y_1_1, y_predict))

weights: [-0.13499787 -0.0660545 ]
bias:    0.02
accuracy score: 1.0

梯度下降可视化

下图为手动实现的 Perceptron 算法在训练时，随机梯度下降的过程。因为三维空间中只能绘制两个变量，所以偏置（截距）固定为 0。随机梯度下降只更新两个权重的值，且权重$w_1$和$w_2$分别初始化为 0.3 和 0.2，学习率为常数 0.002，使用平方损失。

可以发现，在损失函数较平滑的地方，梯度下降较为缓慢，在损失函数较陡峭的地方，梯度下降较快。在靠近最小值点时，由于学习率固定不变，好几次越过了最小值点而反复横跳。学习率设置得越大，震荡就会越明显。

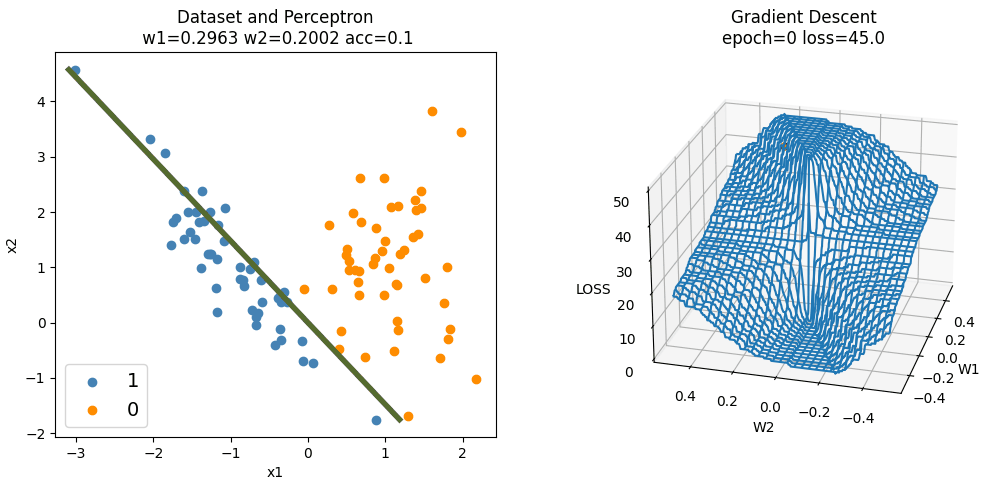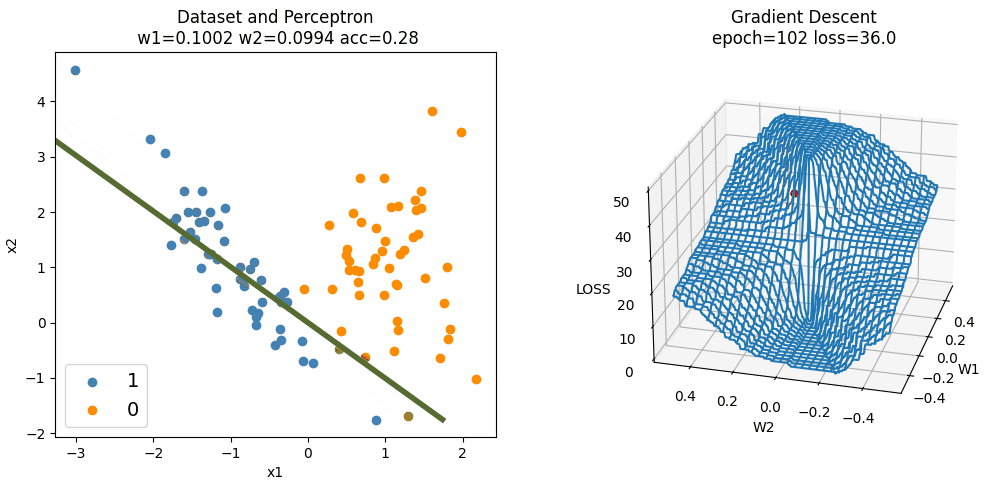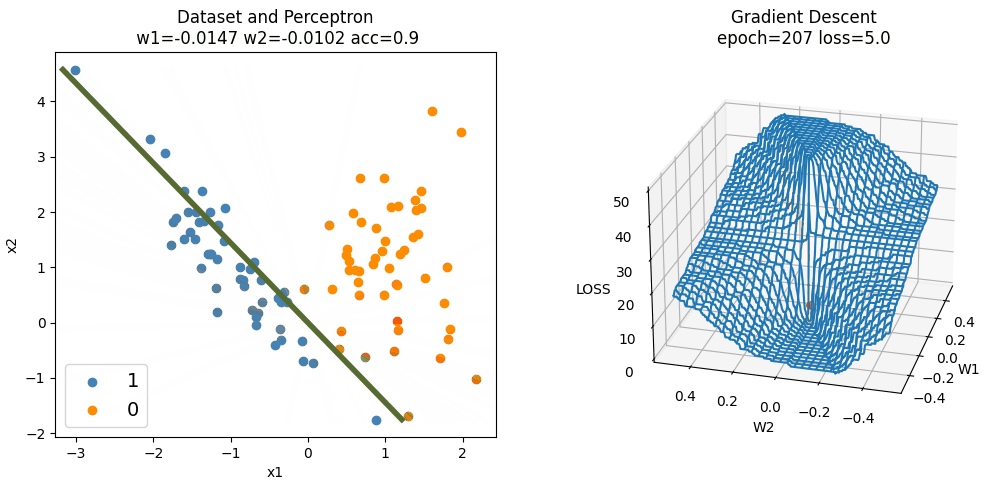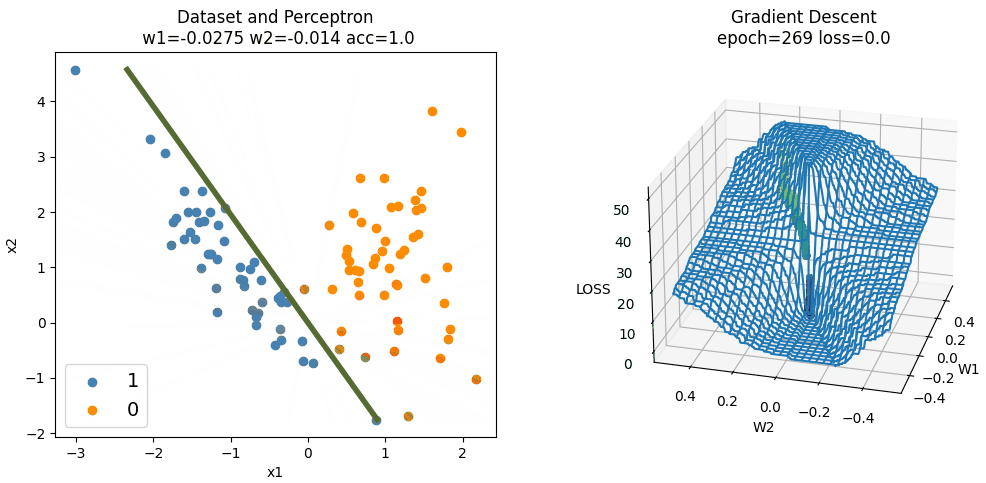
容易看出，权重初始值和学习率直接影响训练所需的迭代次数(epoch)，权重初始值离(局部)最小值点越远，学习率越小，需要的迭代次数越多。

scikit-learn 感知机

sklearn.linear_model.Perceptron

Perceptron(penalty=None, alpha=0.0001, l1_ratio=0.15, fit_intercept=True,
           max_iter=1000, tol=0.001, shuffle=True, verbose=0, eta0=1.0,
           n_jobs=None, random_state=0, early_stopping=False,
           validation_fraction=0.1, n_iter_no_change=5, class_weight=None,
           warm_start=False)

• penalty: {‘l2’,’l1’,’elasticnet’}，要使用的正则化项（惩罚项）。

• alpha: float，正则化项的系数，是一个常数。

• l1_ratio: float，0 <= l1_ratio <= 1，弹性网络混合参数，仅当penalty='elasticnet'时生效。 l1_ratio=0时即是 L2 正则项，l1_ratio=1时即是 L1 正则项。New in version 0.24.

• fit_intercept: 是否拟合截距（偏置）。fit_intercept=False即是假设数据已经中心化。

• max_iter: 整个训练集的最大迭代次数，该参数又名为epochs。 仅影响fit方法，不会影响partial_fit方法。New in version 0.19.

• tol: float，早停规则。如果设置了tol，则训练会在 (loss > previous_loss - tol) 时停止。New in version 0.19.

• shuffle: 是否在每个epoch完成之后打乱训练集。

• eta0: 梯度下降的学习率。

• n_jobs: 执行 OVA (One Versus All, for multi-class problems) 计算时，使用的 CPU 核心数。

• random_state: 随机数种子。当 shuffle=True 时，设置该参数可以重现训练过程。

• early_stopping: 是否早停。如果early_stopping=True，将自动留出一部分数据用于验证模型， 并在连续 n_iter_no_change 次迭代 (epochs) 后，验证分数都没有提高至少 tol 时，停止训练。New in version 0.20.

• validation_fraction: float，用于早停的验证集大小，介于0与1之间。仅当early_stopping=True时生效。New in version 0.20.

• n_iter_no_change: int，若n_iter_no_change次迭代后，验证集上的损失没有显著下降，则停止训练。New in version 0.20.

• warm_start: 是否使用上一次训练得到的权重与偏置进行初始化， 参考 the Glossary。

trainingverbose

from sklearn.linear_model import Perceptron

perceptron = Perceptron(penalty='l1', alpha=0.0001, fit_intercept=True,
                        max_iter=100, tol=1e-3, shuffle=True, verbose=1,
                        eta0=1, n_jobs=-1, random_state=1, early_stopping=False,
                        validation_fraction=0.1, n_iter_no_change=5,
                        class_weight=None, warm_start=False)

perceptron.fit(X, y_0_1)

-- Epoch 1
Norm: 3.79, NNZs: 2, Bias: 1.000000, T: 100, Avg. loss: 0.045638
Total training time: 0.00 seconds.
-- Epoch 2
Norm: 4.88, NNZs: 2, Bias: 2.000000, T: 200, Avg. loss: 0.049804
Total training time: 0.00 seconds.
-- Epoch 3
Norm: 4.39, NNZs: 2, Bias: 2.000000, T: 300, Avg. loss: 0.053986
Total training time: 0.00 seconds.
-- Epoch 4
Norm: 4.76, NNZs: 2, Bias: 0.000000, T: 400, Avg. loss: 0.016852
Total training time: 0.00 seconds.
-- Epoch 5
Norm: 5.20, NNZs: 2, Bias: 1.000000, T: 500, Avg. loss: 0.031670
Total training time: 0.00 seconds.
-- Epoch 6
Norm: 6.04, NNZs: 2, Bias: 1.000000, T: 600, Avg. loss: 0.026127
Total training time: 0.00 seconds.
-- Epoch 7
Norm: 6.53, NNZs: 2, Bias: 1.000000, T: 700, Avg. loss: 0.039767
Total training time: 0.00 seconds.
-- Epoch 8
Norm: 6.58, NNZs: 2, Bias: 1.000000, T: 800, Avg. loss: 0.027038
Total training time: 0.00 seconds.
-- Epoch 9
Norm: 6.58, NNZs: 2, Bias: 1.000000, T: 900, Avg. loss: 0.000000
Total training time: 0.00 seconds.
-- Epoch 10
Norm: 6.58, NNZs: 2, Bias: 1.000000, T: 1000, Avg. loss: 0.000000
Total training time: 0.00 seconds.
-- Epoch 11
Norm: 6.58, NNZs: 2, Bias: 1.000000, T: 1100, Avg. loss: 0.000000
Total training time: 0.00 seconds.
-- Epoch 12
Norm: 6.58, NNZs: 2, Bias: 1.000000, T: 1200, Avg. loss: 0.000000
Total training time: 0.00 seconds.
-- Epoch 13
Norm: 6.58, NNZs: 2, Bias: 1.000000, T: 1300, Avg. loss: 0.000000
Total training time: 0.00 seconds.
-- Epoch 14
Norm: 6.58, NNZs: 2, Bias: 1.000000, T: 1400, Avg. loss: 0.000000
Total training time: 0.00 seconds.
Convergence after 14 epochs took 0.00 seconds

Perceptron(eta0=1, max_iter=100, n_jobs=-1, penalty='l1', random_state=1,
           verbose=1)

W, b = perceptron.coef_, perceptron.intercept_[0]  # noqa
print("weights:", W)
print("bias:   ", b)
y_predict = perceptron.predict(X)
print("accuracy score:", accuracy_score(y_0_1, y_predict))

plot_perceptron(W[0, 0], W[0, 1], b, X, y_0_1,
                "sk_perceptron_0_1.svg", "scikit-learn Perceptron")

weights: [[-5.81308582 -2.71686054]]
bias:    1.0
accuracy score: 1.0

可以验证，scikit learn 感知机输出的预测结果是符合以下公式的：

y_decision_predict = perceptron.decision_function(X)
y_decision_predict_mu = np.matmul(X, perceptron.coef_.reshape(2, 1)) + b
all(y_decision_predict == y_decision_predict_mu.flatten())  # noqa

True

scikit learn 感知机可以自适应不同的数据标签，即 scikit-learn 的优化方法不固定于 y 的label。

对 scikit-learn Perceptron 测试 1-0 target：

perceptron.verbose = 0
perceptron.fit(X, y_1_0)
y_predict = perceptron.predict(X)
W, b = perceptron.coef_, perceptron.intercept_[0]  # noqa
print("weights:", W)
print("bias:   ", b)
print("accuracy score:", accuracy_score(y_1_0, y_predict))

weights: [[5.81308582 2.71686054]]
bias:    -1.0
accuracy score: 1.0

对 scikit-learn Perceptron 测试 -1-1 target。

perceptron.fit(X, y_1_1)
y_predict = perceptron.predict(X)
W, b = perceptron.coef_, perceptron.intercept_[0]  # noqa
print("weights:", W)
print("bias:   ", b)
print("accuracy score:", accuracy_score(y_1_1, y_predict))

weights: [[-5.81308582 -2.71686054]]
bias:    1.0
accuracy score: 1.0

对 scikit-learn Perceptron 测试 -3-10 target。

perceptron.fit(X, y_1_10)
y_predict = perceptron.predict(X)
W, b = perceptron.coef_, perceptron.intercept_[0]  # noqa
print("weights:", W)
print("bias:   ", b)
print("accuracy score:", accuracy_score(y_1_10, y_predict))

weights: [[5.81308582 2.71686054]]
bias:    -1.0
accuracy score: 1.0

TensorFlow 感知机

奇怪的感知机

import tensorflow as tf
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense

model = Sequential()
model.add(Dense(1, activation="softsign", input_shape=(2,),
                use_bias=True))

model.compile(optimizer="SGD", loss='mean_squared_error', metrics=['accuracy'])
result = model.fit(X, y_0_1.reshape(-1, 1), batch_size=16, epochs=500)

y_predict = (model.predict(X) > 0.5).astype('int32')

W, b = model.get_weights()
print("weights:", W)
print("bias:   ", b)
print("accuracy score:", accuracy_score(y_0_1, y_predict))

plot_perceptron(float(W[0, 0]), float(W[1, 0]), float(b[0]), X, y_0_1,
                "keras_perceptron_softsign_0_1.svg", "keras Perceptron")

weights: [[-1.0029898 ]
 [-0.07301947]]
bias:    [1.2841063]
accuracy score: 0.98

我们基于 Keras 实现了感知机模型，但 Keras 的感知机显然有点奇怪。按照 Rosenblatt 的感知机理论，感知机直线应该将两类样本点划分开来，但上图的感知机直线却使得两类样本点混杂在一起，然而模型预测结果的准确率却高达 0.98。

究竟是哪里出了问题呢？细心的读者可能已经发现，以上模型使用的激活函数是 softsign 函数，并不是 Rosenblatt 感知机所用的越阶函数。既然使用的激活函数不同，为什么最终还可以达到这么高的准确率呢？其实，这是由梯度下降算法保障的，梯度下降算法会尽量让感知机在训练集上的输出值逼近真实值。

既然如此，那是不是将 softsign 激活函数改为越阶激活函数就可以实现 Rosenblatt 感知机了呢？但 TensorFlow 或 Keras 并没有提供越阶激活函数，因为 TensorFlow 利用自动微分寻找最优的权重值，但越阶函数的梯度处处为0，这会导致梯度消失，模型无法训练。

Keras 如何实现感知机

虽然我们无法在 TensorFlow 模型中使用越阶函数，但可以用 hard_sigmoid 函数去近似代替越阶函数，这样可以近似地实现一个 Rosenblatt 感知机。

model = Sequential()
model.add(Dense(1, activation="hard_sigmoid", input_shape=(2,),
                use_bias=True))

model.compile(optimizer="SGD", loss='mean_squared_error', metrics=['accuracy'])
result = model.fit(X, y_0_1.reshape(-1, 1), batch_size=16, epochs=200)

# model.predict_classes(X)
y_predict = (model.predict(X) > 0.5).astype('int32')
W, b = model.get_weights()
print("weights:", W)
print("bias:   ", b)
print("accuracy score:", accuracy_score(y_0_1, y_predict))

plot_perceptron(float(W[0, 0]), float(W[1, 0]), float(b[0]), X, y_0_1,
                "keras_perceptron_16_batch_0_1.svg", "keras Perceptron")

weights: [[-1.3330553 ]
 [-0.05380743]]
bias:    [-0.02743404]
accuracy score: 0.98

现在上图的感知机模型效果图看起来正常多了，但还有一个问题：数据集是线性可分的，但上述模型要达到百分百的准确率似乎并不容易。

要弄清楚这个问题，需要先熟悉 Rosenblatt 感知机理论。Rosenblatt 感知机算法每次只使用一个分类错误的样本点更新权重，也就是随机梯度下降的方式。而上述模型则是使用批梯度下降的方式更新权重，每批次为16个样本。显然，16个样本的平均梯度和1个样本的梯度是有一点差异的。那么，我们来测试一下 batch_size=1 的效果：

model = Sequential()
model.add(Dense(1, activation="hard_sigmoid", input_shape=(2,),
                use_bias=True, kernel_initializer='zeros',
                bias_initializer='zeros'))

model.compile(optimizer="SGD", loss='mean_squared_error', metrics=['accuracy'])
result = model.fit(X, y_0_1.reshape(-1, 1), batch_size=1, epochs=200)

y_predict = (model.predict(X) > 0.5).astype('int32')
W, b = model.get_weights()
print("weights:", W)
print("bias:   ", b)
print("accuracy score:", accuracy_score(y_0_1, y_predict))

plot_perceptron(float(W[0, 0]), float(W[1, 0]), float(b[0]), X, y_0_1,
                "keras_perceptron_incorrect_sgd_0_1.svg", "keras Perceptron")

weights: [[-3.5219226]
 [-1.1625581]]
bias:    [0.75313836]
accuracy score: 0.98

结果出乎意料，即使将batch_size设置为1，Keras Perceptron 的准确率还是无法达到1。实际上，这与学习率也有关系，有时，我们需要选取一个恰当的梯度下降策略，才能找到最优的权重值。

model = Sequential()
model.add(Dense(1, activation="hard_sigmoid", input_shape=(2,),
                use_bias=True, kernel_initializer='zeros',
                bias_initializer='zeros'))

sgd = tf.optimizers.SGD(lr=0.01, decay=1e-6, momentum=0.9, nesterov=True)
model.compile(optimizer=sgd, loss='mean_squared_error', metrics=['accuracy'])
result = model.fit(X, y_0_1.reshape(-1, 1), batch_size=1, epochs=200)

y_predict = (model.predict(X) > 0.5).astype('int32')
W, b = model.get_weights()
print("weights:", W)
print("bias:   ", b)
print("accuracy score:", accuracy_score(y_0_1, y_predict))

plot_perceptron(float(W[0, 0]), float(W[1, 0]), float(b[0]), X, y_0_1,
                "keras_perceptron_0_1.svg", "keras Perceptron")

weights: [[-6.69984 ]
 [-3.005875]]
bias:    [0.98682415]
accuracy score: 1.0