概率论与数理统计
siwing
2020 年 8 月 27 日
2
目录
第一部分 概率论初步 1
1 概率的本质 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
1.1 贝叶斯派(主观概率派) . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
1.2 频率学派 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
1.3 总结 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
1.4 如何理解概率 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
2 测度 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
2.1 幂集 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
2.2 σ 代数 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
2.3 测度 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
2.4 概率测度 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
2.4.1 条件概率 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
2.4.2 Borel 域 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
2.4.3 勒贝格不可测集 . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
2.4.4 开集与闭集的概率 . . . . . . . . . . . . . . . . . . . . . . . . . . 7
3 概率的公式 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
3.1 加法公式 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
3.2 乘法公式 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8
3.2.1 条件概率 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8
3.2.2 乘法公式 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8
3.3 全概率公式 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
3.4 贝叶斯公式 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
3.5 总结 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
4 独立与不相关 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11
4.1 事件的独立性 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11
4.2 试验的独立性 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
4.3 随机变量的独立性 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
4.4 线性相关性 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
4.5 不相关与独立的关系 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
3
目录
第二部分 基础概率论 15
5 随机变量 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17
5.1 离散型随机变量 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17
5.2 连续型随机变量 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17
6
概率分布
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17
6.1 分布函数(概率分布函数) . . . . . . . . . . . . . . . . . . . . . . . . . . 17
6.2 分布列 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
6.3 概率密度函数 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
6.4 总结 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
7 期望 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
7.1 期望的性质 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
8 方差 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
8.1 方差的性质 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20
8.2 切比雪夫不等式 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20
9 排列组合 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
10 一维离散分布 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23
10.1 二项分布 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23
10.1.1
期望与方差的推导
. . . . . . . . . . . . . . . . . . . . . . . . . . 23
10.1.2 二项分布期望与方差的简单推导 . . . . . . . . . . . . . . . . . . 24
10.1.3 名字由来 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25
10.2 伯努利分布(0 − 1 分布) . . . . . . . . . . . . . . . . . . . . . . . . . . . 25
10.3 泊松分布 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25
10.3.1 推导泊松分布 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25
10.3.2 泊松分布期望和方差的推导 . . . . . . . . . . . . . . . . . . . . . 26
10.3.3 poisson 分布的由来 . . . . . . . . . . . . . . . . . . . . . . . . . 27
10.4 超几何分布 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27
10.4.1 超几何分布的期望和方差 . . . . . . . . . . . . . . . . . . . . . . 28
10.5 负二项分布(帕斯卡分布) . . . . . . . . . . . . . . . . . . . . . . . . . . 28
10.5.1 名字由来 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29
10.6 几何分布 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29
10.6.1 几何分布的期望和方差 . . . . . . . . . . . . . . . . . . . . . . . 29
10.6.2 几何分布的无记忆性 . . . . . . . . . . . . . . . . . . . . . . . . . 30
10.6.3 名字由来 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30
11 各一维离散分布的联系 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30
11.1 总结 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31
12 一维连续分布 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31
12.1 正态分布(Gauss 分布) . . . . . . . . . . . . . . . . . . . . . . . . . . . 31
12.1.1 标准正态分布 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31
4
目录
12.1.2 正态分布的期望和方差 . . . . . . . . . . . . . . . . . . . . . . . 31
12.2 均匀分布 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32
12.2.1 名字的由来 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32
12.3 指数分布与其无记忆性 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32
12.3.1 负指数一词的由来 . . . . . . . . . . . . . . . . . . . . . . . . . . 32
12.4 Weibull 分布 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32
12.5 伽马分布 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33
12.5.1 伽马分布的性质 . . . . . . . . . . . . . . . . . . . . . . . . . . . 33
12.5.2 伽马分布的两个特例 . . . . . . . . . . . . . . . . . . . . . . . . . 33
12.6 贝塔分布 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33
13 随机变量函数的分布 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 34
13.1 分布函数法 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 34
13.1.1 步骤 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 34
13.2 定理法 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 34
14 分布的其它特征数 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 36
14.1 k 阶矩 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 36
14.1.1 中心矩与原点矩的关系 . . . . . . . . . . . . . . . . . . . . . . . 37
14.2 变异系数(离散系数) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 37
14.3 分位数 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 37
14.4 中位数 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 38
14.5 偏度 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 38
14.6 峰度 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 38
15 参考文献 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 38
第三部分 概率论进阶 39
16 随机变量序列的四种收敛 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 41
17 大数定律 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 42
17.1 伯努利大数定律 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 42
17.2 大数定律一般形式 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 43
17.3 切比雪夫大数定律 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 43
17.4 马尔可夫大数定律 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 44
17.5 辛钦大数定律 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 44
17.6 总结 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 44
18 中心极限定理 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 45
18.1 独立同分布下的中心极限定理 . . . . . . . . . . . . . . . . . . . . . . . . . 45
18.2 二项分布的正态近似 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 45
18.3 独立不同分布下的中心极限定理 . . . . . . . . . . . . . . . . . . . . . . . . 45
5
目录
第四部分 数理统计 47
19 抽样分布 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 49
19.1 统计学分布 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 49
19.2 抽样分布的作用 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 50
19.3
三大抽样分布
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 51
19.3.1 χ
2
分布 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 51
19.3.2 t 分布 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 52
19.3.3 F 分布 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 53
19.4 样本均值 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 54
19.5 样本方差与样本标准差 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 55
19.6 一些重要的结论 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 56
20 参数估计 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 57
20.1 矩估计 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 57
20.1.1 缺陷 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 58
20.2 极 (最) 大似然估计 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 58
20.3 点估计 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 59
20.4 区间估计 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 59
20.4.1
构造置信区间——枢轴量法
. . . . . . . . . . . . . . . . . . . . . 60
20.4.2 构造置信区间的原则 . . . . . . . . . . . . . . . . . . . . . . . . . 60
20.4.3 区间估计与点估计的联系 . . . . . . . . . . . . . . . . . . . . . . 61
20.5 点估计量的评判标准 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 61
20.5.1 相合性 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 61
20.5.2 无偏性 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 62
20.5.3 有效性 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 62
20.5.4 直观理解各标准的区别 . . . . . . . . . . . . . . . . . . . . . . . 62
20.6 判断 UMVUE . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 63
21 假设检验 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 64
21.1 小概率原理与统计归谬法 . . . . . . . . . . . . . . . . . . . . . . . . . . . 64
21.2 相关概念 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 65
21.3 α 错误 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 66
21.4 P 值 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 68
21.4.1 P 值危机 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 68
22 抽样分布、参数估计、假设检验的联系 . . . . . . . . . . . . . . . . . . . . . . . . 71
23 概念基础 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 72
23.1 统计量的极限分布、大样本与小样本 . . . . . . . . . . . . . . . . . . . . . 72
23.2 充分统计量 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 72
23.3 参数估计 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 72
23.3.1 点估计 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 73
6
23.3.2 极大似然估计 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 73
23.3.3 矩估计与极大似然估计 . . . . . . . . . . . . . . . . . . . . . . . 73
23.3.4 区间估计 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 73
参考文献 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 75
第一部分
概率论初步
1

1 概率的本质
1 概率的本质
如何定义概率是一个很难的问题,甚至我们难以确定这个世界是否存在概率。换而言之,这个世
界真的存在随机吗?而概率又是统计学的核心,因此有必要探讨一下概率的本质。
出于对世界是否随机问题的不同认知,统计学可以分为两个学派:频率学派、贝叶斯学派。
1.1 贝叶斯派(主观概率派)
贝叶斯学派用信念的强度(degrees of partial belief)来定义概率。根据这个定义,概率并不是
关于物理系统的,而是关于物理系统和我们之间的关系。也就是说,概率并不是物理世界的本质
属性之一,概率只是人类描述世界的一个工具。
抛一枚硬币有正反两个结果,平时我们认为出现正反两面的概率都是 1/2。但在牛顿经典力学的
框架下,掷硬币的结果是完全决定性的(fully deterministic):硬币和其所在环境的组成的物理
系统在某个时刻的状态是由其前一个时刻的状态决定的。如果我们知道这个系统的初始状态,知
道组成这个系统每一个粒子最开始的速度和位置,原则上通过经典的动态方程,可以计算出这个
系统在之后每一个时刻的状态。
然而,由于我们不知道这个物理系统的全部细节,无法做出精准的预测,只能预测一个大概的结
果,而这个结果就是通过概率的形式来表达的。
再举一个例子:玩扑克牌中的时候,如果对手只剩下两张牌的时候,你要猜测他手里的牌型。你
通过超强的记忆力和精确的演算,推断出他手里的牌是两张单张的可能性稍微大一些(可能性
是 2/3),虽然也有可能是一对(可能性是 1/3),所以你决定接下来打对子。这样的不确定性就
来自于信息的匮乏。因为在对方的眼里,他的牌型是确定性的。要么是单张,要么是一对,非此
即彼,不存在
“2/3
是单张,
1/3
是一对
”
的情况。所以同一个事物的不确定性在不同人的眼里
是不一样的,在缺乏足够信息的情况下,我们虽然能够基于现有的信息进行估计,但是无法推断
出准确的结论;拥有的相关信息越充分,不确定性越低。
根据贝叶斯派,概率代表了我们对于某个事件的信念。如果我们相信这个事件一定会发生,概率
则为 1;如果我们相信这个事件一定不会发生,概率则为 0;如果我们相信这个事件有可能发生,
而测量关于它会发生这个信念的强度就是概率,介于 0 和 1 之间。
但是贝叶斯学派存在难以解释的问题:
1. 如果概率只是对于人们信念强度的测量,那么每个人对于同一个事件会有不同的信念,也
就会给出不同的概率。但是,一般认为像掷硬币这样的事件是存在一个客观的、在不同的
人之间统一的概率。
2. 为什么代表了信念强度的概率满足概率的公理化定义。
1.2 频率学派
频率学派认为概率是物理世界的一个本质属性,不随着人的意志的转移而发生改变。在频率学
派的角度上,概率的测量依靠独立可重复的试验,如果独立可重复试验不断进行下去的话,频率
就会逼近概率,也就是说频率的极限等于概率。
Note: 概率是物理世界的一个本质,也就是说物理世界存在随机,随机的含义就是事物
不被任何东西决定,所以频率派认为概率就是概率,概率就是频率的极限,没有什么更深
层次的原因解释或是决定概率。
频率学派的观点符合量子物理中的一些发现。有些事件是确定性的,比如说如果伽利略松手,铁
球会决定性地砸向比萨斜塔的地面;有些事件则是随机的,比如原子衰变是随机的,这个粒子接
下来可能会衰变,也可能不会,比如说相同的一束所有光子完全一样的光束,在面对与之倾斜的
3
1 概率的本质
偏振片时,一部分光子通过了偏振片,而另一部分光子却没有通过。
但是频率学派确定概率的方式也存在缺陷:
1. 确定一个事件发生的概率需要通过大量重复试验,也就是要求这个事件重复发生,但实际
上,现实中有一些事情不是经常发生的,甚至是无法重复的。例如说,大地震发生的概率,
大地震显然不会经常发生,但我们仍然可以给它定一个概率,又比如说手术的成功的概率,
手术显然不可能重复进行(不会对同一个人进行多次重复手术),显然用频率来确定概率
在这里就会遇到困难。
1.3 总结
如果物理世界可以通过清晰的实体——现象进行二元区分。也就是说,任何事物都有一个 “实
体”,而人类要通过观测这个实体的的现象,来推断实体的性质。贝叶斯派的观点是实体不一定
存在 p 这个参数,参数 p 只是被我们用来研究现象,这就是观察者的角度。而频率派的观点是
参数 p 是存在于实体的,但是我们无法得知,只能通过观测现象去估计参数 p。
实际上,世界是否存在随机,目前可能并没有完全确定的答案,只能说世界存在随机的证据更多
一些。科学史上有不少著名的争论就是源于随机是否是世界本质的讨论。例如爱因斯坦和薛定
谔就非常不喜欢世界存在真正的随机这种观点。所以爱因斯坦说:God does not play dice with
the universe. 而薛定谔提出了“薛定谔的猫”的思想实验。
爱因斯坦这句话的含义是:宇宙中没有真正的随机,这表明了爱因斯坦对量子力学的态度,在世
界观上,爱因斯坦是机械决定论者。
也正是由于以上两种概率的定义方法都有局限性,所以才有人提出了概率的公理化定义。当然,
虽然一般称之为概率的公理化定义,但是这并不是真正意义上的定义。也就是说,被公理化定义
的概率是符合 Kolmogorov 公理要求的事物的集合。公理化系统的目的就是为了避免对概念进
行具体的定义而产生局限性。
1.4 如何理解概率
既然 Kolmogorov 公理不是真正的定义,而频率派和贝叶斯派的观点又各有缺陷性,同时世界是
否存在随机还有争议,那么应该如何理解概率?
实际上,概率完全可以理解为信息量的测度,甚至是对主观倾向的测量。如果我们掌握一个事物
的信息量越多,我们估计出来的概率就越接近真实情况,如果事物确实是随机的,那么我们也确
实估计出来了一个概率。如果事物是确定性的,我们估计出来的概率也可以用于决策(在目前已
有信息量的前提下,我们做出一个正确决策的可能性有多大),当信息量完全的时候,概率就会
为 1 或 0。
很显然,这样的理解完全避开了频率学派和贝叶斯学派的矛盾,虽然看起来是一个无奈之举,但
也是一个巧妙的的方法。
另外,概率的测量存在缺陷:它的对错和准确性非常难以衡量。由于概率并不是对事件本身的直
接测量,因此事件的结果是不能作为直接衡量概率测量准确性的依据的。比如说甲估计 A 事件
发生的概率为 30%,而乙估计 A 事件发生的概率为 60%,最后 A 事件发生了,难道可以说乙的
估计更好吗?因为甲也认为有 30% 的可能性发生 A 事件,这也是可能发生的事件。
这一点和其他理论有很大的区别。比如利用牛顿力学计算一个炮弹的落点,只要让这个炮弹真
的打出去,看看实际落点与理论落点是否吻合即可,两者距离越近,说明计算的准确性越高。
判断概率估计的优劣,必须回到做出概率估计的那个时刻,判断是否是当下最佳的估计。
4

2 测度
2 测度
2.1 幂集
定义2.1 幂集(power set):给定集合 S,S 的所有子集的集合称为 S 的幂集,记为 P (S)(即
P (S) 的元素都是 S 的子集)。用数学语言表示为:P (S) = {U |U ⊆ S}。
2.2 σ 代数
σ 代数(σ 域):给定集合 S,S 的幂集 P (S) 的一个子集称为集合 S 上的 σ 代数。该子集具有
对“差集运算”和“可数个并集运算”的封闭性(因此对于“可数个交集运算”也是封闭的)。σ
代数在测度论中用来定义可测集合,另外在定义条件期望和鞅的时候也需要用到。
σ 代数的数学定义如下:
定义2.2 σ 代数:设 S 为非空集合,F 中的元素是 S 的子集合,满足以下条件的集合族 F 称为
S 上的一个 σ 代数:
1. S 在 F 中
2. 如果一个集合 A 在 F 中,那么它的差集 A
C
也在 F 中
3. 如果有可数个集合 A
1
, A
2
, A
3
, ···, A
n
都在 F 中,它们的并集也在 F 中
Note: 实际上,以上三个条件即是说 F 对 S 的运算具有封闭性。因为,集合交的运算
可以通过并与对立来实现,集合差的运算可以通过对立与交来实现,所以并与对立是集合
最基本的运算。以上第 2 和第 3 个条件正是说了 F 对 S 的对立和并运算封闭。
在测度论中,(S, F) 称为一个可测空间,F 中的某元素,也就是 S 的某子集,称为可测集合。在
概率论中,可测空间写作 (Ω, F),而可测集合被称为随机事件。
2.3 测度
测度(Measure):用一个函数,将某一个集合映射到一个非负数,这个数可以比作大小、体积、
概率等等。测度是一个函数。
传统的积分是在区间上进行的,后来人们希望把积分推广到任意的集合上,就发展出测度的概
念,它在数学分析和概率论有重要的地位,研究对象有 σ 代数、测度、可测函数和积分。
测度的数学定义如下:
定义2.3 测度:一个测度 µ(详细的说法是可列可加的正测度),设集合 F
1
的元素是集合 S 的子
集合,而且是一个 σ 代数,µ 在 F 上定义,值域为 [0, ∞),并且满足以下性质:
1. 空集合的测度为零:µ(∅) = 0
2. 可数可加性,或称 σ 可加性:E
1
, E
2
, ··· 为 P 中可数个两两不相交集合的序列,则所有 E
i
的并集的测度等于每个 E
i
的测度之和,即 µ(
S
∞
i=1
E
i
) =
P
∞
i=1
µ(E
i
)
这三个元素 (S, F, µ) 称为一个测度空间,P 中的某元素称为可测集合。在概率论中,测度空间
写作 (Ω, F, P ),称为概率空间
2
。
1
这里的集合 F 并不一定是指集合 S 的幂集,只是 S 的幂集 P (S) 的子集,P (S) 的子集的元素显然是 S 的子集。
2
概率空间(Ω, F, P ) 是一個总测度为 1 的测度空间(即 P (Ω) = 1)。
5
2 测度
2.4 概率测度
实际上,在概率论中概率并没有具体定义,符合 Kolmogorov 公理的事物被称为概率。
1 Kolmogorov 公理
定一个样本空间 Ω 以及相应的 σ 代数 F,函数 P : P → [0, 1] 若满足:
1. 非负性:对于任意的事件 A,若 A ∈ F,则 P (A) ⩾ 0。
2. 正则性:P (Ω) = 1。
3. 可列可加性:若 A
1
, A
2
, ···, A
n
, ··· 互不相容,则 P (
S
∞
i=1
A
i
) = Σ
∞
i=1
p(A
i
)。
则我们称 P 为概率函数或概率测度。
以上概率的定义通常称之为概率的公理化定义(Axioms of Probability),或者柯尔莫哥洛夫公
理(Kolmogorov Axioms)。
易知,概率测度满足测度的两个性质,概率测度的值域为 [0, 1] ∈ [0, ∞)。概率空间记作 (Ω, F, P )。
Ω 为样本空间,F 为样本空间的某些子集
3
组成的一个事件域(即 σ 域)。
从直观上讲,事件域就是 Ω 中某些子集及其运算(差、对立、并、交)结果而组成的集合类,记
为 F。
F 的定义如下:
设 Ω 为一样本空间,F 为 Ω 的某些子集所组成的集合类,如果 F 满足如下三个条件,则称 F
为一个事件域,又称为 σ 域或者 σ 代数。
1. Ω ∈ F
2. 若 A ∈ F,则
¯
X ∈ F
3. 若 A
n
∈ F, n = 1, 2, ···,则可列并 ∪
∞
n=1
A
n
∈ F
由上面的叙述已经知道测度的实质是一个函数,在概率空间中,该测度函数为概率,概率是一个
函数,满足概率空间三个条件的函数称之为概率。
2.4.1 条件概率
条件概率也属于概率,所以条件概率也满足概率测度的三个性质(条件),即对于条件概率
P (X|Y = y),有:
1. P (X|Y = y) ⩾ 0
2. P (Ω|Y = y) = 1
3. 若 X
1
, X2, ···, X
n
, ··· 互不相容(即 X
i
∩ X
j
̸= ∅, i ̸= j),有 P (
S
∞
i=1
X
i
|Y = y) =
Σ
∞
i=1
p(X
i
|Y = y)。
Note: 在构造条件概率时,我们就使其满足概率测度的要求,但巧妙的是任何一个概率
都可以看作条件概率,例如:P (A) = P (A|Ω)�
3
样本空间的子集并不是总是可测的,尽管在样本空间为可数的情况下定义概率函数相对简单,然而当我们考虑的
样本空间为不可列时,概率函数的定义变得尤为困难。例如当样本空间是实数轴上的一个区间的时候,可以人为地都
构造出无法测量其长度的子集。这样的子集称为不可测集。为了避免这种情况的出现,我们没有必要将连续样本空间
的所有子集都看成是事件,只需要把可测集看成是事件即可(我们只对可以测量的子集感兴趣)。
6

3 概率的公式
2.4.2 Borel 域
若我们关心的样本空间为 Ω = R,我们令 ϕ 为所有开区间的集合:ϕ = {(a, b)| − ∞ < a <
b < +∞},那么包含 ϕ 的最小 σ 代数称为 Borelσ代数 或 Borel 域。其中的元素成为 Borel 集
(Borelset)。
由于 (a, b] =
T
∞
i=1
(a, b +
1
i
),因而所有的左开右闭区间也都是 Borel 集。同理可证所有的左闭右
开区间 [a, b),闭区间 [a, b] 及其可数并、交都为 Borel 集。
2.4.3 勒贝格不可测集
上面有说到不是所有的样本空间的子集都是可测的,这里给出一个例子。
如果我们选取样本空间 Ω = [0 , 1],令 Ω 中的所有有理数集合为 Q
′
,由于有理数为可数集合,因
而可以写成 Q
′
= {q
1
, q
2
, ···}。对于 (0, 1) 之间的任意实数 a,定义集合
S
a
=
a + q if a + q < 1
a + q − 1 if a + q ≥ 1
∀q ∈ Q
′
那么可知 ∪
a∈[0,1]
S
a
= [0, 1]。由于,S
a
也是可数集,因而可以写成 S
a
= {S
a1
, S
a2
, ···}。
令 T
1
为所有 S
a
中的 s
a1
,T
2
为所有 S
a
中的 s
a2
,因而我们有可数个 T
k
,∪
∞
k=1
T
k
= [0, 1],
且 T
k
两两不相交。每个 T
k
地位相等因而 P (T k) = P (T k�)。若 P (T
k
) > 0,则:
1 = P ([0, 1]) = P (∪
∞
k=1
T
k
) = �
∞
k=1
P (T
k
) = ∞
若 P (T
k
) = 0,则:
1 = P ([0, 1]) = P (∪
∞
k=1
T
k
) = �
∞
k=1
P (T
k
) = 0
无论如何都会得到矛盾。
因而在概率论中,在仅仅给定样本空间的情况下,并非任意集合都可以确定其概率。我们一般将
上述性质不够良好的集合称之为(勒贝格)不可测集,而概率空间中 F 应该排除这些性质不够
良好的不可测集。
2.4.4 开集与闭集的概率
3 概率的公式
3.1 加法公式
对于任意 n 个事件 A
1
, A
2
, ··· , A
n
,有
P (
n
[
i=1
A
i
) =
n
X
i=1
P (A
i
)−
X
1≤i≤j≤n
P (A
i
A
j
)+
X
1≤i≤j≤k≤n
P (A
i
A
j
A
k
)+···+(−1)
n−1
P (A
1
A
2
···A
n
)
7
3 概率的公式
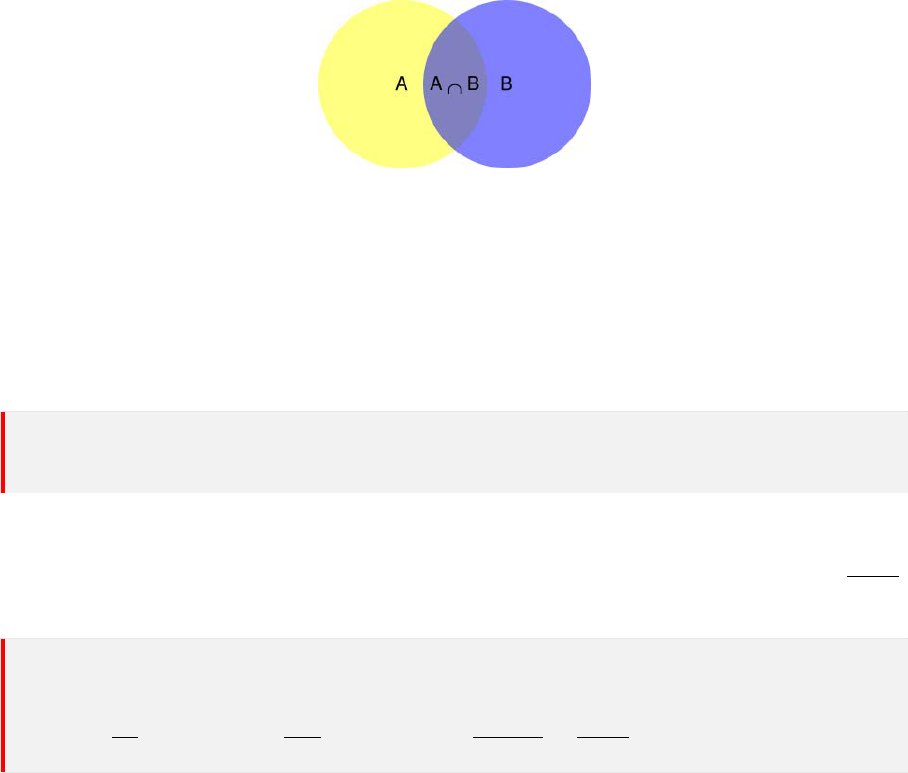
图 1: 条件概率
3.2 乘法公式
3.2.1 条件概率
Note: 乘法公式描述的是多个事件同时发生的概率。相对一般的乘法 A × B,概率论中
也有乘法这个名词,指的就是集合(事件集合)的交的概率。
说到乘法公式,不得不涉及到条件概率。
定义3.1 条件概率:若 A 与 B 是样本空间 Ω 中的两事件,若 P (B) > 0,则 P (A|B) =
P (AB)
P (B)
,
这就是条件概率。P (A|B) 称为 “在 B 发生下,A 的条件概率”。
Note: 为什么条件概率定义为两个概率的比例呢?在第6页中提到,任何概率都可以看作
条件概率。从频率的角度来解释:
P (B) =
N
B
N
Ω
P (AB) =
N
AB
N
Ω
P (A|B) =
N
AB
/N
Ω
N
B
/N
Ω
=
P (AB)
P (B)
也就是,公式中的 P (AB) 是以 P (Ω) 为基础的,P (B) 也是以 P (Ω) 为基础的,而 P (A|B) 则
是以 P (B) 为基础的。但是,这句话是什么意思呢?
要认识到条件概率的意义,必须要引入 “相关” 的概念。我们知道,许多事件是相关的,也就是
一个事件的发生会对另一个事件的发生有影响。从概率论的角度来说,就是一个事件是否发生
会影响另一个事件发生的概率。
举个例子:假设 A�B 事件是相关的,A 事件发生的概率为 P (A),B 事件发生的概率为 P (B)。
现在我们已经知道 A 事件发生了。根据我们先前的经验或研究,我们可以认为若 A 事件发生,
B 事件发生的可能性更大,记 B 事件此时发生的概率为 P (B
1
)。显然,P (B
1
) > P (B),我们已
有的概率 P (B) 已经没有意义,因为 P (B) 无法准确度量此时 B 事件发生的可能性。因此,引
入条件概率。
所以,我们可以知道,条件概率的意义就是对原有概率的修正。这和贝叶斯公式的意义是一样
的,因为接下来所说的贝叶斯公式本质就是一个条件概率。
3.2.2 乘法公式
乘法公式其实就是条件概率的变形,注意到 P (B) = 0 意味着条件概率是没有意义的,这里的没
有意义不仅仅指数学上除数不能为 0,更重要的是我们是不会因为一个概率为 0 的事件而对其
它事件发生的概率进行修正。就算两个事件相关,但是一个事件概率为 0,它又能起到什么影响
呢?
同样的,P (B) 为 0 的话,乘法公式也是没有意义的,虽然作乘法运算的数可以为 0。乘法公式
描述的是两个(多个)事件同时发生的概率,如果其中一个事件发生的概率为 0,那么多个事件
同时发生的概率难道不是 0 吗?
8
3 概率的公式
两事件的简单情形:若 P (B) > 0,则 P (AB) = P (A|B)P (B)
Note: 由条件概率就可以得到。如果 P (B) = 0(事件 B 不会发生),则 P (AB) = 0。
若 P (A
1
A
2
···A
n−1
) > 0,则
P (A
1
···A
n
) = P (A
1
)P (A
2
|A
1
)P (A
3
|A
1
A
2
) ···P (A
n
|A
1
···A
n−1
)
Note: 因为 A
1
⊃ A
1
A
2
⊃ A
1
A
2
A
3
⊃ ..... ⊃ A
1
A
2
...A
n−1
,所以 P (A
1
) ⩾ P (A
1
A
2
) ⩾
P (A
1
A
2
A
3
) ⩾ ..... ⩾ P (A
1
A
2
...A
n−1
) > 0
因此,上式右边的每个条件概率都是有意义的(即不为 0)。
P (A
1
)P (A
2
|A
1
)P (A
3
|A
1
A
2
).....P (A
n
|A
1
A
2
...A
n−1
) = P (A
1
) ·
P (A
1
A
2
)
P (A
1
)
·
P (A
1
A
2
A
3
)
P (A
1
A
2
)
· · ·
·
P (A
1
A
2
....A
n
)
P (A
1
A
2
....A
n−1
)
= P (A
1
, A
2
, ...A
n
)
3.3 全概率公式
描述的是多个交事件的概率。
假设 B
n
: n = 1, 2, 3, ... 是一个概率空间的有限或者可数无限的分割(既 B
n
为一完备事件组
4
),
且每个集合 B
n
是一个可测集合,P (B
i
) > 0,则对任意事件 A 有全概率公式:
P (A) =
X
n
P (A ∩ B
n
)
又因为,根据乘法公式有:P (A ∩ B
n
) = P (A | B
n
)P (B
n
)
此处 P (A|B) 是 B 发生后 A 的条件概率,所以全概率公式又可写作:
P (A) =
X
n
P (A | B
n
)P (B
n
)
3.4 贝叶斯公式
说实话,虽然贝叶斯的公式简单,用乘法公式和全概率公式就可以轻松推导出来,但是我是很久
以后才明白贝叶斯公式的意义。下面先给出贝叶斯公式的定义,相信只看定义和公式证明,很难
想到贝叶斯公式的含义,所以接下来还会给出解释。
在乘法公式和全概率公式的基础上,可建立贝叶斯公式。
【贝叶斯公式】假设 B
n
: n = 1, 2, 3, ... 是一个概率空间的有限或者可数无限的分割(既 B
n
为一
完备事件组),P (A) > 0�P (B
i
) > 0,则
P (B
i
|A) =
P (B
j
)P (A|B
j
)
P
n
i=1
P (B
i
)P (A|B
i
)
证明很简单,运用条件概率定义、乘法公式、全概率公式就可以推导出贝叶斯公式,所以这里就
不写证明过程了。
实际上,贝叶斯公式是一个条件概率,我想这么说应该没什么需要解释的,因为 P (B
i
|A) 就是
条件概率。所以有:
P (B
i
|A) =
P (B
i
A)
P (A)
4
理论上不需要完备也可以,但在实际中,一般认为是完备的。
9

3 概率的公式
条件概率的意义是对原有概率的修正,因此贝叶斯公式的本质也是对原有概率的修正。以上式
为例,就是对 P (B
i
) 的修正。
接下来,我们从贝叶斯公式的本质来推导贝叶斯公式。
∵ P (B|A) =
P (AB)
P (A)
∴ P (AB) = P (B|A)P (A)
同理有,P (AB) = P (A|B)P (B)
∴ P (B|A)P (A) = P (A|B)P (B)
P (B|A) =
P (A|B)P (B)
P (A)
(3.4)
如果,事件 B 可以分成许多个小事件 B
i
,而 B
i
构成了样本空间 Ω 的一个划分(至少)B 包含
A。那么,根据全概率公式有:P (A) =
P
n
P (A | B
n
)P (B
n
)。将这个代入 7 式,就可以得到贝
叶斯公式的一般形式。
对条件概率 3.4 式进行变形,可以得到如下形式:
P (B|A) = P (B)
P (A|B)
P (A)
= P (B)
P (AB)
P (A)P (B)
我们把 P (B) 称为” 先验概率”(Prior probability),即在 A 事件发生之前,我们对 B 事件概率
的一个判断。P (B|A) 称为” 后验概率”(Posterior probability),即在 A 事件发生之后,我们对
B
事件概率的重新评估。
P
(
A
|
B
)/
P
(
A
)
称为
”
可能性函数
”
(
Likely hood
),这是一个调整因子,
使得预估概率更接近真实概率。
所以,贝叶斯公式可以这样理解:后验概率 = 先验概率 x 调整因子
Note: 在这里,如果” 可能性函数”P(A|B)/P(A)>1,意味着” 先验概率” 被增强,事件
B 的发生的可能性变大;如果” 可能性函数”=1,意味着 A 事件无助于判断事件 B 的可能
性;如果” 可能性函数”<1,意味着” 先验概率” 被削弱,事件 B 的可能性变小。
” 可能性函数”=1,也就是意味着 A、B 事件独立,自然 A 事件无助于判断事件 B 的可能
性。
这就是贝叶斯推断的含义。我们先预估一个” 先验概率”,然后加入实验结果,看这个实验到底
是增强还是削弱了” 先验概率”,由此得到更接近事实的” 后验概率”。
通常,事件 A 在事件 B(发生)的条件下的概率,与事件 B 在事件 A(发生)的条件下的概率
是不一样的;然而,这两者是有确定的关系的,贝叶斯定理就是这种关系的陈述。贝叶斯公式的
一个用途在于通过已知的三个概率函数推出第四个。
在贝叶斯公式中,每个名词都有约定俗成的名称:
1. P (A|B) 是已知 B 发生后 A 的条件概率,也由于得自 B 的取值而被称作 A 的后验概率。
2. P (B|A) 是已知 A 发生后 B 的条件概率,也由于得自 A 的取值而被称作 B 的后验概率。
3. P (A) 是 A 的先验概率(或边缘概率)。之所以称为” 先验” 是因为它不考虑任何 B 方面
的因素。
4. P (B) 是 B 的先验概率或边缘概率。
3.5 总结
1. 乘法公式是求单个交事件的概率
2. 全概率公式是求多个个交事件之和的概率
10

4 独立与不相关
3. 贝叶斯公式是求一个逆概率(条件概率)
4 独立与不相关
独立与不相关明显是不同的东西,本质肯定就是它们的定义不同。
4.1 事件的独立性
定义4.1 两个事件的独立性:两个事件 A 和 B 是独立的当且仅当 P (AB) = P (A)P (B)。
实际上,在定义独立性之前,我们先对独立性有一个主观的期待。即,事件 A�B 的独立性是指,
事件 A 的发生,不影响事件 B 的发生。事件 A、B 的独立性是指,事件 A 的发生,不影响事
件 B 的发生。也就是说:若两个事件 A 和 B 是独立的,在 B 发生的条件下 A 发生的条件概
率和 A 的无条件概率一样,即
P (A|B) = P (A)
而根据条件概率的定义,有:
P (A|B) =
P (AB)
P (B)
= P (A)
从而有:
P (AB) = P (A)P (B)
这就是事件 A、B 独立的定义。
定义4.2 多个事件的相互独立:对 n 个事件 A
1
, A
2
, ··· , A
n
, 若下面 2
n
− n −1 个等式同时成立:
P (A
i
A
j
) = P (A
i
)P (A
j
), 1 ≤ i < j ≤ n; 第一部分
P (A
i
A
j
A
k
) = P (A
i
)P (A
j
)P (A
k
), 1 ≤ i < j < k ≤ n;
P (A
i
A
j
A
k
A
l
) = P (A
i
)P (A
j
)P (A
k
)P (A
l
), 1 ≤ i < j < k < l ≤ n;
···············
P (A
1
A
2
···A
n
) = (A
1
)P (A
2
) ···P (A
n
).
第二部分
则称 A
1
, A
2
, ··· , A
n
是相互独立的。
Note: 满足第一部分称为两两独立,两两独立同时满足第二部分则称为相互独立。
显然,对于两个事件来说,两两独立等价于相互独立。但多个事件的相互独立就不能用两
两独立来定义。举个例子,三个事件的相互独立应该定义如下:
对于 3 个事件 A, B, C, 若下面 4 个等式同时成立:
P (AB) = P (A)P (B),
P (AC) = P (A)P (C),
P (BC) = P (B)P (C),
(1)
P (ABC) = P (A)P (B)P (C), (2)
称 A, B, C 相互独立。
11
4 独立与不相关
4.2 试验的独立性
利用事件的独立性定义试验的独立性。
定义4.3 :假如 E
1
的任一结果(事件)、E
2
的任一结果、…、E
n
的任一结果都是相互独立的事
件,则称试验
E
1
、
E
2
、…、
E
n
相互独立。假如这
n
个试验还是相同的,则称其为
n
重独立重
复试验。如果在 n 重独立重复试验中,每次试验的可能结果为两个:A 或
¯
A,则称这种试验为
n 重伯努利试验。
4.3 随机变量的独立性
设 n 维随机变量 (X
1
, X
2
, · · ·X
n
) 的联合分布函数为 F (x
1
, x
2
, · · · , x
n
),随机变量 X
i
的边缘分
布函数为 F
i
(x
i
)。
若对于任意实数 x
1
, x
2
, · · ·x
n
有 F (x
1
, x
2
, · · ·, x
n
) = F
1
(x
1
)F
2
(x
2
) · · · F
n
(x
n
),则称随机变量
X
1
, X
2
, · · ·X
n
是相互独立的。
1. 在离散随机变量场合,如果对其任意 n 个取值 x
1
, x
2
, ···x
n
,有 P (X
1
= x
1
, ···, X
n
= x
n
) =
P (X
1
= x
1
) · · · P (X
n
= x
n
),则称随机变量 X
1
, X
2
, · · ·X
n
是相互独立的。
2. 在连续随机变量场合,如果对其任意 n 个实数 x
1
, x
2
, ···x
n
,有 f(x
1
, x
2
, ···, x
n
) =
n
Π
i=1
f
i
(x
i
),
则称随机变量
X
1
, X
2
,
· · ·
X
n
是相互独立的。
Note: 事件的独立性、试验的独立性、随机变量的独立性,三者的本质都是一样的,都
是基于分布(或者说概率)来定义的。(分布就是概率的描述)
4.4 线性相关性
设 (X, Y ) 是一个二维随机变量。若 E[X −E(X)][Y −E(Y )] 存在,则称它是随机变量 X 与 Y
的协方差,或称为 X 与 Y 的相关(中心)矩,并记为 cov(X, Y ) = E[X −E(X)][Y −E(Y )]。
1. 当 cov(X, Y ) > 0 时,称 X 与 Y 正相关
2. 当 cov(X, Y ) < 0 时,称 X 与 Y 负相关
3. 当 cov(X, Y ) = 0 时,称 X 与 Y 不相关
4.5 不相关与独立的关系
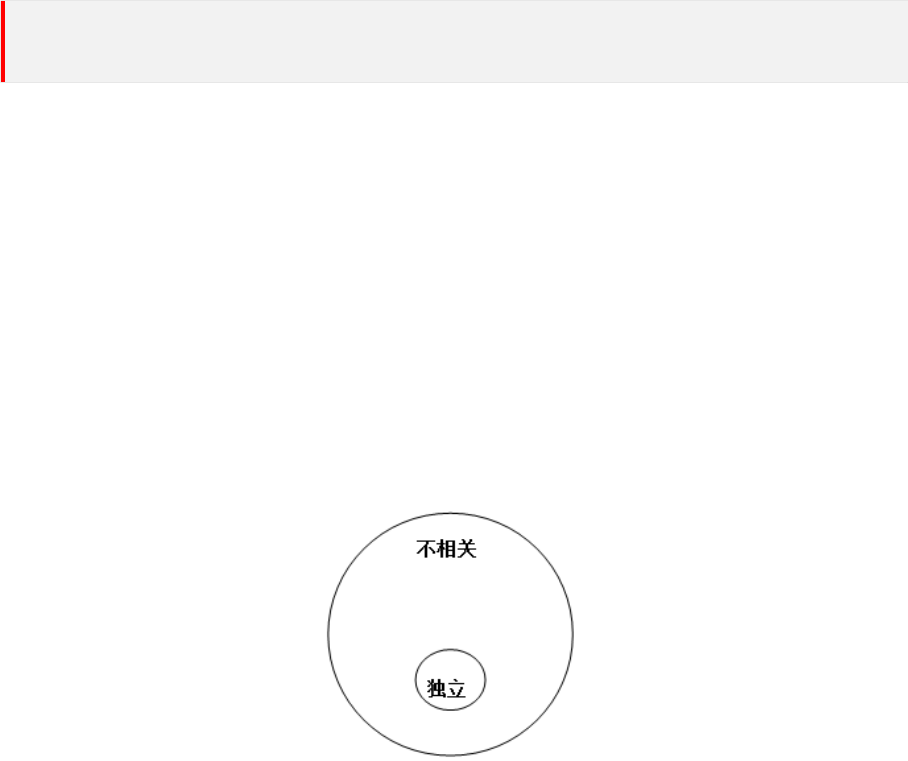
图 2: 不相关与独立
不相关是比独立更弱的概念,因为独立性是用分布定义的,而不相关只是用矩定义的,因此独立
性的要求更严,不相关要求较宽。因此有:
12

4 独立与不相关
若随机变量 X 与 Y 相互独立,则 cov(X, Y ) = 0,反之不成立。
证明.
cov(X, Y ) = E[X − E(X)][Y − E(Y )]
= E{XY − XE(Y ) − Y E(X) + E(X)E(Y )}
= E(XY ) − E(X)E(Y )
因此,若要证明 X�Y 相互独立,其协方差为 0,即证明若 X�Y 相互独立,则 E(XY ) = E(X)E(Y )。
因为 X�Y 相互独立,其联合密度函数与边缘密度函数满足 p(x, y) = p
X
(x)p
Y
(y),同时根据期
望的定义有:
E(XY ) =
+∞
Z
−∞
+∞
Z
−∞
(xy)p
X
(x)p
Y
(y)dxdy
=
+∞
Z
−∞
xp
X
(x)dx
+∞
Z
−∞
yp
Y
(y)dy = E(X)E(Y )
【反例】
设随机变量 X~N(0, σ
2
),且令 Y = X
2
,则 X 与 Y 不独立,此时二者的协方差为 Cov(X, Y ) =
Cov(X , X
2
) = E(X · X
2
) − E(X)E(X
2
) = 0。
13
4 独立与不相关
14
第二部分
基础概率论
15

5 随机变量
5 随机变量
Note: 为了进行定量的数学处理,必须把随机现象的结果数量化,因此需要引进随机变
量。随机变量概念的引进使得对随机现象的处理更加简单和直接。
随机变量是样本空间上的实值函数,由于是随机取值,所以伴随着一个分布。有没有分布是区分
一般变量与随机变量的主要标志。
随机变量用大写字母表示,小写字母表示其取值。
5.1 离散型随机变量
特征是只能取有限个值,或虽则在理论上讲能取无限个值,但这些值可以毫无遗漏地一个接一个
排列出来(可列的)。
5.2 连续型随机变量
变量的全部可能取值无穷多,并且还不能无遗漏地逐一排列,而是充满一个区间。例如秤量一物
体重量的误差,由于我们难于明确指出误差的可能范围,不妨就把它取为 (−∞, ∞) 更方便。又
如电视机的寿命,其范围可取为 (0, ∞),也是一种抽象。
说到底,“连续型变量” 这个概念只是一个数学上的抽象。任何量都有一定单位,都只能在该单
位下量到一定的精度,故必然为离散的。但是当单位极小时,其可能值在一范围内会很密集,不
如视为连续量在数学上更易处理。
6 概率分布
定义6.1 概率分布:是全面地(一个不漏)、动态地描述随机变量取值的概率规律。
6.1 分布函数(概率分布函数)
定义6.2
分布函数:
X
为
r.v.
�
∀
x
∈ R
,称
F
(
x
) =
P
(
X
≤
x
)
为
X
的分布函数,且称
X
服从
F (x),记为 X ∼ F (x)。有时也用 F
X
(x) 以表明是 X 的分布函数。
1. 离散型的分布函数:F (x) =
P
x
i
≤x
p(x
i
)
2. 连续型分布函数:F (x) =
R
x
∞
p(t)dt
F (x) 具有以下三条基本性质(判别分布函数的充要条件):
1. 单调性:F (x) 是一个单调不减的函数,即当 x
1
< x
2
时,F (x
1
) ≤ F (x
2
)。
Note: F (x
2
) − F (x
1
) = P (x
1
< X ≤ x
2
) ≥ 0
2. 有界性:0 ≤ F (x) ≤ 1,且 F (+∞) = lim
x→+∞
F (x) = 1, F (−∞) = lim
x→−∞
F (x) = 0。
证明. 因为 F (x) = P (X ≤ x),即 F (x) 是 X 落在 (−∞, x] 里的概率,所以 0 ≤ F (x) ≤ 1。
由 F (x) 的单调性可以知道,对于任意整数 m 和 n,有 lim
x→−∞
F (x) = lim
m→−∞
F (m)
3. 右连续性:F (x + 0) = lim
x→x
0
+
F (x) = F (x
0
),即 F (x) 是右连续的函数。
17

6 概率分布
Note: 同一样本空间上可以定义不同的随机变量,不同的随机变量可能有不同的分布函
数。
常用公式
P (a < X ≤ b) = F (b) − F (a)
P (X = a) = F (a) − F (a − 0)
P (X ≥ b) = 1 −F (b − 0)
P (X > b) = 1 −F (b)
P (a < X < b) = F (b − 0) − F (a)
P (a ≤ X ≤ b) = F (b) − F (a − 0)
P (a ≤ X < b) = F (b − 0) − F (a − 0)
6.2 分布列
定义6.3 分布列:设 X 是离散的 r.v.,若 X 的所有可能取值是 x
1
, x
2
, ··· , x
n
, ···,则称 X 取 x
i
的概率
p
i
= p(x
i
) = P (X = x
i
), i = 1, 2, ··· , n, ···
为 X 的概率分布列,或简称分布列。
分布列和密度函数一样需要满足非负性和正则性。
6.3 概率密度函数
定义6.4 概率密度: X ∼ F (x),若存在实数轴上的一个非负可积函数 p(x),使得对任意实数 x,
有
F (x) =
Z
x
−∞
p(t)dt
则称 p(x) 为 X 的概率密度函数,简称为密度函数,或称密度。
概率密度函数的基本性质
1. 非负性:p(x) > 0
2. 正则性:
R
∞
−∞
p(x)dx = 1(含有 p(x) 的可积性)
以上两条基本性质是密度函数必须具有的性质,也是确定某个函数能否成为密度函数的充要条
件。
“概率密度” 一词的由来 “密度密数” 这名词的来由可解释如下。取定一个点 X,则按分布函
数的定义,事件 {x < X ≤ x + h} 的概率(h>0 为常数),应为 F (x + h) − F (x)。所以,比
值
F (x+h)−F (x)
h
可以解释为在 x 点附近 h 这么长的区间 (x, x + h) 内,单位长所占有的概率。令
h → ∞ 则这个比的极限,即 F
′
(x) = f(x),也就是在 x 点处 (无穷小区段内)单位长的概率,
或者说,它反映了概率在 X 点处的 “密集程度”。你可以设想一条极细的无穷长的金属杆,总质
量为 1,概率密度相当于杆上各点的质量密度。
18
7 期望
6.4 总结
1. 离散随机变量的分布函数总是右连续的阶梯函数,而连续随机变量的分布函数一定是整个
数轴上的连续函数。前者显然,后者是因为对任意点 x 的增量 ∆x,相应的分布函数的增
量总有 F (x + ∆x) − F (x) =
R
x+∆x
x
p(x)dx −→ 0(∆ → 0)
2. 离散随机变量在其可能取值点上的概率不为 0,而连续随机变量在 (−∞, ∞) 上任一点 a
的概率恒为 0,这是因为 P (X = a) =
R
a
a
p(x)dx = 0。这表明,不可能事件的概率为 0,但
概率为 0 的事件(如 P (X = a) = 0)不一定是不可能事件。类似地,必然事件的概率为
1,但概率为 1 的事件不一定是必然事件。
3. 由于连续随机变量仅取一点的概率恒为 0,从而事件 {a ≤ X ≤ b} 中剔去 x = a 和 x = b,
不影响其概率。
4. 由于在若干点上改变密度函数 p(x) 的值并不影响其积分的值,从而不影响分布函数 F (x)
的值,这意味着一个连续分布的密度函数不唯一。例如
p
1
(x) =
(
1/a , 0 ≤ x ≤ a
0 , else
p
2
(x) =
(
1/a , 0 < x < a
0 , else
但这两个函数在概率意义上是无差别的,在此称 p
1
(x) 与 p
2
(x) 是 “几乎处处相等”,其意
义是:在概率论中可剔去概率为 0 的事件后讨论两个函数相等及其它随机问题。这就是概
率论与微积分的不同之处。
7 期望
定义7.1 期望:根据概率分布,我们以概率值为权重,加权平均所有可能的取值,来获得了该随
机变量的期望 (expectation):
E(x) =
Z
∞
−∞
xp(x)dx
要求
R
∞
−∞
|x|p(x)dx < ∞,即
R
∞
−∞
|x|p(x)dx 收敛。
数学期望在物理上的解释就是重心。概率 p(x
i
) 可看作点 x
i
上的质量密度,F (x) 看作质量在 x
轴上的分布,则 E(X) 就是该质量分布的重心所在的位置。
E(x) 是消除随机性的主要手段,它的本质是常数。
数学期望刻画了 X 的值总在 E(X) 周围波动,但无法反映出波动的大小。
7.1 期望的性质
1. X 是 r.v.,g(x) 是 X 的函数,E[g(x)] =
R
g(x)p(x)dx
2. E(c) = c
3. E(aX) = aE(X)
4. g
1
(x), g
2
(x) 是函数,E[g
1
(X) ± g
2
(X)] = E[g
1
(X)] ± E[g
2
(X)]
8 方差
方差表示分布的离散程度。方差越大,说明随机变量取值范围大。
定义8.1 方差:若随机变量 X
2
的期望 E(X
2
) 存在,则称偏差平方 (X − EX)
2
的数学期望
E(X − EX)
2
为 X 的方差,即:
19
8 方差
V ar(X) = E[(X−µ)
2
] =
Z
+∞
−∞
(x−µ)
2
f(x)dx
Note: 为什么方差存在的必要条件只是 E(X
2
) 存在?
对于所有的随机变量 X,都有 E(X − EX)
2
=
R
x
2
f(x)dx − (EX)
2
。E(X
2
) 存在显然就
是
R
x
2
f(x)dx 存在,同时 E(X
2
) 存在也保证了 E(X) 的存在。
为什么 E(X
2
) 存在也保证了 E(X) 的存在?见下面的证明。
定理
8.1
方差存在,则期望一定存在。
证明. 已知方差存在,即 E(x
2
) 存在,要证明 E(x) 存在。
因为 E(x
2
) 存在,即
R
∞
−∞
x
2
f(x)dx < ∞
又因为 x
2
+ 1 ≥ |x|,所以
R
∞
−∞
(x
2
+ 1)f(x)dx =
R
∞
−∞
x
2
f(x)dx + 1 ≥
R
∞
−∞
|x|f(x)dx
即数学期望存在。
实际上,这是高阶矩存在,低阶矩必存在的特殊情形。
方差的平方根称为标准差 (standard deviation, 简写 std)。常用 σ 表示标准差,X 的标准差记
为 σ(X) 或 σ
X
。
Note: 方差与标准差的区别
方差与标准差的差别主要在量纲上,标准差与随机变量、期望有相同的量纲,所以期望加
减标准差是有意义的。因此标准差更多地被选用。
8.1 方差的性质
1. V ar(X) = E(X
2
) − [E(X)]
2
2. V ar(c) = 0
3. V ar(aX + b) = a
2
V ar(X)
8.2 切比雪夫不等式
标准差(方差)表示分布的离散程度。标准差越大,随机变量取值偏离平均值的可能性越大。可
以计算一个随机变量与期望偏离超过某个量的可能性。比如偏离超过 2 个标准差的可能性。即
P (|X−µ| > 2σ)
定理 8.2. Chebyshev 不等式
对于任意随机变量 X,如果它的期望 EX、方差 V ar(X) 都存在,那么对于任意常数 ε > 0,
有
P (|X−µ| ≥ ε) ≤
σ
2
ε
2
或
P (|X−µ| < ε) ≥ 1 −
σ
2
ε
2
20
8 方差
证明. 设 X 是一个连续随机变量,p(x) 是它的概率密度,期望 EX = a。则:
P (|X − a| ≥ ϵ) =
Z
{X:|X−a|≥ϵ}
p(x)dx ≤
Z
{X:|X−a|≥ϵ}
(X − a)
2
ϵ
2
p(x)dx
≤
1
ϵ
2
Z
∞
−∞
(X − a)
2
p(x)dx
=
σ
2
ϵ
2
Note: 证明过程中用到了两次放大的技巧,第一次放大被积函数,第二次放大积分区域。
只在 |X − a| > ϵ 的区域积分,所以 (X − a)
2
/ε 必定大于 1。
证明第二个不等式会更困难,因此从第一个不等式入手。
在概率论中,事件 {|X −E(X)| ≥ ε} 称为大偏差,其概率 P {|X −E(X)| ≥ ε} 称为大偏差发生
概率。
Chebyshev 不等式给出了大偏差发生概率的上界。这个上界与方差成正比,方差愈大,上界越
大,即:该不等式告诉我们,X 与距离平均值越远,概率就越小。
Chebyshev 不等式让我们摆脱了对分布类型的依赖。
我们知道,方差为 0 意味着随机变量的值集中在一个点上面,而下述定理对此进行了说明。
定理 8.3
若随机变量 X 的方差存在,则 V ar(x) = 0 的充分必要条件是 X 几乎处处为常数,即
P (X = a) = 1 。
证明. 充分性:P (X = a) = 1 −→ V ar(x) = 0
必要性:
因为此时 V ar(X) = 0,所以期望 E(X) 存在。有:
{|X −E(X)| > 0} =
S
∞
n
=1
{|X −E(X)| ≤
1
n
}
P ({|X − E(X)| > 0}) = P (
∞
[
n=1
{|X −E(X)| ≤
1
n
})
=
∞
X
n
=1
(|X −E(X)| ≤
1
n
)
≤
∞
X
n=1
V ar(X)
(1/n)
2
= 0
所以,P ({|X − E(X)| > 0}) = 0,即有 P ({|X − E(X)| = 0}) = 1,即 P (X = E(X)) = 1
21
9 排列组合
9 排列组合
定理 9.1. 分类计数原理(加法原理)
完成一件事,有 n 类方法,第 i 类方式中有 n
i
种不同方法,那么完成这件事总共的方法
数为
X
n
i
定理 9.2. 分步计数原理(乘法原理)
完成一件事,需分成 n 个步骤,做第 i 步有 n
i
种方法,那么完成这件事的方法数为
Y
n
i
Note: 加法原理、乘法原理是数组数学的内容。他们是被证明成立的,并不是公理。这
里不给出证明过程。
注意:加法原理和乘法原理都要求事件之间不相关。
重复排列——有序的重复抽样
如果样本空间总数为 n,抽样 m 次,则总的抽样可能性为
n
m
排列——有序的非重复抽样
有序的非重复抽样又叫做排列 (permutation)。从 n 个样品中挑选 m 个,放入 m 个位置,
总可能性为
P
m
n
= n(n − 1) ···(n − m + 1) =
n!
(n − m)!
重复组合——无序的重复抽样
样本总数为 n 个,抽样 m 次,m 可以大于 n。
重复组合数的得出可以做如下考虑:将 n 个元素画成 n 个盒子,用 n + 1 根火柴棒示意。
如果第 i 个元素取过一次,则在此盒子中用 0 作一记号。
| ⃝ ⃝| |⃝| ······ | ⃝ ⃝ ⃝ |
上图意味着:第一个元素取过 2 次,,第二个元素取过 0 次,第三个元素取过 1 次,……,
第 n 个元素取过 3 次。因为一共取过 m 次,则一共有 m 个 0 和 n+1 个 1。如此,在所
有的 0 和 1 中,除了两端的两个 1 不能动之外,共有 n + m −1 个 0 和 1 可以随意放置。
因此,重复组合相当于在 n + m − 1 个位置任选 m 个位置放置 0,或者在 n + m − 1 个
位置中任选 n − 1 个位置放置 1。
C
n−1
m
+
n
−
1
= C
m
m+n−1
=
(m + n − 1)!
m!(n − 1)!
组合——无序的非重复抽样
无序的非重复抽样又叫做组合 (combination)
C
m
n
=
n(n − 1) ···(n − m + 1)
m!
=
n!
m!(n − m)!
22

10 一维离散分布
10 一维离散分布
10.1 二项分布
设某事件
A
在一次试验中发生的概率为
p
,现把这试验独立地重复
n
次。
A
在这
n
次试验中发
生的次数记为 X,X 可取 0, 1, …, n 等值。
为确定其概率分布,考虑事件 X = k。要这个事件发生,必须在这 n 次试验的原始记录 AA
¯
AA ···
¯
AA
中,有 k 个 A,n − k 个
¯
A。每个 A 有概率 p,而每个
¯
A 有概率 1–p。又因为 n 次试验独立,
即每次 A 出现与否与其它次试验的结果独立。由概率乘法定理给出:每个这样的原始结果序列
发生的概率为 p
k
(1 −p)
n−k
。又因为在 n 个位置中 A 可以占据任何 k 个位置,故一共有 C
k
n
种
可能。由此得出
P (X = k) = C
k
n
p
k
(1 − p)
n−k
k = 0, 1, ···, n
X 所遵从的概率分布称为二项分布,记为 B(n, p)。
Note:
1. 事件 A 在一次试验中发生的概率为 p,这个概率是不变的,也就是要求每次实验的
条件是稳定的。
2. 各次试验是独立的。
10.1.1 期望与方差的推导
P
(
X
=
k
) =
C
k
n
p
k
q
n−k
, k = 0 , 1, ··· , n; q = 1 − p
EX =
n
X
k=0
kC
k
n
p
k
q
n−k
=
n
X
k=1
kC
k
n
p
k
q
n−k
=
n
X
k=1
k
n!
k!(n − k)!
p
k
q
n−k
= np
n
X
k=1
k
(n − 1)!
(k − 1)!(n − k)!
p
k−1
q
(n−1)−(k−1)
= np
n
X
k=1
C
k−1
n−1
p
k−1
q
(n−1)−(k−1)
= np
C
0
n−1
p
0
q
n−1
+ C
1
n−1
p
1
q
n−2
+ ... + C
n−1
n−1
p
n−1
q
0
= np
∵ DX = EX
2
− (EX)
2
EX
2
=
n
X
k=1
k
2
n
k
p
k
q
n−k
, k = 0 , 1, ··· , n; q = 1 −p
=
n
X
k=1
k(k − 1) + k
n
k
p
k
q
n−k
23

10 一维离散分布
=
n
X
k=1
k(k − 1)
n
k
p
k
q
n−k
+
n
X
k=1
k
n
k
p
k
q
n−k
其中,
P
n
k=1
k
n
k
p
k
q
n−k
= EX = np
n
X
k=1
k(k − 1)
n
k
p
k
q
n−k
=
n
X
k=1
k(k − 1)
n!
k!(n − k)!
p
2
p
k−2
q
n−k
=
n
X
k=2
k(k − 1)
n!
k!(n − k)!
p
2
p
k−2
q
n−k
注:特别注意这里 k=1 时项为 0,所以可以从 k=2 开始计算。
上式 =
n
X
k=2
n(n − 1)(n − 2)!
(k − 2)!(n − k)!
p
2
p
k−2
q
[(n−2)−(k−2)]
= n(n − 1)p
2
n
X
k=2
(n − 2)!
(k − 2)!(n − k)!
p
k−2
q
[(n−2)−(k−2)]
= n(n − 1)p
2
n
X
k=2
n − 2
k − 2
p
k−2
q
[(n−2)−(k−2)]
= n(n − 1)p
2
∴ EX
2
= n(n − 1)p
2
+ np
∴ DX = EX
2
− (EX)
2
= np − np
2
= np(1 − p)
Note: 推导过程关键是利用二项式 [p + (1 − p)]
n
= 1,为了能利用该二项展开式需要掌
握凑的技巧,即把 k 提出去,凑成二项展开式的形式。而且要注意到,即使求和时 k 不从
0 开始,二项展开式也是从 0 次幂开始的。
10.1.2 二项分布期望与方差的简单推导
上面介绍了直接推导二项分布期望、方差的方法,如果借助二项分布的可加性(当然,二项分布
的可加性我们还没有叙述),很容易看出二项分布的期望与方差。
二项分布 X ∼ B(n, p) 中 X 表示的是 n 次伯努利试验中事件发生次数。用随机变量 X
i
表示
第 i 次伯努利试验的结果,那么 n 次伯努利试验总的随机变量 X 可以表示成:X = X
1
+ X
2
+
... + X
i
+ ... + X
n
。
根据均值和方差的性质,如果两个随机变量 X、Y 相互独立,那么:
E(X + Y ) = E(X) + E(Y )
D(X + Y ) = D(X) + D(Y )
对于二项分布 X ∼ B(n, p),每一次伯努利试验都相互独立,因此:
E(X) = E(X
1
) + E(X
2
) + ··· + E(X
n
) = p + p + ··· + p = np
D(X) = D(X
1
) + D(X
2
) + ··· + D(X
n
) = p(1 − p) + p(1 − p) + ··· + p(1 −p) = np(1 − p)
显然,负二项分布的期望与方差也能通过这种方式推导出来。
24

10 一维离散分布
10.1.3 名字由来
因为 C
i
n
p(1 − p)
n−i
恰好是二项式 (p + (1 − p))
n
展开式中的第 k+1 项。
实际生活中有许多现象程度不同地符合这些条件,而不一定分厘不差。例如,某厂每天生产 n 个
产品,若原材料质量、机器设备、工人操作水平等在一段时期内大体保持稳定,且每件产品之合
格与否与其他产品合格与否并无显著关联,则每日的废品数 X 大体上服从二项分布。
又如一大批产品 N 个,其废品率为 p,从其中逐一抽取产品检验其是否废品,共抽 n 个。若每
次抽出检验后又放回且保证了每次抽取时,每次每个产品有同等的
1
N
的机会被抽出,则这 n 个
产品中所含废品数
X
就相当理想地遵从二项分布了。反之,如果每抽出一个检验后即不放回去,
则 下一次抽取时,废品率已起了变化,这时 X 就不再服从二项分布了。但是,若 N 远大于 n,
则即使不放回,对废品率影响也极小,这时,X 仍可近似地作为二项分布来处理。
10.2 伯努利分布(0 − 1 分布)
伯努利分布 (Bernoulli distribution) 是很简单的离散分布。在伯努利分布下,随机变量只有两个
可能的取值:1 和 0。随机变量取值 1 的概率为 p。相应地,随机变量取值 0 的概率为 1 − p。
很显然,伯努利分布是二项分布的特例。n = 1 时的二项分布称为伯努利分布。其分布列为
p(X = k) = p
k
(1 − p)
1−k
, k = 1, 0
10.3 泊松分布
法国数学家 poisson 在 1837 年首次提出泊松分布。
泊松分布 (Poisson distribution) 是二项分布的一种极限情况,当 成功概率p→0, 试验次数n→+∞
而 np = λ 时,二项分布趋近于泊松分布。这意味着我们进行无限多次试验,每次成功概率无穷
小,但 n 和 p 的乘积是一个有限的数值。Poisson 分布起源于 Poisson 对二项分布的极限研究。
二项分布是离散型机率模型中最有名的一个,其次是 Poisson 分布。Poisson 分布大多用于描述
一定的时间或空间内出现的事件个数。
通过下面的例子来阐释泊松分布产生的机制。
10.3.1 推导泊松分布
设有一段时间被我们所观察,同时设这段时间为 [0, 1),取一个很大的自然数 n,把时间 [0, 1) 分
成等长的 n 份。即:l
1
[0,
1
n
), l
2
[
1
n
,
2
n
), ··· , l
n
[n − 1, 1)。
作几个假定:
1. 在每段 l
i
内,恰发生一个 A 事件的概率近似地与这段时长
1
n
成正比,即可以取为 λ
1
n
。
2. 又假定 n 很大,所以
1
n
很小,以至于在 l
i
这么短的时间内发生两次 A 事件的概率几乎为
0。因此,在每段 l
i
内不发生 A 事件的概率为 1 − λ
1
n
。
3. 每段 l
i
是否发生 A 事件是独立的。
按照上述假定,[0, 1) 内发生的 A 事件数 X 服从二项分布,于是
P (X = k) = C
k
n
(
λ
n
)
k
(1 −
λ
n
)
n
−
k
很显然,上式只是近似成立而非严格等式。但是,当 n → ∞ 的时候,就会严格成立。当 n → ∞
时,有
C
k
n
n
k
→
1
k!
,(1 −
λ
n
)
n
→ e
−λ
。因此,可以知道 P (X = k) = C
k
n
(
λ
n
)
k
(1 −
λ
n
)
n−i
的极限为
25

10 一维离散分布
i
k!
e
−k
。这被称为泊松定理,推导过程入下:
由上面的叙述可知推导的已知条件有:
1. p =
λ
n
,也就是 λ = np
2. n → ∞
lim
n→∞
P (X = k) = lim
n→∞
n
k
p
k
(1 − p)
n−k
= lim
n→∞
n!
(n − k)!k!
λ
n
k
1 −
λ
n
n−k
= lim
n→∞
n!
n
k
(n − k)!
| {z }
F
λ
k
k!
1 −
λ
n
n
| {z }
→exp(−λ)
1 −
λ
n
−k
| {z }
→1
= lim
n→∞
1 −
1
n
1 −
2
n
. . .
1 −
k − 1
n
| {z }
→1(一共 k 项相乘)
λ
k
k!
1 −
λ
n
n
| {z }
→exp(−λ)
1 −
λ
n
−k
| {z }
→1
=
λ
k
k!
exp (−λ)
lim
n→∞
1
−
λ
n
n
= e
−λ
lim
n→∞
(1 −
λ
n
)
n
= lim
n→∞
[(1 +
1
n
−λ
)
n
−λ
]
−λ
= e
−λ
lim
n→∞
n!
n
k
(n − k)!
= lim
n→∞
n(n − 1)(n − 2) ···(n − k + 1)
n
k
= 1
综上所述,泊松分布的分布列为:
P (X = k) =
λ
k
k!
e
−λ
一般地说,若 X ∼ B(n�p),其中 n 很大,p 很小而 np = 不太大时,则 X 的分布接近于泊松
分布 P ()。这个事实在所述条件下,可将较难计算的二项分布转化为泊松分布去计算。
10.3.2 泊松分布期望和方差的推导
求 EX
when k = 0, k ·
λ
k
e
−λ
k!
= 0
∴ E(X) =
∞
X
k=1
k ·
λ
k
e
−λ
k!
E(X) =
∞
X
k=1
k ·
λ
k
e
−λ
k!
=
∞
X
k=1
λ
k
e
−λ
(k − 1)!
=
∞
X
k=1
λ
k−1
λe
−λ
(k − 1)!
= λe
−λ
∞
X
k=1
λ
k−1
(k − 1)!
in T aylor series, e
x
= 1 + x +
x
2
2!
+
x
3
3!
+ ... +
x
n
n!
+ ... =
∞
X
k=1
x
k−1
(k − 1)!
∴ E(X) = λe
−λ
∞
X
k=1
λ
k−1
(k − 1)!
= λe
−λ
e
λ
= λ
求 DX
26

10 一维离散分布
E(X
2
) =
∞
X
k=0
k
2
·
λ
k
e
−λ
k!
= λe
−λ
∞
X
k=1
kλ
k−1
(k − 1)!
= λe
−λ
∞
X
k=1
(k − 1 + 1)λ
k−1
(k − 1)!
= λe
−λ
(
∞
X
m=0
m · λ
m
m!
+
∞
X
m=0
λ
m
m!
)(m = k − 1)
= λe
−λ
(λ ·
∞
X
m=1
λ
m−1
(m − 1)!
+
∞
X
m=0
λ
m
m!
)
= λe
−λ
(λe
λ
+ e
λ
)
= λ(λ + 1)
∴ D(X) = E(X
2
) − (E(X))
2
= λ(λ + 1) − λ
2
= λ
Note:
1. 位于均值 λ 附近概率较大。
2. 随着 λ 的增大,分布逐渐趋于对称。
10.3.3 poisson 分布的由来
5
poisson 分布由 Simeon D. Poisson 最先得到。Simeon D. Poisson(1781~1840 年)是一个著名
的法国数学家及物理学家。到了晚年,他热衷于将数学的机率论用到司法的运作上。他在这方面
的主要著作是 1837 年出版的《司法机率的研究》(Recherches sur la Probabilité des Jugements)。
虽然这本书的主旨是要对司法运作有具体的贡献,但它包含了许多纯粹数学的、机率的理论,所
以可以看成是一本以司法应用为例的机率课本,这本书德文版的书名《机率论及其重要应用》看
起来和内容较为一致。在这本书的数学推演中,Poisson 从二项分布的极限得到了这个日后以他
为名的概率分布。
Poisson 虽然得到这样的机率分布,但在书中他并没有继续讨论这种分布的性质,在往后的研究
中,Poisson 似乎也把它忘掉了。
Poisson 分布虽然出于 Poisson 之手,但真正使它为人重视,使它成为统计学一部分的却是
Bortkiewicz。
直到十九世纪末,Bortkiewicz 才注意到 Poisson 分布与某些数据之间也有类似的关联。他写了
一本小册子《小数法则》(Das Gesetz der Kleinen Zahlen),专门研究 Poisson 分布。他不但在
理论方面推演了 Poisson 分布的许多性质,并且在应用方面,也比较了一些实际发生的、有关于
自杀或意外伤害的数据。
10.4 超几何分布
一批产品共 N 个,其中废品 M 个。现从中随机 取出 n 个,问 “其中恰好 m 个废品” 这个事件
A 的概率是多少?
以 X 记从 N 个产品中随机抽出 n 个里面含废品数。按该例的计算,X 的分布为
5
引用自曹亮吉《Poisson 分布》
27

10 一维离散分布
P (X = m) =
C
m
M
C
n−m
N−M
C
n
N
, 0 ≤ m ≤ M, 0 ≤ n − m ≤ N − M
该分布称为超几何分布,是因为其形式与 “超几何函数” 的级数展式的系数有关。
这个分布在涉及抽样的问题中常用,特别当 N 不大时。因为通常在抽样时,多是像在本例中这
样 “无放回的”,即已抽出的个体不再有放回去以供再次抽出的机会,这就与把 n 个同时抽出的
效果一样。如果一个一个地抽而抽出过的仍放回,结果是二项分布。若
n
N
很小,则放回与不放
回差别不大。由此可见,在这种情况下超几何分布应与二项分布很接近。确切地说,若 X 服从
超几何分布,则当 n 固定,
M
N
= p 固定,N → ∞ 时,X 近似地服从二项分布。
10.4.1 超几何分布的期望和方差
准备公式:C
0
n
C
k
m
+ C
1
n
C
k−1
m
+ C
2
n
C
k−2
m
+ ··· + C
k
n
C
0
m
= C
k
n+m
; n, m, k ∈ N
∗
; k ≤ n, k ≤ m
利用恒等式 (1 + x)
n+m
= (1 + x)
n
(1 + x)
m
的二项展开式的系数相等便可以证明上式。
EX=
m
X
k=0
k
C
k
M
C
n−k
N−M
C
n
N
=
m
X
k=1
C
k−1
M
C
n−k
N−M
C
n
N
=
M
C
n
N
m
X
k=1
C
k−1
M−1
C
n−k
N−M
=
M
C
n
N
C
m−1
N−1
= n
M
N
EX
2
=
m
X
k=0
k
2
C
k
M
C
n−k
N−M
C
n
N
=
m
X
k=1
k
2
C
k
M
C
n−k
N−M
C
n
N
=
m
X
k=2
k(k − 1)
C
k
M
C
n−k
N−M
C
n
N
+ n
M
N
=
M(M − 1)
C
n
N
m
X
k=2
C
k−2
M−2
C
n−k
N−M
+ n
M
N
=
M(M − 1)
C
n
N
C
n−2
N−2
+ n
M
N
=
M(M − 1)n(n − 1)
N(N − 1)
+ n
M
N
DX = EX
2
− (EX)
2
=
nM(N − M )(N − n)
N
2
(N − 1)
10.5 负二项分布(帕斯卡分布)
为了检查某厂产品的废品率大小,有两个试验方案可采取:
1. 从该厂产品中抽出若干个,检查其中的废品数 X,这一方案导致二项分布。
2. 先指定一个自然数 r,一个一个地从该厂产品中抽样检查,直到发现第 r 个废品为止。以
28

10 一维离散分布
X 记到当时为止已检出的合格品个数。显然,若废品率 p 小,则 X 倾向于取较大之值,反
之当,p 大时,则 X 倾向于取小值。故 X 可用于考究 p。这一方案导致负二项分布。
为计算 X 的分布,假定每次抽取的结果(是废品或否)时独立的,且每次抽得废品的概率保持
固定,为 p。考察 X=i 这个事件,为使这个事件发生,需要以下两个事件同时发生:
1. 在前 i − 1 次抽取中,恰有 r − 1 个废品
2. 第 i 次抽取出废品
这两个事件的概率分别为 b(r − 1; i − 1; p) 和 p。因为这两个事件是独立的,两事件同时发生的
概率等于两事件的概率乘积。
P (X = i)= b(r − 1; i + r −1; p) ∗ p
= C
r−1
i−1
p
r−1
(1 − p)
i−r
∗ p
= C
r−1
i−1
p
r
(1 − p)
i−r
由几何分布的无记忆性,负二项分布实际可以看做 r 个几何分布之和:X = X
1
+X
2
+···+X
r
∼
Nb(r, p),其中诸 X
i
∼ Ge(p) 独立同分布。
10.5.1 名字由来
由于负指数二项展开式
(1 − x)
−r
=
∞
X
i=0
C
i
−r
(−x)
i
=
∞
X
i=0
C
i
i+r−1
x
i
=
∞
X
i=0
C
r−1
i+r−1
x
i
令 x = 1 − p,并令两边乘以 p
r
,得
1 = p
r
[1 − (1 − p)]
−r
=
∞
X
i=0
C
r−1
i+r−1
p
r
(1 − p)
i
这就验证了密度函数的非负性和正则性。另外,也由于例中所描述的试验方式,它与二项分布比
是 “反其道而行之”;二项分布是定下总抽样个数 n 而把废品个数 X 作为变量;负二分布则相
反,它定下废品个数 r 而把总抽样次数减去 r 作为变量。
10.6 几何分布
特别地,当 r = 1 时,负二项分布变为
P (X = i) = p(1 −p)
i
必定在最后一次抽出废品(成功),而前面的都是正常品,所以排序只有一种。
几何分布具有无记忆性,这是由于每次试验都是独立的试验,不受之前试验结果的影响。因为几
何分布描述的是第一次成功发生在第 X 次的概率,而几何分布基于伯努利试验,伯努利试验的
概率是稳定的。
10.6.1 几何分布的期望和方差
EX =
∞
X
k=1
kpq
k−1
= p
∞
X
k=1
kq
k−1
= p
∞
X
k=1
dq
k
dq
= p
d
dq
(
∞
X
k=0
q
k
) = p
d
dq
(
1
1 − q
) =
p
(1 − q)
2
=
1
p
29

11 各一维离散分布的联系
E(X
2
) =
+∞
X
k=1
k
2
pq
k−1
= p[
+∞
X
k=1
k(k − 1)q
k−1
+
+∞
X
k=1
kq
k−1
]
= pq
+∞
X
k=1
k(k − 1)q
k−2
+
1
p
= pq
+∞
X
k=1
d
2
q
k
dq
2
+
1
p
= pq
d
2
dq
2
(
+∞
X
k=0
q
k
) +
1
p
= pq
d
2
dq
2
(
1
1 − q
) +
1
p
= pq
2
(1 − q)
3
+
1
p
=
2q
p
2
+
1
p
V ar(X) = E(X
2
) − (EX)
2
=
2q
p
2
+
1
p
−
1
p
2
=
1 − p
p
2
推导二项分布的期望与方差的时候,利用了二项式定理,而这里利用了求导(求导和求和交换次
序)和拆项(k+1-1)。
10.6.2 几何分布的无记忆性
定理 10.1. 几何分布的无记忆性
X ∼ Ge (p),则对任意的正整数 m, n,有 P (X > m + n|X > m) = P (X > n)。
即:在前 m 次未出现 A 的情形下,接下来 n 次试验中仍未出现 A 的概率只与 n 有关而与 m
无关。
证明. 用条件期望公式和等比数列求和公式即可证明。
几何分布的无记忆性可与负二项分布作对比。
10.6.3 名字由来
概率 p, p(1 − p), p(1 − p)
2
, ··· 呈公比作为 1 − p 的几何级数。
11 各一维离散分布的联系
二项分布、几何分布、负二项分布都是基于独立的伯努利试验。
二项分布:描述在给定的 n 次试验中成功 X 次的概率;描述有限总体的放回抽样问题,或者无
限总体的抽样问题。
超几何分布:描述有限总体的无放回抽样问题。
泊松分布:二项分布的特例,描述在某个单位内(如:单位时间、单位面积、单位产品······)
上,事件的具体发生概率。
几何分布:描述第一次成功发生在第 X 次的概率,也就是描述首次成功所需试验次数的概率分
布情况。
负二项分布:描述第 r 次成功发生在第 x 次的概率,也就是描述成功 r 次,所需的试验次数的
概率分布情况。
30

12 一维连续分布
11.1 总结
1. 几何分布是 r = 1 的负二项分布特例。
2. 伯努利分布是二项分布 n = 1 时的特例。
3. 独立的伯努利分布的随机变量之和服从二项分布。
4. 独立的几何分布的随机变量之和服从负二项分布。
5. 泊松分布是二项分布 n → ∞ 时的特例。
12 一维连续分布
12.1 正态分布(Gauss 分布)
高斯在研究误差理论的时候,首先用正态分布来刻画误差的分布。
对于具有以下密度函数的随机变量 X,我们称其服从正态分布 (Normal Distribution)(或高
斯分布 (Gauss Distribution)),记作 X ∼ N (µ, σ
2
)。
p(x) =
1
σ
√
2π
e
−
(x−µ)
2
2σ
2
正态分布具有以下性质:
1. 期望 µ,方差 σ
2
2. p(x) 是关于 x = µ 对称的一条钟形曲线,在对称轴处达到最大值。µ ± σ 是曲线的拐点
3. 如果固定 σ 只改变 µ,p(x) 图形仅作平移而形状不变,因此称 µ 为位置参数
4. 如果固定 µ 只改变 σ,p(x) 图形分布的集中程度改变(σ 越大,图形越 “矮胖”),称 σ 为
尺度参数
5. 3σ 原则:绝大部分的值落在 µ±3σ 的范围内(这是根据正态分布函数算出来的,而不是切
比雪夫不等式)
P (|X − µ| < kσ) =
0.6826, k = 1 ,
0.9545, k = 2 ,
0.9973, k = 3 .
12.1.1 标准正态分布
将 N(0, 1) 称为标准正态分布 (Standard Normal Distribution),其密度函数记为 (x),分布
函数记为 (x)。
标准化:如果 X ∼ N(µ, σ),那么 U =
X−µ
σ
∼ N(0, 1)
12.1.2 正态分布的期望和方差
E(X) =
Z
+∞
−∞
x ·
1
√
2πσ
e
−
(x−µ)
2
2σ
2
dx
=
1
√
2πσ
Z
+∞
−∞
(x − µ)e
−
(x−µ)
2
2σ
2
dx +
1
√
2πσ
Z
+∞
−∞
µe
−
(x−µ)
2
2σ
2
dx
=
1
√
2πσ
Z
+∞
−∞
te
−
t
2
2σ
2
dt + µ
Z
+∞
−∞
1
√
2πσ
e
−
(x−µ)
2
2σ
2
dx
31

12 一维连续分布
= 0 + µ
= µ
12.2 均匀分布
若随机变量 X 的密度函数为以下 p(x):
p(x) =
1
b − a
, a < x < b,
0, otherwise.
, F (x) =
0, x < a,
x − a
b − a
, a ≤ x < b,
1, x ≥ b.
那么称 X 服从区间 (a, b ) 上的均匀分布 (Uniform Distribution),记作 X�U (a, b)。其分布函
数如上述的 F (x)。其期望是区间中点 EX =
a+b
2
,方差为 V ar(X) =
(b−a)
2
2
。
12.2.1 名字的由来
均匀分布这个名称的来由很明显。因为密度函数 f 在区间 [a�b] 上为常数,故在这区间上,概率
在各处的密集程度一样。或者说,概率均匀地分布在这区间上。
12.3 指数分布与其无记忆性
X 服从指数分布 (Exponential Distribution),记为 X�Exp():
p(x) =
(
λe
−λx
, x ≥ 0,
0, x < 0.
, F (x) =
(
1 − e
−λx
, x ≥ 0,
0, x < 0.
其期望
EX
=
1
λ
,方差 V ar(X) =
1
λ
2
。指数分布是非负的,因此常常被用作元件寿命的分布;在
可靠性与排队论中也有应用。
其他性质:
1. 指数分布的无记忆性:P (X > s + t|X > s) = P (X > t),很容易证明。
2. 泊松分布与指数分布的关系:例如,在时段 [0, t] 内某机器故障的次数 N (t)�P (t),那么连
续两次故障之间的时间间隔 T �Exp()。
指数分布常用来作各种 “寿命” 分布的近似【所有不是由于自身的原因、自身的磨损、
自身的损耗(或者自身的损耗很慢)而引起的损坏,即损坏由意外引起的东西的寿命
服从指数分布】,如某些电子元件的寿命服从指数分布。
统计学中常称指数分布为 “永远年青” 的分布。
12.3.1 负指数一词的由来
�>0,x>0。e
−λx
总为负值,由于这个原因,指数分布也称为负指数分布。
12.4 Weibull 分布
若考虑老化,则应取失效率随时间而上升,不能为常数,而应 取为一个 x 的增函数,例如 λx
m
,
对某个常数 λ > 0, m > 0,在这个 条件下,按上例的推理,将得出:寿命分布 F (x) 满足微分方
程 F
′
(x)/[1 − F (x)] = λx
m
,此与初始条件 F (0) = 0 结合,得出
32

12 一维连续分布
F (x) = 1 −e
−(λ/m+1)x
m+1
取 a = m + 1(a > 1),并把 λ/(m + 1) 记为 λ,得出
F (x) = 1 −e
−λx
a
, x > 0
而 F (x) = 0 当 x < 0,此分布之密度函数为
f(x) =
(
λax
a−1
e
−λx
a
, x > 0
0 , x ≤ 0
上两式分别称为威布尔分布函数和威布尔密度函数。它 与指数分布一样,在可靠性统计分析中
占重要的地位。实际上指数分布是威布尔分布当 a = 1 时的特例。
12.5 伽马分布
X 服从伽马分布 (Gamma Distribution),记为 X�Ga(α, λ):
p(x) =
(
λ
α
Γ(α)
x
α−1
e
−λx
, x ≥ 0,
0, x < 0.
其中 Γ(α) =
R
∞
0
x
α−1
e
−x
dx, α > 0,称为伽马函数。伽马函数有如下的性质:
1. Γ(1) = 1, Γ(
1
2
) =
√
π
2. Γ(α + 1) = αΓ(α)
3. 当 n 为自然数时,有:Γ(n + 1) = nΓ(n) = n!
当 α = 1 时,e
−x
就是参数 λ = 1 的指数分布,所以显然 Γ(1) = 1。
12.5.1 伽马分布的性质
1. 期望 EX =
α
λ
,方差 V ar(X) =
α
λ
2
2. 当 0 < α�1,密度函数是严格下降的;当 1 < α �2,密度函数是先上凸后下凸的单峰函数;
当 α > 2,密度函数仍单峰,先下凸、再上凸、最后下凸
3. � 越大,它越接近正态分布;但它始终是偏峰函数
12.5.2 伽马分布的两个特例
• 当 = 1 时,伽马分布就是指数分布;
• 当 α = n/2, λ = 1/2 时,伽马分布是自由度为 n 的卡方分布 (Chi-square Distri-
bution),记为 X�2(n)。这里 n 可以是任意正实数,但通常取正整数。其期望与方差:
EX = n, V ar(X) = 2n
12.6 贝塔分布
Be(a, b) =
Γ(a + b)
Γ(a)Γ(b)
x
a−1
(1 − x)
b−1
, 0 < x < 1
期望 EX =
a
a+b
,方差
ab
(a+b)
2
(a+b+1)
。
33
13 随机变量函数的分布
13 随机变量函数的分布
离散随机变量在分布列的基础上直接计算即可,以下主要讨论连续随机变量。
对于连续型的随机变量,有两种方法:
1. 分布函数法
2. 定理法
13.1 分布函数法
直接由 Y 的分布函数 F
Y
(y) = P (g(X) ≤ y) 出发,按函数 g(x) 的特点作个案处理。
13.1.1 步骤
已知 X ∼ p
X
(x),要求 Y = f(X) 的分布密度 P
Y
(y)
1. 先求分布函数:F
Y
(y) = P (Y ≤ y) = P (f(X) ≤ y) = P (X ∈ C
y
) =
R
C
y
p
X
(x)dx,其中
C
y
= {x|f(x) ≤ y}。
2. 再求密度函数:p
Y
(y) = F
′
Y
(y) =
dF
Y
(y)
dy
下面直接给出一个例子来说明 “分布函数法” 的应用。
【例题】设 X ∼ exp(1),求 Y = X
2
的概率密度。
解:X ∼ p
X
(x) =
(
e
−x
x > 0
0 else
当 y > 0
F
Y
(y) = P (Y ≤ y) = P (X
2
≤ y) = P (−
√
y ≤ X ≤
√
y) =
R
√
y
−
√
y
p
X
(x)dx =
R
√
y
0
e
−x
dx
从而 p
Y
(y) = F
′
Y
(y) = (
R
√
y
0
e
−x
dx)
′
= e
−
√
y
·
1
2
√
y
所以 p
Y
(y) =
(
e
−
√
y
2
√
y
y > 0
0 else
13.2 定理法
定理 13.1
设 X 是连续随机变量,其密度函数为 p
X
(x),Y = g(X) 是另一个随机变量,若 y = g(x)
严格单调,其反函数 h(y) 有连续导数,则 Y = g(X) 的密度函数为
p
Y
(y) =
(
p
X
[h(y)] · |h
′
(y)|, a < y < b
0, otherwise.
其中 a = min{g(−∞), g(+∞)}, b = max{g(−∞), g(+∞)}
推断13.1 设 X ∼ p
X
(x), Y = kX + b,则 Y :
1
|k|
p
X
(
y−b
k
)(直接运用定理即可)
【总结】
34
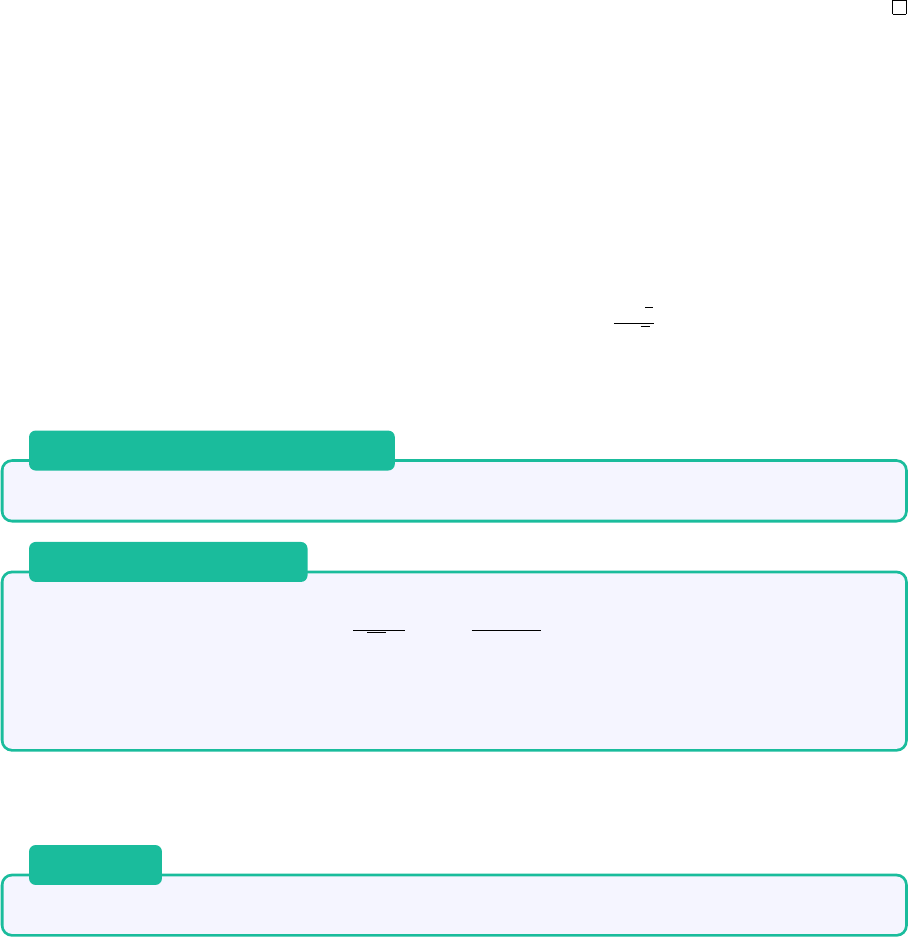
13 随机变量函数的分布
1. 只要 y = f(x) 在 p
X
(x) 中 x 起作用的区间内单调,就可用定理法
2. pY (y) 中 y 的范围由
(
y = f(x)
p
X
(x)中 x 起作用段
共同决定
给出如下证明,证明过程不难:
证明. 不妨设 y = g(x) 严格单调增加,则它的反函数 x = h(y) 存在,且也严格单调增加。因为
Y = g(X) 在区间
α = g(−∞), β = g(+∞)
之间取值
所以当 y ≤ α 时, F
Y
(y) = P (Y ≤ y) = 0
当 y ≥ β 时,F
Y
(y) = P (Y ≤ y) = 1
当 α < y < β 时,F
Y
(y) = P (Y ≤ y) = P (g(X) ≤ y) = P (X ≤ h(y)) =
R
h(y)
−∞
p
X
(x)dx
于是,Y 的概率密度函数为
p
Y
(y) =
(
p
X
[h(y)]h
′
(y) a < y < b
0 else
g(x) 严格单调减函数的情形可以类似证明。但要注意的是,此时 h
′
(y) < 0,因此需要加上绝对
值符号,这时 (α = g(∞), β = g(−∞))。
沿用上述例题来说明上述定理的应用。
【例题】设 X ∼ exp(1),求 Y = X
2
的概率密度。
解:X ∼ p
X
(x) =
e
−x
x > 0
0 else
当 x > 0 时,函数 y = x
2
单调递增,由定理
p
Y
(y) =
p
X
(h(y)) |h
′
(y)| α < y < β
0 else
=
(
e
−
√
y
2
√
y
y > 0
0 else
利用定理13.1,可以证明以下定理。
定理 13.2. 正态变量的线性不变性
随机变量 X ∼ N(µ, σ
2
),则当 a ̸= 0 时,有 Y = aX + b ∼ N (aµ + b, a
2
σ
2
)。
定理 13.3. 对数正态分布
随机变量 X N (µ, σ
2
),则 Y = e
x
的概率密度函数为
P
Y
(y) =
(
1
√
2πyσ
exp{−
(lny−µ)
2
2σ
2
} , y > 0
0 , y ≤ 0
且 Y 称服从对数正态分布,记为 Y ∼ LN
µ, σ
2
,其中 µ 称为对数均值,σ
2
称为对数
方差。
对数正态分布是偏态分布,也是一个常用分布。例如:绝缘体材料的寿命、设备故障的维修时间、
家中仅有两个小孩的年龄差从夫对数正态分布。
定理 13.4
随机变量 X ∼ Ga(α, λ),则当 k > 0 时,有 Y = kX ∼ Ga(α, λ/k)。
35
14 分布的其它特征数
定理 13.5
随机变量 X 的分布函数 F
X
(x) 是严格单调的连续函数,其反函数 F
−1
X
(x) 存在,则 Y =
F
X
(X) 服从 [0, 1] 上的均匀分布。
证明. 求 Y 的分布函数就是求 F
X
(X) 的分布函数。因为 F
X
(X) 仅在 [0, 1] 上面取值,所以
当 y < 0 时
F
Y
(y) = P (Y ≤ y) = P (F
X
(X) ≤ y) = 0
当 0 ≤ y ≤ 1 时
F
Y
(y) = P (Y ≤ y) = P (F
X
(X) ≤ y) = P (X ≤ F
−1
X
(y)) = F
X
(F
−1
X
(y)) = y
当 1 < y 时,F
Y
(y) = 1
Note: 该定理表明均匀分布在连续分布类中占有特殊地位,因为任意一个连续随机变量
都可以通过其分布函数与均匀分布发生关系。
利用该推论,可以通过生成均匀分布随机数的方法生成一些其他分布的随机数。
14 分布的其它特征数
14.1 k 阶矩
定义14.1 k 阶矩:对于正整数 k 与随机变量 X,如果以下数学期望都存在,则有:
原点矩 (Raw moment):µ
k
= E(X
k
)
中心矩 (Central moment):v
k
= E
(X −EX)
k
标准矩 (Standardized moment):ˆµ
k
=
µ
k
[V ar(X)]
k/2
对以上整数 k 的情形,统称为 k 阶矩 (k-th moment)。
定理 14.1
高阶矩存在,则低阶矩必定存在。
证明. 通过定义的方法证明:
k 阶矩 E|X|
k
就是积分
R
|X|
k
dP ,当 k + 1 阶矩存在时,k 阶矩这个积分可以分为 |X| > 1 和
|X| ≤ 1 两部分分别积分然后加起来,前一部分积分 ≤ |X|
(
k+1) 的积分,因为 |X|
k
<= |X|
(
k+1)
(当 |X| > 1 时),后一部分积分 ≤ 1,所以加起来仍然是有限的。也就是 |X|
k−1
≤ |X|
k
+ 1
因此 k + 1 阶矩有限意味着 k 阶矩有限。
Note: 在概率论中,矩的本质是期望,期望存在要求级数绝对收敛,而 |X|
k−1
≤ |X|
k
+ 1
即意味着,若高阶矩存在,那么高阶级数一定绝对收敛,低阶级数小于高阶级数,则低阶
级数也收敛。
36

14 分布的其它特征数
14.1.1 中心矩与原点矩的关系
中心矩与原点矩的关系:
v
k
= E(X − µ
1
)
k
=
k
X
i=0
k
i
µ
i
(−µ
1
)
k−i
因此有:
v
1
= 0
v
2
= µ
2
− µ
2
1
v
3
= µ
3
− 3µ
2
µ
1
+ 2µ
3
1
14.2 变异系数(离散系数)
变异系数也称为离散系数 (coecient of variation),它是一组数据的标准差与其相应的平均数之
比。
若随机变量 X 的二阶矩存在,则 X 的变异系数为:
C
v
(X) =
p
V ar(X)
E(X)
=
σ(X)
E(X)
方差和标准差反映了数据离散程度,用方差或标准差去比较两个随机变量的离散程度的时候,会
有两个问题:
1. 方差或标准差数值的大小受原变量值自身水平高低的影响,也就是与变量的平均数大小有
关,变量值绝对水平高的,离散程度的测度值自然也就大,绝对水平低的离散程度的测度
值自然也就小
2. 方差或标准差与原变量值的计量单位相同,采用不同计量单位计量的变量值,其离散程度
的测度值也就不同。
因此,对于平均水平不同或计量单位不同的不同组别的变量值,是不能用标准差直接比较其离散
程度的。为消除变量值水平高低和计量单位不同对离散程度测度值的影响,需要引进变异系数。
显然变异系数是一个无量纲的量,因为标准差与期望的量纲是一致的,两者的量纲相抵消。
14.3 分位数
设 X F (x),密度函数为 p(x),对任意 p ∈ (0, 1),称满足下述条件的 x
p
为此分布的分位数,又
称为下侧 p 分位数。
F (x
p
) =
Z
x
p
−∞
p(x)dx = p
同理,我们称满足下述条件的 x
′
p
为此分布的上侧分位数。
1 − F (x
′
p
) =
Z
−∞
x
′
p
p(x)dx = p
下侧分位与上侧分位数可以相互转换
x
′
p
= x
1−p
x
p
= x
′
1−p
37

15 参考文献
14.4 中位数
X F (x),p = 0.5 时的 p 分位数 x
0.5
是 F (x) 的中位数。
F (x
0.5
) =
Z
x
0.5
−∞
p(x)dx = 0.5
14.5 偏度
偏度是随机变量 X 的三阶标准矩,用于描述分布偏离对称性。如果随机变量 X 的前三阶矩存
在,则比值:
β
s
=
v
3
v
3
2
2
=
E(X − EX)
3
[V ar(X)]
3/2
= E
"
X −EX
SD(X)
3
#
称为 X 的偏度系数,简称偏度 (Skewness)。偏度值大于 0 时称为正偏或右偏 (right-skewed),
小于零时称为负偏或左偏 (left-skewed)。
14.6 峰度
峰度是随机变量 X 的四阶标准矩,用于描述分布尖峭程度与(或)尾部粗细。如果随机变量 X
的前四阶矩存在,则:
β
k
=
v
4
v
2
2
− 3 =
E(X − EX)
4
[V ar(X)]
2
称为 X 的峰度系数,简称峰度 (Kurtosis),有时也记作 Kurt[X]。峰度值大于 0 表示分布比
标准正态分布更尖峭、尾部更粗;小于 0 表示比标准正态分布更平坦、尾部更细。
15 参考文献
[1] 茆诗松,程依明,濮晓龙. 概率论与数理统计教程(第二版). 高等教育出版社. 2010
[2] 陈希孺. 概率论与数理统计. 中国科学技术大学出版社.2009
[3] 贾俊平,何晓群,金勇进. 统计学(第六版). 中国人民大学出版社. 2014
38
第三部分
概率论进阶
39

16 随机变量序列的四种收敛
16 随机变量序列的四种收敛
定义16.1 弱收敛 (convergence in distribution):设置随机变量 X, X
1
, X
2
, ··· 的分布函数分
别为 F (x), F
1
(x), F
2
(x), ···。若对 F (x) 的任一连续点 x,都有
lim
n→∞
F
n
(x) = F (x)
则称 {F
n
(x)} 弱收敛于 F (x),记作 F
n
(x)
W
→ F (x)。也称 {X
n
} 按分布收敛于 X,记作 X
n
d
→ X。
Note: 也就是说,当 n 很大的时候,X
n
的累积函数和 X 的累积函数(的取值)无限接
近。直观上而言,依分布收敛只在乎随机变量的分布,而不在乎他们之间的相互关系。
举一个例子:倘若已知 X
n
d
→ X,假设 Y = −X。对于任意一个发生的事件,Y 与 X 的取值正好
反号。但这并不影响 X 与 Y 有相同的累积分布函数,即 F
X
(z) = F
Y
(z)。如此一来,X
n
d
→ Y 。
更一般的情况而言,只要 X 与 Y 有相同的累计函数,即 same distributed,即使 P (X = Y ) < 1,
也有 X
n
d
→ Y 。因为依分布收敛仅仅在乎分布,而不在乎相互之间的关系。
定义16.2 依概率收敛 (convergence in probability):设 {X
n
} 为一随机变量序列,X 为一随
机变量,如果对任意 ∀ε > 0 有
lim
n→∞
P (|X
n
− X| ≥ ε) → 0
则称 {X
n
} 依概率收敛于 X,记作 X
n
P
→ X。
Note: 也就是说,当 n 很大的时候,对任意发生的事件,X
n
的值和 X 的值不相等的概
率趋向 0,但 |X
n
−X| 依然有概率取比较大的值。直观上而言,依概率收敛在乎的是随机
变量的值。
这样说来,前面依分布收敛的例子如果套在概率收敛上就会出现问题。如果 X
n
d
→ Y ,但对于任
何一个与 X 分布一样的 Y ,P (X = Y ) < 1 不一定成立,因为 X 与 Y 只是分布相同,而值不
同。但反而言之,如果 X
n
P
→ X,即它们的值都差不多了,那么它们的分布一定也差不多,即
X
n
d
→ X。因此,依概率收敛比依分布收敛要强,即 X
n
P
→ X ⇒ X
n
d
→ X。
但在某种情况下,取值就可以确定分布。即 X 取某个常数的情况下(退化分布)。此时 X 的取
值和 X 的分布唯一确定。即此时会有依分布收敛和依概率收敛等价,即 X
n
P
→ X ⇔ X
n
d
→ X。
定义16.3 几乎必然收敛 (convergence almost surely):随机变量序列 {X
n
} 几乎必然收敛收
敛于随机变量 X,即 X
n
as
→ X,当且仅当
P ( lim
n→∞
|X
n
–X| < ε) = 1
其中 ε 为任意正实数。
Note: 依概率收敛、几乎必然收敛的区别
依概率收敛要求随着 n 的增大 X
n
与 X 不相等的概率越来越小,即 X
n
出现其他值的概
率越来越小,极限为 0。
而几乎必然收敛则是要求,存在 N,当 n > N 时,X
n
= X 必须成立。
即依概率收敛限制尾部概率收敛至 0,而几乎必然收敛限制尾部概率等于 0。
定义16.4 Lp 收敛 (convergence in Lp):随机变量序列 {X
n
} 依 Lp 收敛于随机变量 X,即
X
n
L
p
→ X,当且仅当
41

17 大数定律
E(X
n
− X)
p
→ 0 , n → ∞ p ≥ 1
当 p = 2 时称为均方收敛。
直观上而言,均方收敛在乎的也是随机变量的值,但要求比依概率收敛更严格,因为根据切比雪
夫不等式,概率测度被均方限制。由切比雪夫不等式:
P (|X − µ| ≥ ε) ≤
E(X − µ)
2
ε
2
因此,X
n
L
2
→ X ⇒ X
n
P
→ X。
总结
1. 几乎处处收敛和 Lp 收敛最强,依概率收敛其次,依分布收敛最弱。
2. 几乎处处收敛和 Lp 收敛并无推导关系。
3. 在收敛到常数时,依概率收敛和依分布收敛等价。
4. 比几乎处处收敛更强的是数学分析中的完全收敛。
17 大数定律
17.1 伯努利大数定律
伯努利大数定律是研究这种极限定理的第一个定律,也是一个从理论上证明随机现象的频率具
有稳定性的定律。
定理 17.1. 伯努利大数定律
设 µ
n
是 n 重伯努利试验中事件 A 出现的次数,而 p 是事件 A 在每次试验中出现的概
率,则对任意 ε > 0,都有
lim P
n→∞
{|
µ
n
n
− p| < ε} = 1
定理的含义:µ
n
是 n 重伯努利试验中 A 出现的次数,则
µ
n
n
便是这 n 次试验中 A 出现的频率,
上式表明,当次数 n 很大时,事件 A 出现的频率与事件 A 出现的概率 p 的偏差超过任意正数
的可能性很小,或者基本上说,是不可能的。
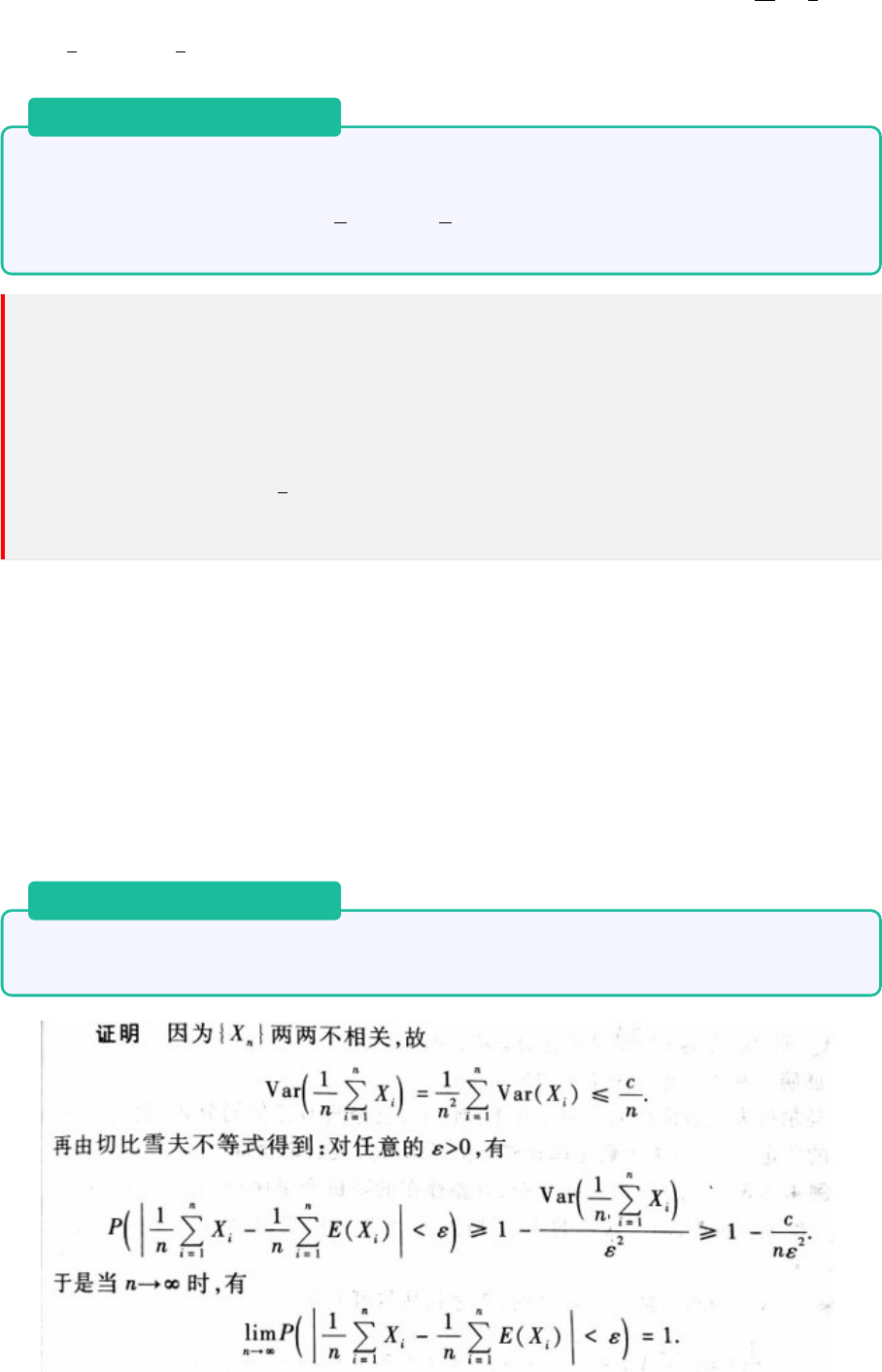
证明.
E(
µ
n
n
) = E(
1
n
n
X
i=1
X
i
) =
1
n
n
X
i=1
E(X
i
) = p
D
(
µ
n
n
) =
D
(
1
n
n
X
i=1
X
i
) =
1
n
2
n
X
i=1
D
(
X
i
) =
pq
n
由切贝雪夫不等式有:P {|
µ
n
n
− p| ≥ ε} ≤
D(
µ
n
n
)
ε
2
=
pq
nε
2
当 n → ∞,
pq
nε
2
→ 0,因此 lim P {|
µ
n
n
− p| ≥ ε} = 0,亦即 lim
n→∞
P {|
µ
n
n
− p| < ε} = 1。
伯努利大数定律证明了在大量重复的伯努利试验中,随机事件的频率在它的概率的附近摆动,若
事件的概率很小,则事件的频率也很小,或者说事件很少发生。
伯努利大数定律还提供了通过试验来确定事件概率的方法。既然频率
µ
n
n
与概率
p
有较大偏差
的可能性很小,那么就可以通过做试验确定某事件发生的频率并把它作为相应概率的估计。这
是参数估计的内容,参数估计是数理统计中主要的研究课题之一。参数估计的一个重要理论基
础就是大数定律。
42
17 大数定律
17.2 大数定律一般形式
在伯努利大数定律的形式下,可推广出大数定律的一般形式。在伯努利大数定律中:
µ
n
n
=
1
n
n
P
i=1
X
i
,
p = E(
1
n
n
P
i=1
X
i
) =
1
n
E(
n
P
i=1
X
i
),因此有:
定理 17.2. 大数定律一般形式
设有一随机变量序列 {X
n
},假如它具有形如下式的性质,则称该随机变量序列 {X
n
} 服
从大数定律:∀ε > 0
lim
n→+∞
P {
1
n
n
X
i=1
X
i
−
1
n
n
X
i=1
E(X
i
)
< ε} = 1
Note: 也就是
lim
n→+∞
P {
¯
X − µ
< ε} = 1
大数定律的本质就是样本均值依概率收敛于期望。
独立同分布随机变量序列 {X
n
} 服从大数定律是依概率收敛的特殊情况。构造另外一个随
机序列 {Y
n
},其中,Y =
1
n
n
P
i=1
E(X
i
) = µ,则 {X
n
} 服从大数定律等价于 Y
n
P
→µ。依概
率收敛是把原收敛于一个常数 µ 推广到收敛于一个随机变量场合。
大数定理有两种用法:
1. 当样本足够多的时候,样本均值和分布均值足够接近的概率非常大
2. 当样本足够多的时候,可以用样本均值来近似分布均值。
问题来了,随机变量序列 {X
n
} 在什么条件下满足定理 17.2呢?以下的大数定律的差别就是在
条件上。
17.3 切比雪夫大数定律
定理 17.3. 切比雪夫大数定律
设 {X
n
} 为一列两两不相关的随机变量序列,若每个 X
i
的方差存在,且有共同的上界,
即 V ar(X
i
) ≤ c, i = 1, 2, ···,则 {X
n
} 服从大数定律。
43

17 大数定律
17.4 马尔可夫大数定律
马尔可夫条件:
1
n
2
V ar(
n
X
i=1
X
i
) → 0
定理 17.4. 马尔可夫大数定律
对随机变量序列 {X
n
},若马尔可夫条件成立,则 {X
n
} 服从大数定律。
该定理的条件中没有任何同分布、独立性、不相关的假定。
17.5 辛钦大数定律
定理 17.5. 辛钦大数定律
设 {X
n
} 为一独立同分布的随机变量序列,若 X
i
的数学期望存在,则 {X
n
} 服从大数定
律。
注意:该定理提供了求随机变量数学期望 E(X) 的近似值方法。
17.6 总结
定律 分布情况 期望 方差 结论
辛钦大数定律 独立同分布 存在 — 估算期望
马尔可夫大数定律 — — 马尔可夫条件 估算期望
切比雪夫大数定律 两两不相关 — 存在,上界相同 估算期望
伯努利大数定律 二点分布 相同 相同 频率 = 概率
马尔可夫大数定律、切比雪夫大数定律虽然没有写明要求随机变量的期望存在,但是要求方差存
在。而方差存在,则期望必定存在。
伯努利大数定律是切比雪夫大数定律和辛钦大数定律的特例,切比雪夫大数定律是马尔可夫大
数定律的特例。
44
18 中心极限定理
18 中心极限定理
中心极限定理,有两个版本,一个针对独立同分布的样本,一个针对独立不同分布的样本。
18.1 独立同分布下的中心极限定理
定理 18.1. 林德贝格-莱维中心极限定理
设随机变量序列 {X
n
} 是相互独立, 服从同一分布的,且有 E(X
i
) = µ, V ar(X
i
) = σ
2
> 0,
记
Y
∗
n
=
X
1
+ X
2
+ ··· + X
n
− nµ
σ
√
n
则对任意实数 y 有
lim
n→+∞
P (Y
∗
n
≤ y) = Φ(y) =
1
√
2π
Z
y
−∞
e
−
t
2
2
dt
18.2 二项分布的正态近似
定理 18.2. 棣莫弗-拉普拉斯极限定理
设 n 重伯努利试验中,事件 A 在每次试验中出现的概率为 p(0 < p < 1),记 µ
n
为 n 次
试验中事件 A 出现次数,且记 Y
∗
n
=
µ
n
−np
√
npq
,则对任意实数 y 有
lim
n→+∞
P (Y
∗
n
≤ y) = Φ(y) =
1
√
2π
Z
y
−∞
e
−
t
2
2
dt
Note: 由于离散和连续的区别,用正态作为二项分布的近似计算中,一般先作如下修正
后再用正态近似 P (k
1
≤ µ
n
≤ k
2
)=P (k
1
− 0.5 < µ
n
< k
2
+ 0.5)
若记 β = Φ(y),则由棣莫弗-拉普拉斯极限定理给出的近似式:P (Y
∗
n
≤ y) ≈ Φ(y) = β 可用来
解决三类计算问题:
1. 已知 n, y,求 β
2. 已知 n, β,求 y
3. 已知 y, β,求 n
18.3 独立不同分布下的中心极限定理
【林德贝格条件】设 {X
n
} 是一个独立的随机变量序列,它们具有有限的数学期望和方差:E(X
i
) =
µ
i
,V ar(X
i
) = σ
2
i
, i = 1, 2, ···,设 X
i
为连续随机变量,其密度函数为 p
i
(x),若对任意的 τ > 0,
有
lim
n→+∞
1
τ
2
B
2
n
n
X
i=1
Z
|X−µ
i
|>τB
n
(x−µ
i
)
2
p
i
(x)dx = 0
则称 {X
n
} 满足林德贝格条件。
45

18 中心极限定理
定理 18.3. 林德贝格中心极限定理
设独随机变量序列 {X
n
} 满足林德贝格条件,则对任意的 x,有
lim
n→+∞
P {
1
B
n
n
X
i=1
(X
i
− µ
i
) ≤ x} =
1
√
2π
Z
x
−∞
e
−t
2
/2
dt
注意:如果独立随机变量序列 {X
n
} 具有同分布和方差有限的条件,则必定满足林德贝格条件,
也就是说定理 4.4.1 是定理 4.4.3 的特例。
定理 18.4. 李雅普诺夫中心极限定理
设 {X
n
} 为独立随机变量序列,若存在 δ > 0,满足 lim
n→+∞
1
B
2+δ
n
n
P
i=1
E(|X
i
− µ
i
|
2+δ
} = 0,
则对任意的 x,有
lim
n→+∞
P {
1
B
n
n
X
i=1
(X
i
− µ
i
) ≤ x} =
1
√
2π
Z
x
−∞
e
−t
2
/2
dt
其中 µ
i
与 B
n
如前所述。
46
第四部分
数理统计
47
19 抽样分布
19 抽样分布
19.1 统计学分布
在概率论中,我们接触到了一些常见的分布。在数理统计中,我们也会经常接触到分布,主要是
抽样分布。注意,数理统计所说的分布和概率论中的分布不是同一个概念。
概率论
正态分布
二项分布
泊松分布
数理统计
总体分布
样本分布
抽样分布
定义19.1 总体分布:总体中各元素的现测值所形成的相对頻数分布,称为总体分布(population
distribution)。
如果总体中的所有观测值都能得到,我们就可以通过直方图来观察它的分布状况。但现实中,几
乎得不到总体的所有观测值,因而有必要进行抽样推断。总体的分布往往是不知道的。通常是根
据经验大致了解总体的分布类型,或者可以假定它服从某种分布。
我们所关心的主要是总体的一些参数,如均值、比例、方差等。只要知道了样本统计量的抽样分
布,就可以推断这些参数。
定义19.2 经验分布:从总体中抽取一个容量为 n 的样本,由这 n 个观测值形成的相对频数分布,
称为样本分布(sample distribution)。
Note: 由于样本是从总体中抽取的,其中包含着总体的一些信息和特征,因此样本分布
也称经验分布。
定义19.3 经验分布函数:设 x
1
, x
2
, . . . , x
n
是取自总体分布函数为 F (x) 的样本,若将样本观测
值由小到大进行排列,为 x
(1)
, x
(2)
, . . . , x
(n)
,则称 x
(1)
, x
(2)
, . . . , x
(n)
为有序样本,用有序样本定
义如下函数
F
n
(x) =
0, x<x
(1)
k/n, x
(k)
≤ x < x
(k+1)
, k = 1, 2, ..., n − 1
1, x
(n)
≤ x
则 F
n
(x) 是一非减右连续函数,且满足 F
n
(−∞) = 0 和 F
n
(+∞) = 1,由此可见,F
n
(x) 是一
个分布函数,并称 F
n
(x) 为经验分布函数。
定理 19.1. 格里纹科定理(Glivenko–Cantelli theorem)
设 x
1
, x
2
, . . . , x
n
是取自总体分布函数为 F (x) 的样本,F
n
(x) 是其经验分布函数,当 n → ∞
时,有 P {su p |F
n
(x) − F (x)| → 0} = 1
Note: 格里纹科定理表明:当 n 相当大时,经验分布函数是总体分布函数 F (x) 的一个
良好的近似。经典的统计学中一切统计推断都以样本为依据,其理由就在于此。
虽然当样本容量 n 逐渐增大时,样本的分布逐渐接近总体的分布。但由于样本是随机抽取的,当
样本容量很小时,样本的分布就有可能与总体的分布不一致,或许会有较大的差异。
注意的是,样本分布是指一个样本中各观测值的分布,而抽样分布是样本函数(统计量)的分布。
定义19.4 统计量: x
1
, x
2
, . . . , x
n
为取自某总体的样本,若样本函数 T = T (x
1
, x
2
, . . . , x
n
) 中不
含有任何未知参数。则称 T 为统计量。
49

19 抽样分布
定义19.5 抽样分布:统计量的分布称为抽样分布。
Note: 简而言之,统计量是以样本为自变量,关于总体的不含未知参数的函数。注意,虽
然统计量不依赖未知参数,但其分布依赖于未知参数。
常用的统计量有样本均值、样本方差、样本矩。
19.2 抽样分布的作用
如果要理解抽样分布的神奇,那就要看看它的作用是什么,而它的作用就体现于参数与统计量的
联系之中。
统计量是样本的函数,是样本特征的概括性度量(数字特征),比如
¯
X、S 等等。而参数是总体
特征的概括性度量,比如:µ、σ 等等。看起来统计量和参数是一组配对的概念,这理解并没有
错,但是我们还是要清楚这两者的区别与联系。
共同点
• 它们都是某一事物特征的概括性度量
区别
• 统计量是样本的函数(随机变量);参数并不是函数,而是和总体有关的一个常数
Note: 统计量是样本的函数,但这里所说的函数并不是数学分析中的函数,而是概率论
中的函数——随机变量。
函数的自变量可以是确定性的,也可以是随机的。
▷ 确定性是指自变量的取值由我们任意给定,我们可以确定自变量的取值
▷ 随机是指自变量的取值是随机的
我们一般接触的函数的自变量是确定性的,数学分析中的函数基本如此,但概率论中的函
数——随机变量则不是这样。我们知道随机变量的本质就是实值函数,将随机事件的结果
映射为实数,由于事件的随机性,导致函数自变量
a
具有随机性。自然,如果自变量取值具
有随机性,因变量的取值也会随机。
a
自变量来自样本空间 Ω
之所以说统计量是样本的函数是因为:样本统计量的值却完全依赖于所抽取的样本,比如,不同
的样本就会有不同的样本均值。但参数并不是函数,参数是和总体有关系的一个常数,这个常数
客观存在,尽管我们不知道。统计量存在的意义就是用于推断总体参数,这就是两者的联系。
因为统计量函数,它会随着样本的变化而变化,所以根据样本统计量来推断总体的参数必然具
有不确定性。那么,应如何判断用样本统计量来推断总体参数时的可靠性呢?这就需要抽样分布
了,抽样分布包含统计量的某种确定的性质,而这些性质是已知的,而且反映在抽样分布之中。
因此,抽样分布提供了相关统计量长远而稳定的信息,它构成了推断总体参数的理论基础。
上面这段话摘录自某本统计学入门教材,是不是有点似懂非懂的感觉呢?什么是统计量的某种
确定的性质?我的理解是是这样的,抽样分布与总体参数有关系,同时抽样分布又是统计量的分
布,这就将统计量与参数联系到了一起,因此可以用统计量推断参数。一般而言,抽样分布的参
数涉及总体参数,这就是统计量的分布包含未知参数的原因。因此,使用统计量推断参数的理论
依据就是统计量的分布的参数涉及总体参数。(见第50页)也正是因此,抽样分布是参数估计、
假设检验、方差分析等内容的理论基础。
50
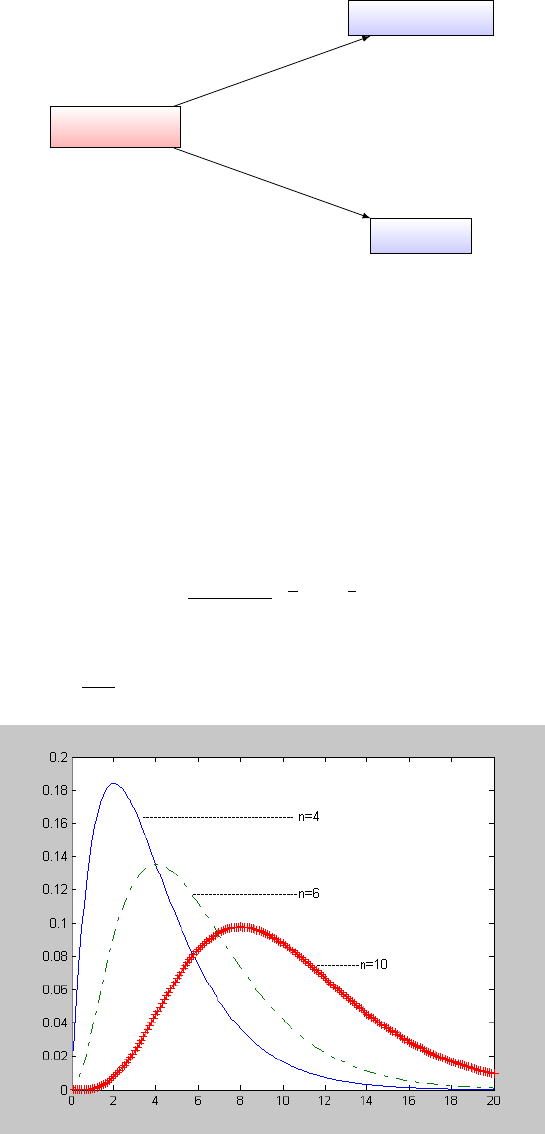
19 抽样分布
19.3 三大抽样分布
如上一节所述,统计量是我们对总体的分布函数或数字特征进行统计推断的最重要的工具,所以
寻求统计量的分布成为数理统计的基本问题之一。
抽样分布可以分为精确的抽样分布和渐进分布。至于为什么这么分类,顾名思义就可以得到答
案。至今已求出的精确抽样分布并不多,因为精确的抽样分布通常很难求,有时候尽管求出了精
确抽样分布,但也因为过于复杂而难以应用。相对来说,极限分布更容易求,而在样本量较大时,
我们就可以用统计量的极限分布来近似它的精确抽样分布,这就是渐进分布。
例如:中心极限定理说的就是样本均值
¯
X 的渐进分布 (极限分布) 是正态分布。
抽样分布
渐进分布
大样本问题中使用
精确抽样分布
小样本问题中使用
还算幸运的是,大多总体都服从正态分布:而基于正态分布的总体,我们可以求出一些重要统计
量的精确分布,例如以下所说的三大抽样分布:χ
2
分布、t 分布、F 分布。
19.3.1 χ
2
分布
χ
2
分布由 Hermert 和皮尔逊分别在 1875 和 1900 年推导出来。
定义19.6 χ
2
分布:设 X
1
, X
2
, . . . . . . , X
n
独立同分布于标准正态分布 N(0, 1),则 χ
2
= X
2
1
+
··· + X
2
n
的分布称为自由度为 n 的 χ
2
分布,记为 χ
2
∼ χ
2
(n)。其密度函数为:
p(y) =
(
1
2
n/2
Γ(n/2)
y
n
2
−1
e
−
y
2
, y > 0
0 , y ≤ 0
特别地,X ∼ N(µ, σ
2
) ⇒ (
x−µ
σ
)
2
∼ χ
2
(1)
图 3: χ
2
分布密度图像
51
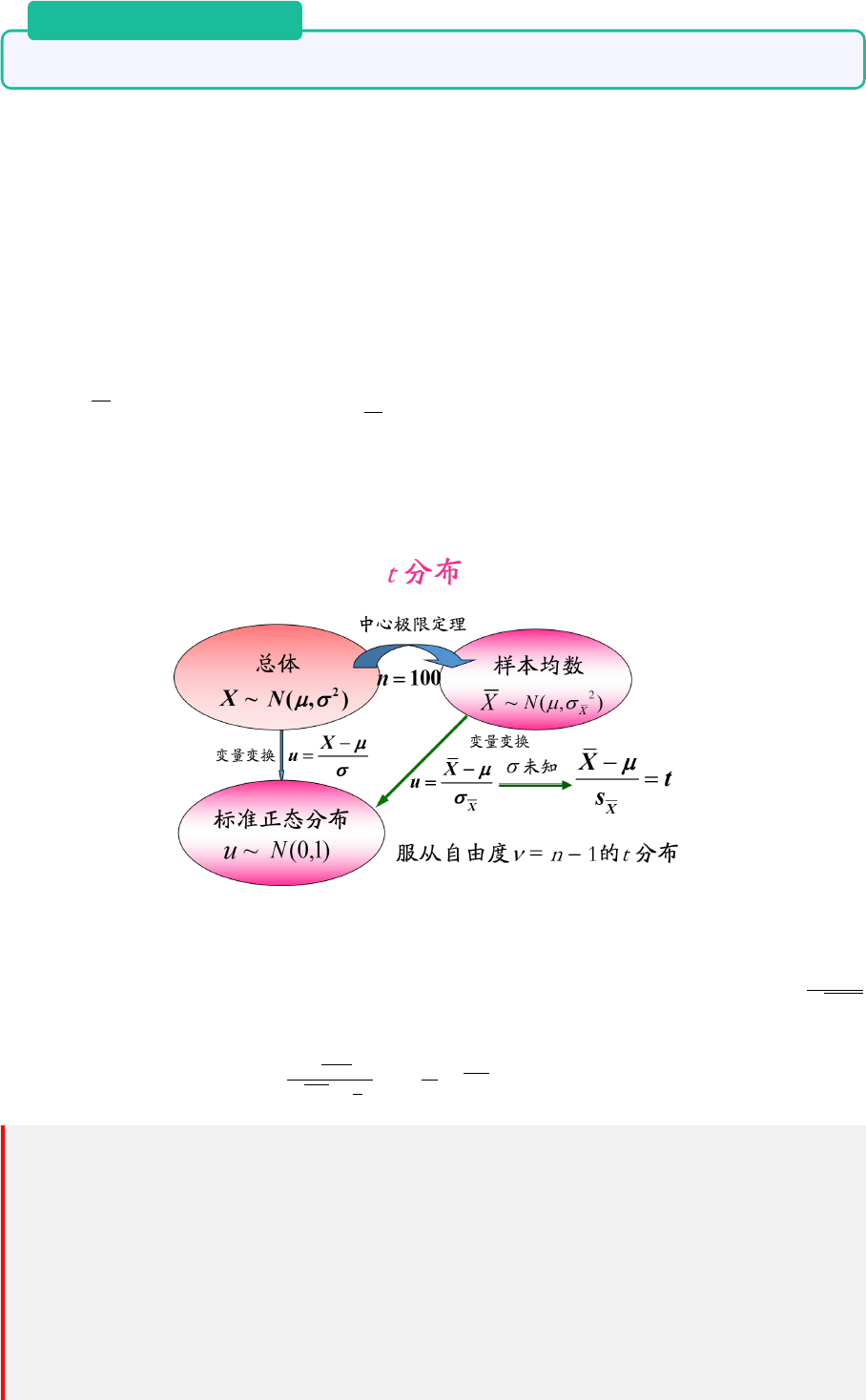
19 抽样分布
该密度函数的图像是一个取非负值的偏态分布,且 Eχ
2
= n, V ar(χ
2
) = 2n。
定理 19.2. χ
2
分布可加性
若 X ∼ χ
2
(n
1
),Y ∼ χ
2
(n
2
),并且 X、Y 独立,则 X + Y ∼ χ
2
(n
1
+ n
2
)。
定义19.7 卡方分布的 1 − α 分位数:当随机变量 χ
2
∼ χ
2
(n) 时,对给定 α(0 < α < 1),称满足
P (χ
2
≤ χ
2
1−α
(n)) = 1 − α 的 χ
2
1−α
(n) 是自由度为 n 的卡方分布的 1 − α 分位数。
19.3.2 t 分布
我们知道正态分布有两个参数:µ 和 σ,决定了正态分布的位置和形态。为了应用方便,常将一
般的正态变量 X 通过 u 变换转化成标准正态变量 u,使得原来各种形态的正态分布都转换为
µ = 0,σ = 1 的标准正态分(standard normal distribution),亦称 u 分布。
根据中心极限定理,若从正态总体 N(µ, σ
2
) 中,反复多次随机抽取样本含量固定为 n 的样本,
样本均数 X 仍服从正态分布,即 N(µ,
σ
2
n
) 。所以,对样本均值的分布进行 u 变换,也可变换
为标准正态分布 N(0, 1)。
在实际工作中,往往 σ 是未知的,常将样本的方差 S
n
作为 σ 的估计值,为了与 u 变换区别,称
为 t 变换,统计量 t 值的分布称为 t 分布。
图 4: t 变换
定义19.8 t 分布:设随机变量 X
1
与 X
2
独立,且 X
1
∼ N(0, 1),X
2
∼ χ
2
(n),则称 t =
X
1
√
X
2
/n
的分布为自由度为 n 的 t 分布,记为 t ∼ t(n)。其概率密度函数为:
p(t) =
Γ(
n+1
2
)
√
nπΓ(
n
2
)
(1 +
t
2
n
)
−
n+1
2
, −∞ < t < ∞
Note: t 分布只有一个参数 ν(自由度),曲线形状与样本含量有关。
当自由度逼近 ∞,t 分布则逼近 u 分布,故标准正态分布是 t 分布的特例,当自由度较大
(如 n ≥ 30) 时,t 分布可用正态分布 N(0, 1) 近似。
重要性质:t
α
(n) = −t
1−α
(n)
▷ 自由度为 1 的 t 分布就是标准柯西分布,它的均值不存在
▷ n > 1 时,t 分布的数学期望存在且为 0
▷ n > 2 时,t 分布的方差存在,且为 n/(n − 2)
52
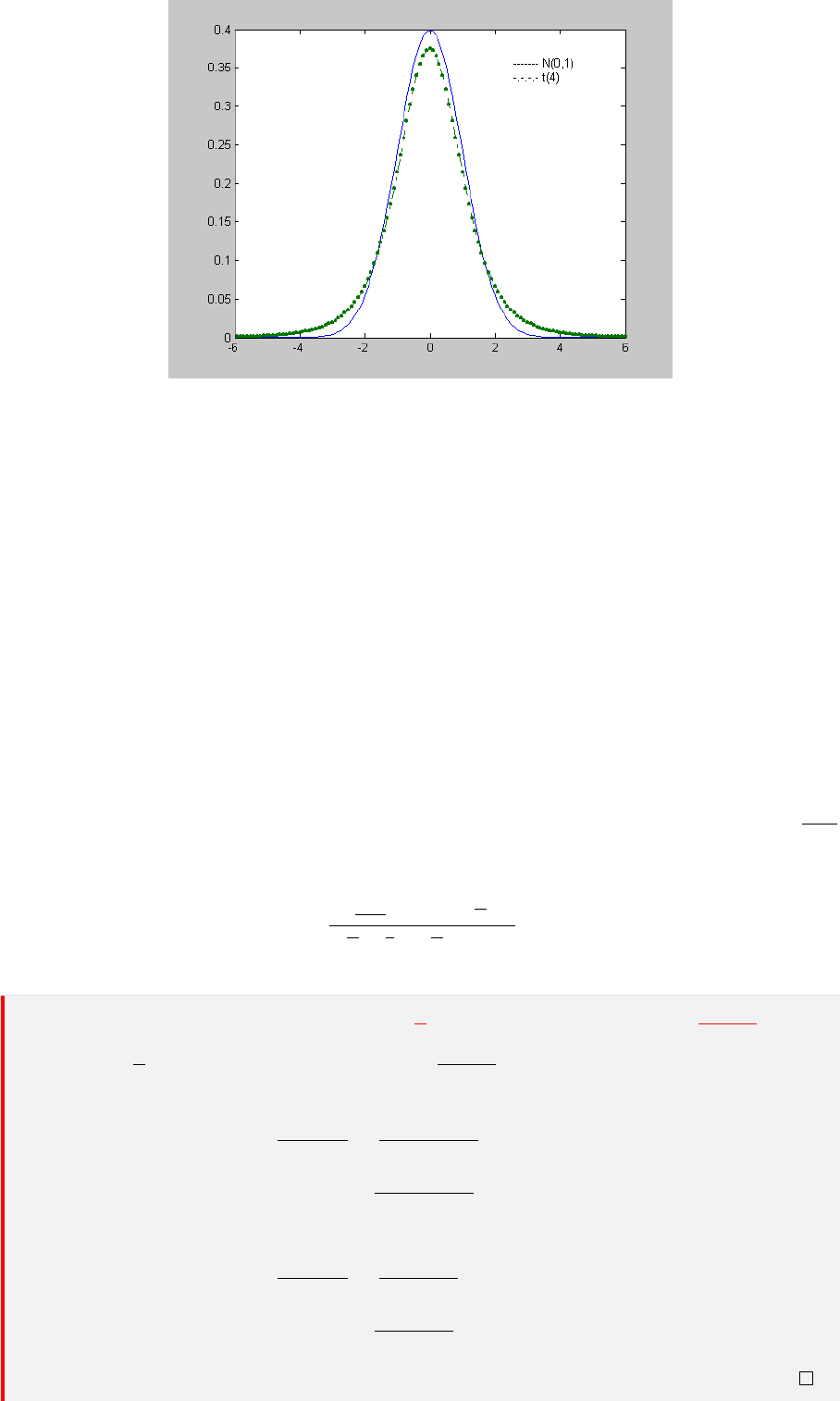
19 抽样分布
图 5: t 分布密度图像
t 分布的密度函数图像是一个关于纵轴对称的分布,与标准正态分布类似,只是峰比标准正态分
布低一些,尾部的概率比标准正态分布的大一些。
定义19.9 t 分布的 1 − α 分位数:当随机变量 t ∼ t(n) 时,称满足 P (t ≤ t
1−α
(n)) = 1 − α 的
t
1−α
(n) 是自由度为 n 的 t 分布的 1 − α 分位数。
使用 t 分布可以在总体标准差未知的情况下分析近似正态总体的均值。例如,t 分布的一个用途
就是检验总体均值与假设均值是否不同。回归系数的显著性检验也使用 t 分布。
19.3.3 F 分布
F 分布是费希尔首先提出的。
定义19.10 t 分布:设 X ∼ χ
2
(m), Y ∼ χ
2
(n),且 X 与 Y 相互独立,则称随机变量 F =
X/m
Y /n
的分布为服从第一自由度 m(分子 X 的自由度)和第二自由度 n(分母 Y 的自由度)的 F 分
布,记做: F ∼ F (m, n)。其概率密度函数为:
h(y) =
Γ(
m+n
2
)(m/n)
m/2
y
m
2
−1
Γ(
m
2
)Γ(
n
2
)(1+
m
n
y)
(m+n)/2
, y > 0
0 , y ≤ 0
Note: 重要性质:如果 F ∼ F (m, n),则
1
F
∼ F (n, m),且 F
1−a
(m, n) =
1
F
a
(n,m)
证明. 已知
1
F
∼ F (n, m),证明 F
1−a
(m, n) =
1
F
a
(n,m)
成立。
P {F (m, n) ≤ F
1−α
(m, n)} = 1 − α ⇔
P {
1
F (m, n)
≥
1
F
1−α
(m, n)
} = 1 − α ⇔
P {F (n, m) <
1
F
1−α
(m, n)
} = α
P {F (n, m) ≤ F
α
(n, m)} = α
P {
1
F (n, m)
>
1
F
α
(n, m)
} = α
P {F (m, n) ≤
1
F
α
(n, m)
} = 1 − α
53
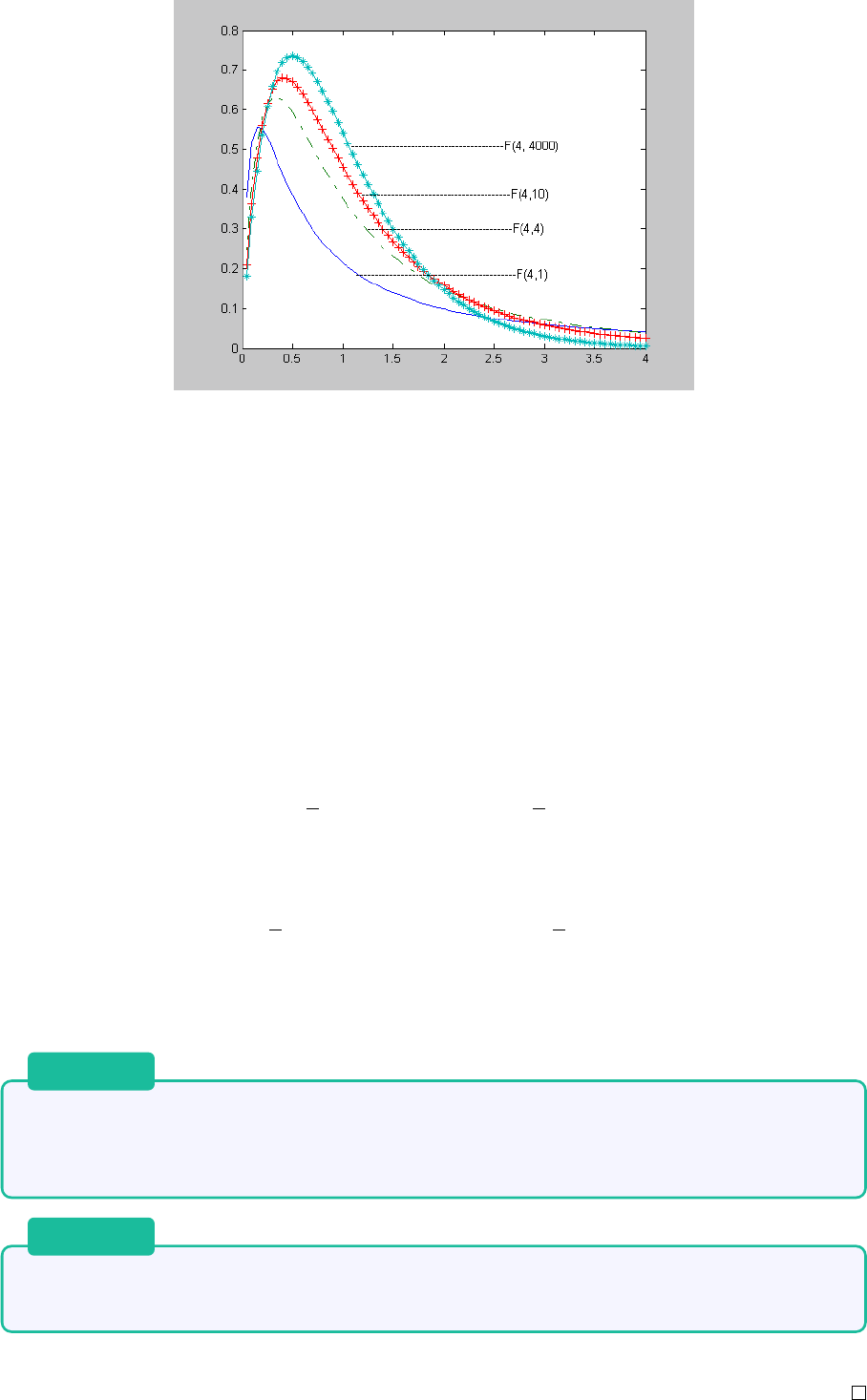
19 抽样分布
图 6: F 分布密度图像
该密度函数的图象也是取非负值的偏态分布。
定义19.11 F 分布的 1 − α 分位数:当随机变量 F ∼ F (m, n) 时,对给定 α(0 < α < 1),称满
足 P (F ≤ F
1−α
(m, n)) = 1 − α 的 F
1−α
(m, n) 是自由度为 m 与 n 的 F 分布的 1 − α 分位数。
19.4 样本均值
定义19.12 :设 x
1
, x
2
, …, x
n
为取自某总体的样本,其算术平均值称为样本均值,一般用 ¯x 表示,
即
¯x =
1
n
(x
1
+ x
2
+ . . . + x
n
) =
1
n
n
X
i=1
x
i
在分组样本场合,样本均值的近似公式为
¯x =
1
n
(x
1
f
1
+ x
2
f
2
+ . . . + x
k
f
k
) =
1
n
k
X
i=1
x
i
f
i
其中 n =
k
P
i=1
f
i
,k 为组数,x
i
为第 i 组的组中值,f
i
为第 i 组的频数。
定理 19.3
若把样本中的数据与样本均值之差称为偏差,则样本所有偏差之和为 0,即
n
X
i=1
(x
i
− x) = 0
定理 19.4
数据观测值与均值的偏差平方和最小,即在形如
P
(x
i
− c)
2
的函数中,
P
x
i
− x
2
最
小,其中 c 为任意给定常数。
证明.
54
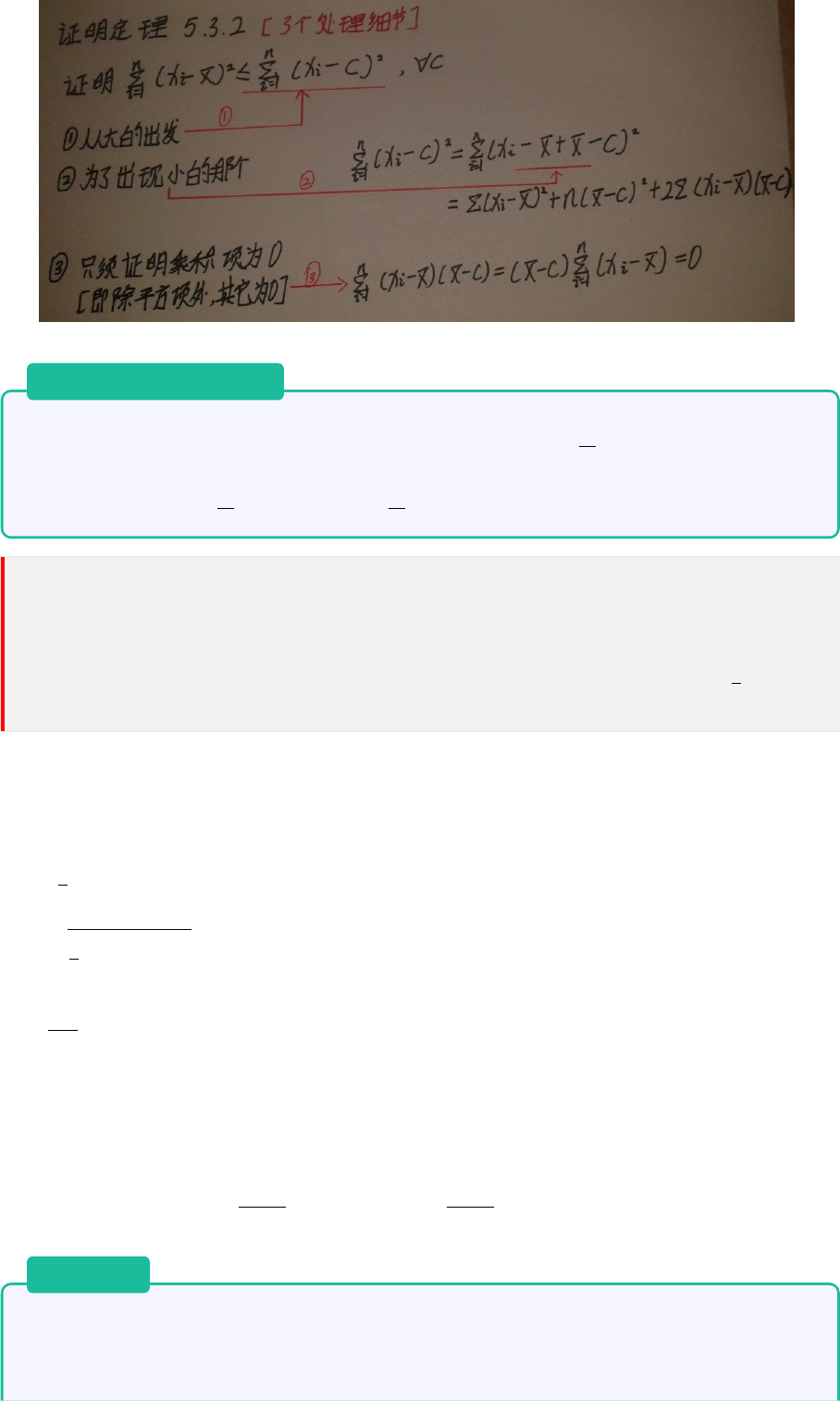
19 抽样分布
定理 19.5.
¯
x 的抽样分布
设 x
1
, x
2
, . . . , x
n
是来自总体 X 的样本,x 为样本均值。
1. 若总体 X 的分布为 N (µ, σ
2
),则 x 的精确分布为 N(µ,
σ
2
n
)
2. 若总体分布未知或不是正态分布,但 E(x) = µ,Var(x) = σ
2
,则 n 较大时 x 的渐
近分布为 N(µ,
σ
2
n
),常记 x ˙∼N(µ,
σ
2
n
)。这里渐近分布是指 n 较大时的近似分布。
Note: 从定理19.5可以看出:
1. 不论总体服从什么分布,样本均值永远服从正态分布。若总体未知,则样本均值近似
正态,若总体正态,则样本均值精确正态。
2. 样本均值的期望永远等于总体的期望,样本均值的方差,永远等于总体的
1
n
。(参考
定理19.6)
19.5 样本方差与样本标准差
s∗
2
=
1
n
n
P
i=1
(x
i
− ¯x)
2
——未修正的样本均值平均偏差平方和,即样本方差。
s∗ =
s
1
n
n
P
i=1
(x
i
− ¯x)
2
——未修正的样本标准差。
s
2
=
1
n−1
n
P
i=1
(x
i
− ¯x)
2
——n 不大时,修正的样本方差,即无偏方差。
n
P
i=1
(x
i
− ¯x)
2
=
n
P
i=1
x
2
i
− n¯x
2
=
n
P
i=1
(x
2
i
− ¯x
2
) ——样本偏差平方和。
分组样本的样本方差近似公式
s
2
=
1
n − 1
k
X
i=1
f
i
(x
i
− ¯x)
2
=
1
n − 1
"
k
X
i=1
f
i
x
2
i
− n¯x
2
#
定理 19.6
a
设总体 X 具有二阶矩,即 E(x) = µ,Var (x) = σ
2
< ∞,x
1
, x
2
, . . . , x
n
为从该总体得
到的样本,x 和 s
2
分别是样本的均值与方差,则:
E(X) = µ
55
19 抽样分布
Var(X) =
σ
2
n
E(S
2
) = σ
2
a
该定理可能出自 Gauss。
Note: 定理19.6揭示了样本均值的数学期望和方差,以及样本方差的数学期望都不依赖
于总体的分布形式。
定理19.6可结合定理19.5来理解。
19.6 一些重要的结论
定理 19.7
设 x
1
, x
2
, . . . , x
n
是来自 N (µ, σ
2
) 的样本,其样本均值和样本方差分别为 ¯x =
1
n
n
P
i=1
x
i
和
s
2
=
1
n−1
n
P
i=1
(x
i
− ¯x)
2
则有:
1. ¯x 与 s
2
相互独立
Note: 只是正态总体下的样本方差和样本均值相互独立。
证明参见:正态分布总体样本均值与方差独立性证明
2. ¯x ∼ N (µ,
σ
2
n
) 或者
¯x−µ
σ/
√
n
∼ N(0, 1)
3.
(n−1)s
2
σ
2
∼ χ
2
(n − 1) 或者
n
P
i=1
(
x
i
−¯x
σ
)
2
∼ χ
2
(n − 1)
Note: 这里要注意,虽然
x−µ
σ
∼ N(0, 1),但是没有
x−¯x
σ
∼ N(0, 1),所以这
并不能根据卡方分布的定义得出。
4.
n
P
i=1
(
x
i
−µ
σ
)
2
∼ χ
2
(n)
5.
¯x−µ
s/
√
n
∼ t(n − 1)
Note:
证明.
¯x−µ
σ/
√
n
∼ N(0, 1),
(n−1)s
2
σ
2
∼ x
2
(n − 1)
因为 ¯x 与 s
2
相互独立,所以二者相互独立(µ 和 σ 可看作常数),由 t 分布
的定义可知
¯x −µ
σ/
√
n
/
r
(n − 1)s
2
/σ
2
n − 1
=
√
n(¯x − µ)
s
∼ t(n − 1)
定理 19.8
设 x
1
, x
2
, . . . , x
m
是来自 N(µ
1
, σ
2
1
) 的样本,y
1
, y
2
, . . . , y
n
是来自 N(µ
2
, σ
2
2
) 的样本,且此
两样本相互独立,则有:
56

20 参数估计
Note: s
2
x
=
1
m−1
m
P
i=1
(x
i
− ¯x)
2
、s
2
y
=
1
n−1
n
P
i=1
(y
i
− ¯y)
2
、¯x =
1
m
m
P
i=1
x
i
、¯y =
1
n
n
P
i=1
y
i
1.
(¯x−¯y)−(µ
1
−µ
2
)
σ
2
1
m
+
σ
2
2
n
∼ N(0, 1)
Note:
x ∼ N(µ
1
,
σ
2
1
m
), y ∼ N (µ
2
,
σ
2
2
n
)
D
X −Y
= DX + D Y
x − y ∼ N (µ
1
− µ
2
,
σ
2
1
m
+
σ
2
2
n
)
2.
(m−1)s
2
1
σ
2
1
+
(n−1)s
2
2
σ
2
2
∼ χ
2
(m + n − 2),另外
m
P
i=1
(
x
i
−u
1
σ
1
)
2
+
n
P
i=1
(
y
i
−u
2
σ
2
)
2
∼ χ
2
(m + n)
Note:
m
P
i=1
(
x
i
−¯x
σ
1
)
2
+
n
P
i=1
(
y
i
−¯y
σ
2
)
2
∼ χ
2
(m + n − 2),卡方分布的可加性
3. F =
s
2
1
/σ
2
1
s
2
2
/σ
2
2
∼ F (m −1, n −1),特别地,若 σ
2
1
= σ
2
2
,则 F = s
2
1
/s
2
2
∼ F (m −1, n −1)
Note:
(m−1)s
2
x
σ
2
1
∼ χ
2
(m − 1)、
(n−1)s
2
x
σ
2
2
∼ χ
2
(n − 1),根据 F 分布的定义
4. 若 σ
2
1
= σ
2
2
= σ
2
,则
(¯x−¯y)−(µ
1
−µ
2
)
s
w
1
m
+
1
n
∼ t(m + n − 2),其中 s
w
=
q
(m−1)s
2
1
+(n−1)s
2
2
m+n−2
Note: 已知
(¯x−¯y)−(µ
1
−µ
2
)
σ
2
m
+
σ
2
n
∼ N(0, 1) 和
(m−1)s
2
x
σ
2
1
∼ χ
2
(m − 1)、
(n−1)s
2
x
σ
2
2
∼
χ
2
(n − 1)
由卡方分布的可加性:
(m + n − 2)s
2
w
σ
2
=
(m − 1)s
2
x
+ (n − 1)s
2
y
σ
2
∼ χ
2
(m + n − 2)
20 参数估计
20.1 矩估计
替换原理
1. 用样本矩去代替对应的总体矩
2. 用样本矩的函数代替对应的总体矩的函数
Note: 当总体 k 阶矩存在时,样本 k 阶原点矩是总体 k 阶原点矩的无偏估计。所以,
对任一总体而言,样本均值是总体均值的无偏估计。但对 k 阶中心矩则不一样,例如样本
方差就不是总体方差的无偏估计。
但当 n → ∞ 时,样本 k 阶中心矩可看作总体 k 阶中心矩的无偏估计。
57
20 参数估计
矩估计的方法 设总体的概率函数为 p(x; θ
1
, . . . , θ
k
),x
1
, x
2
, . . . , x
n
是样本,假定总体的 k 阶原
点矩 u
k
存在,从而 u
j
= u
j
(θ
1
, . . . , θ
k
),则有方程组
ˆµ
1
= a
1
ˆµ
2
= a
2
ˆµ
k
= a
k
即
µ
1
(
ˆ
θ
1
,
ˆ
θ
2
, ···
ˆ
θ
k
) = a
1
µ
2
(
ˆ
θ
1
,
ˆ
θ
2
, ···
ˆ
θ
k
) = a
2
µ
k
(
ˆ
θ
1
,
ˆ
θ
2
, ···
ˆ
θ
k
) = a
k
⇒
ˆ
θ
1
=
ˆ
θ
1
(a
1
, a
2
, ··· , a
k
)
ˆ
θ
2
=
ˆ
θ
2
(a
1
, a
2
, ··· , a
k
)
ˆ
θ
k
=
ˆ
θ
k
(a
1
, a
2
, ··· , a
k
)
其中,a
k
=
1
n
n
P
i=1
x
k
i
由上述方程组求出来的 (
ˆ
θ
1
,
ˆ
θ
2
, ··· ,
ˆ
θ
k
) 就称之为未知参数向量 (θ
1
, θ
2
, ··· , θ
k
) 的矩估计(量)。
20.1.1 缺陷
矩估计的优点是计算简单, 但是它也有一些缺点:
1. 不同的做法会得到不同的解,也就是矩估计可能是不唯一的,此时通常应该尽量采用低阶
矩给出未知参数的估计。
2. 得到不合理的解。
如总体 X 服从 [0, θ] 的均匀分布,由矩估计法可知 θ 的矩估计量为
ˆ
θ = 2
¯
X,样本
(X
1
, X
2
, ··· , X
5
) = (1, 2, 3, 5, 9),样本矩为 4,故
ˆ
θ = 2
¯
X = 8 。也就是说总体 X ∼ U (0, 8)。
但 X
5
= 9,该值大于 8,所以
ˆ
θ = 8 的估计是不合理的。
3. 总体分布的矩不一定存在,所以矩估计法不一定有解。
20.2 极 (最) 大似然估计
极大似然原理
事件 A 与参数 θ ∈ Θ 有关,θ 取值不同,则 P (A) 也不同,若 A 发生了,则认为此时的
θ 值就是 Θ 的估计值。
定义20.1 似然函数:设总体的概率函数为 P (x; θ),Θ 是参数 θ 可能取值的参数空间,x
1
, x
2
, . . . , x
n
是样本,将样本的联合概率函数看成 θ 的函数,用 L(θ; x
1
, x
2
, . . . , x
n
) 表示,简记为 L(θ),称
为样本的似然函数。
Note: 似然函数就是联合概率密度函数,并且一定是指样本的似然函数。
特别地,如果 X
1
, ··· , X
n
独立同分布,则 L(θ) = L(θ; x
1
, ··· , x
n
) = p(x
1
; θ) · p(x
2
; θ) ·
··· · p(x
n
; θ)。
定义20.2 极大似然估计:x
1
, ··· , x
n
是 X
1
, ··· , X
n
的一组观察值,如果某统计量
ˆ
θ =
ˆ
θ(x
1
, ··· , x
n
)
满足 L(
ˆ
θ) = max
θ∈Θ
L(θ),则称
ˆ
θ 是 θ 的极 (最) 大似然估计,简记为 MLE(Maximum Likelihood
Estimate)。
Note: 因为 ln x 是 x 的单调递增函数,所以对 ln L(θ) 求最大值解出的 θ 和对 L(θ) 求
最大值接触的 θ 是等价的,但人们更习惯于用 ln L(θ) 求极大似然估计。当 L(θ) 是可微函
数时,求导是求极大似然估计值的常用方法,而对数函数求导比较简单。
极大似然估计并不局限于独立同分布的样本,只要样本的联合密度已知,就可以用 MLE
的方法来估计未知参数。
极大似然估计是基于具体的样本的,但作推导的时候不需要先代入样本值,只需要将样本
58

20 参数估计
值代入推导结果。
求极大似然估计的步骤 设 X
1
, ··· , X
n
iid
∼ p(x; θ),θ = (θ
1
, θ
2
, ··· , θ
k
) ∈ Θ,求 θ 的极大似然估
计:
1. 求似然函数:L(θ) = L(x
1
, ··· , x
n
; θ) =
n
Q
i=1
p(x
i
; θ)
2. 求解似然方程 (组)(即求极值点 (最值点))
∂L
∂θ
1
= 0
∂L
∂θ
2
= 0
···
∂L
∂θ
k
= 0
3. 为了简化,取似然函数的对数:ln L(θ) = L(x
1
, ··· , x
n
; θ) =
n
P
i=1
ln p(x
i
; θ)
4. 求解对数似然方程
(
组
)
,即得到
θ
的极大似然估计
∂ ln L
∂θ
1
= 0
∂ ln L
∂θ
2
= 0
···
∂ ln L
∂θ
k
= 0
极大似然估计的不变性
如果
ˆ
θ 是 θ 的极大似然估计,则对任一函数 g(θ),其极大似然估计为 g(
ˆ
θ)。
20.3 点估计
定义20.3 点估计:设 x
1
, x
2
, ··· , x
n
来自总体 X 的一个样本,我们用一个统计量
ˆ
θ =
ˆ
θ(x
1
, ··· , x
n
)
的取值作为 θ 的估计值,称为为 θ 的点估计(量),简称估计。
Note: 在这里如何构造统计量并没有明确的规定,只要它满足一定的合理性即可。
这就涉及到两个问题:
1. 如何给出估计,即估计的方法问题;
2. 如何对不同的估计进行评价,即估计的好坏判断标准。
20.4 区间估计
定义20.4 双侧置信区间:设 θ 是总体的一个参数,其参数空间为 Θ,x
1
, x
2
, ··· , x
n
是来自该总
体的样本,对给定的一个 α(0 < α < 1),若有两个统计量
ˆ
θ
L
=
ˆ
θ
L
(x
1
, x
2
, ··· , x
n
) 和
ˆ
θ
U
=
ˆ
θ
U
(x
1
, x
2
, ··· , x
n
),对任意 θ ∈ Θ,有
P
n
ˆ
θ
L
≤ θ ≤
ˆ
θ
U
o
≥ 1 − α
则称随机区间 [
ˆ
θ
L
,
ˆ
θ
U
] 为参数 θ 的置信度为 1 − α 的置信区间,
ˆ
θ
L
和
ˆ
θ
U
分别称为(双侧)置
信下限和上限。置信度 1 − α 也称置信水平。
Note: 置信区间是以统计量为端点的随机区间。
定义20.5 同等置信区间:沿用定义20.4的记号,如果对给定的 α 0 < α < 1,对任意的,有
59
20 参数估计
P
n
ˆ
θ
L
≤ θ ≤
ˆ
θ
U
o
= 1 − α
则称 [
ˆ
θ
L
,
ˆ
θ
U
] 为 θ 的 1 − α 同等置信区间。
定义20.6 :设
ˆ
θ
L
=
ˆ
θ
L
(x
1
, x
2
, ··· , x
n
) 是统计量,对给定的 α(0 < α < 1),对任意的 θ ∈ Θ,有
P
n
ˆ
θ
L
≤ θ
o
≥ 1 − α 则称
ˆ
θ
L
为 θ 的置信水平为 1 − α 的 (单侧) 置信下限。假如等号对一切
θ ∈ Θ 成立,则称
ˆ
θ
L
为 θ 的 1 − α 同等置信下限。
设
ˆ
θ
U
=
ˆ
θ
U
(x
1
, x
2
, ··· , x
n
) 是统计量,对给定的 α(0 < α < 1),对任意的 θ ∈ Θ,有 P
n
θ ≤
ˆ
θ
U
o
≥
1 − α 则称
ˆ
θ
U
为 θ 的置信水平为 1 − α 的 (单侧) 置信上限。假如等号对一切 θ ∈ Θ 成立,则
称
ˆ
θ
U
为 θ 的 1 − α 同等置信上限。
20.4.1 构造置信区间——枢轴量法
构造未知参数 θ 的置信区间的最常用的方法是枢轴量法,其步骤可以概括为如下三步:
1. 设法构造一个样本和 θ 的函数 G = G(θ; x
1
, x
1
, ··· , x
n
) 使得 G 的分布不依赖于未知参数。
称具有这种性质的 G 为枢轴量。
2. 适当地选择两个常数 c, d,使对给定的 α(0 < α < 1) 有 P (c ≤ G ≤ d) = 1 − α。
3. 将 c ≤ G ≤ d 等价变形为
ˆ
θ
1
≤ θ ≤
ˆ
θ
2
,则 (
ˆ
θ
1
,
ˆ
θ
2
) 是 θ 的 1 − α 同等置信区间。
Note: 枢轴量法中构造枢轴量 G 的三个关键点:
1. G 要与所讨论的未知参数相关
2. G 与其他未知参数无关
3. G 的分布与未知参数无关(G 的分布已知)
20.4.2 构造置信区间的原则
区间最短原则 满足置信度要求的 c 与 d 通常不唯一。对同一置信度,区间平均长度越短越好;
若有可能,应选平均长度达到最短的 c 与 d。但实际中,选平均长度尽可能短的 c 与 d,这往往
很难实现。
对称原则
取对称区间
几何对称
G 的分布为对称分布
概率对称
G 的分布为偏态分布
所谓概率对称指的是选择这样的 c 与 d,使得两个尾部概率各为 α/2,即 P (G < c) = P (G >
d) = α/2,这样得到的置信区间称为等尾置信区间,实际中,实用的置信区间都是等尾置信区间。
60

20 参数估计
Note: 总之一个总的原则是:在保证一定的置信度的条件下,优先考虑区间最短原则,其
次考虑几何对称原则和概率对称原则。
20.4.3 区间估计与点估计的联系
本质上,区间估计就是两个点估计(点估计的方法可不局限于矩估计、极大似然估计)。也就是
估计 θ
L
, θ
U
。虽然,矩估计、极大似然估计都是估计出一个点,但是它们并非只用于点估计,也
会用于区间估计。举个例子,当对总体矩 θ 的区间进行估计时,所选用的枢轴量 G 一般和
ˆ
θ、θ
两者相关。
20.5 点估计量的评判标准
点估计其实就是样本的统计量,统计量是一个随机变量,它不可能完全等于真值。那么我们如何
判断一个点估计的好坏呢?
20.5.1 相合性
思想:既然不能要求点估计等于真值,但根据格里纹科定理,要求点估计随着样本量的不断增大
的时候逼近参数真值并不过分。
ˆ
θ 是 θ 的一个估计,虽然不能要求
ˆ
θ = θ,但可要求
ˆ
θ 在 θ 的附近波动,并随着样本量的增多,
波动幅度越小。
定义20.7 相合性:设 θ ∈ Θ 为未知参数,
ˆ
θ
n
=
ˆ
θ
n
(x
1
, ··· , x
n
) 是 θ 的一个估计量,若对任何一
个 ε > 0,有 lim
n→∞
P (|
b
θ
n
−θ| > ε) = 0(或 lim
n→∞
P (|
b
θ
n
−θ| ≤ ε) = 1)则称为 θ 参数的相合估计
(量)。
Note: 相合性就是指
ˆ
θ
n
依概率收敛于 �。
由此可见,相合估计量仅在样本容量 n 足够大时,才显示其优越性。相合性在别的地方可能被
称为一致性。
关于相合性的两个常用结论:
1. 样本 k 阶矩是总体 k 阶矩的相合估计:由大数定律可证明。即:矩估计是相合估计量。
由此可推论得:矩估计即相合估计。那么只需证明
ˆ
θ 是 θ 的矩估计,即可证明
ˆ
θ 是 θ 的相
合估计。
2. 设
ˆ
θ 是 θ 的无偏估计量,则 lim
n→∞
V ar(
ˆ
θ) = 0,则
ˆ
θ 是 � 的相合估计:用切贝雪夫不等式
可证明。
定理 20.1
设
ˆ
θ
n
=
ˆ
θ
n
(x
1
, ··· , x
n
) 是 θ 的一个估计量,若 E(
ˆ
θ
n
) = θ ,Var(
ˆ
θ
n
) = 0,则
ˆ
θ 是 θ 的相
合估计。
定理 20.2
若
ˆ
θ
n1
, ··· ,
ˆ
θ
nk
分别是 θ
1
, …, θ
k
的相合估计,η = g(θ
1
, …, θ
k
) 是 θ
1
, …, θ
k
的连续函数,则
ˆη
n
= g(
ˆ
θ
n1
, ··· ,
ˆ
θ
nk
) 是 η 的相合估计。
61

20 参数估计
书本 310-311 页
20.5.2 无偏性
思想:既然不能要求点估计等于真值,但要求进行多次抽样,多个样本的点估计的期望等于真值
并不过分。
定义20.8 无偏性:设
ˆ
θ =
ˆ
θ
n
(x
1
, ··· , x
n
) 是 θ 的一个估计,θ 的参数空间为 Θ,若对任意的 θ ∈ Θ,
有 E
ˆ
θ
n
= θ,则称
ˆ
θ 是 θ 的无偏估计,否则称为有偏估计。
Note: 无偏估计不具有不变性,即若
ˆ
θ 是 θ 的无偏估计,一般而言,其函数 g(
ˆ
θ) 不是
g(θ) 的无偏估计,除非 g(θ) 是 θ 的线性函数。例如 s
2
=
1
n−1
P
i=1
n
(x
i
− ¯x) 是 σ
2
的无偏
估计,但 s 不是 σ 的偏估计。
20.5.3 有效性
思想:既然不能要求点估计等于真值,但要求点估计偏离真值的程度较小并不过分。
注意的是,这里有效性要分为两种情况——无偏估计和有偏估计。
定义20.9 一致最小方差无偏估计:设
ˆ
θ
1
,
ˆ
θ
2
是 θ 的两个无偏估计,如果对任意的 θ ∈ Θ,有
V ar(
ˆ
θ
1
) ≤ V ar(
ˆ
θ
2
),且至少有一个 θ ∈ Θ 使得上述不等号严格成立。则称
ˆ
θ
1
比
ˆ
θ
2
有效,
ˆ
θ 是
θ 的一致最小方差无偏估计,简记为 UMVUE。
很显然,因为
ˆ
θ
1
,
ˆ
θ
2
是 θ 的无偏估计,所以有 E(
ˆ
θ
1
) = E(
ˆ
θ
0
) = θ,因此 V ar(
ˆ
θ
1
) = E(
ˆ
θ
1
−E(
ˆ
θ
1
))
2
=
E
(
ˆ
θ
1
−
θ
)
2
定义20.10 一致最小均方误差估计:设
ˆ
θ
1
,
ˆ
θ
2
是 θ 的两个无偏估计,MSE(
ˆ
θ) = E(
ˆ
θ − θ)
2
。我们
希望估计的均方误差越小越好。
因为
ˆ
θ 是 θ 的两个无偏估计,所以 E(
ˆ
θ) ̸= θ。
注意到 MSE
ˆ
θ
= Var
ˆ
θ
+
E
ˆ
θ − θ
2
,因此均方误差由两部分组成,点估计的方差与偏差的
平方。如果点估计是无偏的,则均方误差等于其方差。
MSE(
ˆ
θ) = E(
ˆ
θ − θ)
2
= [E(
ˆ
θ − E
ˆ
θ) + (E
ˆ
θ − θ)]
2
= E(
ˆ
θ − E
ˆ
θ)
2
+ (E
ˆ
θ − θ)
2
+ 2E[(
ˆ
θ − E
ˆ
θ)(E
ˆ
θ − θ)]
= V ar(
ˆ
θ) + (E
ˆ
θ − θ)
2
20.5.4 直观理解各标准的区别
图7:红色线是有偏的,但是符合相合性;蓝色线是无偏的,但是不符合相合性。而从上图可以
看出,当样本量达到一定程度,无偏估计量不一定优于相合估计量。
图8:1、2 是无偏的,但 2 更有效;3、4 是有偏的,但 4 更有效。
图9:如图所示,无偏估计量不一定优于有偏估计量。说到底,精度才是决定估计量优劣的根本。
62
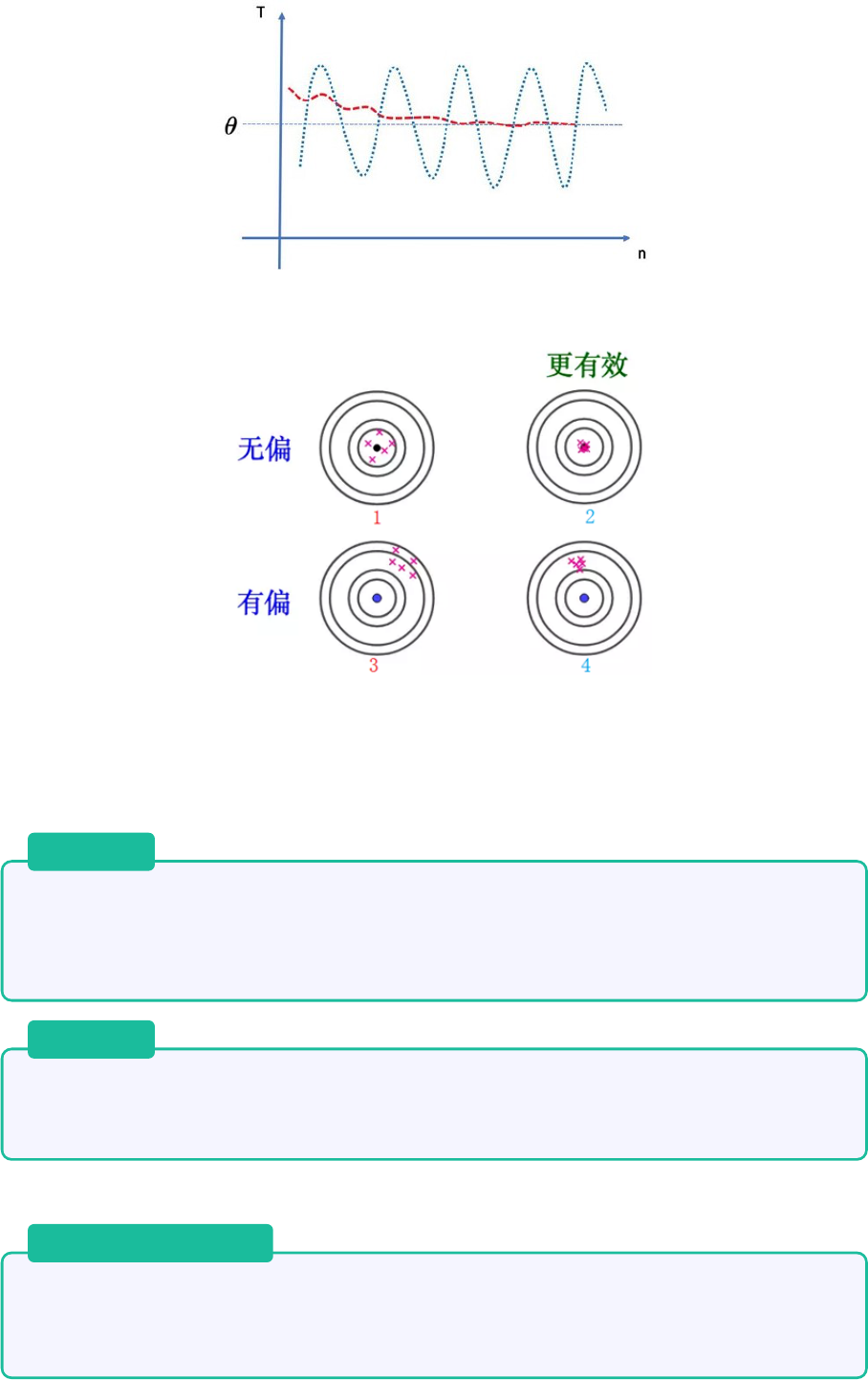
20 参数估计
图 7: 相合性与无偏性
图 8: 无偏性与有效性
20.6 判断 UMVUE
定理 20.3
设 x = (x
1
, x
2
, …, x
n
) 是来自某总体的一个样本,
ˆ
θ =
ˆ
θ(X) 是 θ 的一个无偏估计,Var(
ˆ
θ) <
∞。则
ˆ
θ 是 θ 的 UMVUE 的充要条件是,对任意一个满足 E(φ(X)) = 0 和 Var(φ(X)) <
∞ 的 (X),都有
Cov
θ
(
ˆ
θ, φ) = 0, ∀θ ∈ Θ
定理 20.4
设 X、Y 是两个随机变量,EX = µ,VarX > 0,记 φ(Y ) = E(X|Y ),则有
E(φ(Y )) = µ, V ar(φ(Y )) ≤ V ar(X)
其中等号成立的充要条件是 X 和 φ(Y ) 几乎处处相等。
从定理20.4直接得到下述定理。
定理 20.5. 充分性原则
设总体概率函数是 p(x, ),x
1
, x
2
, …, x
n
是其样本,T = T (x
1
, x
2
, …, x
n
) 是 θ 的充分统计
量,则对 θ 的任一无偏估计
ˆ
θ =
ˆ
θ
n
(x
1
, ··· , x
n
),令
∼
θ = E(
ˆ
θ|T ),则
∼
θ 也是 θ 的无偏估
计,且 Var(
∼
θ) ≤ Var(
ˆ
θ)。
好的无偏估计都是充分统计量的函数;如果一个无偏估计不是充分统计量的函数,可以将其对充
分统计量求条件期望,便得到一个新的无偏估计。新的无偏估计更有效,更可贵的是还充分。
63

21 假设检验
图 9: 无偏性与有效性
换言之,考虑 θ 的估计问题只需要基于充分统计量的函数进行即可,这便是所谓的充分性原则。
21 假设检验
21.1 小概率原理与统计归谬法
小概率原理
小概率事件在一次试验中是几乎不可能发生的。如果对总体的某个假设是真实的,那么不
利于或不能支持这一假设的小概率事件 A 在一次试验中是几乎不可能发生的;如果在一
次试验中事件 A 竟然发生了,我们就有理由怀疑这一假设的真实性,拒绝这一假设。
实际上,假设检验是数学中反证法的推广。数学反证法, 是将预期要被推翻的说法放在 H
0
, 而
其相反的说法放在 H
1
; 当 H
0
果真被推翻时, 等同于支持了 H
1
的正确性。而何时 H
0
可被被
推翻? 就是当 H
0
衍伸或推论出来的结果为绝不可能发生的事 (如「太阳从西边升起」, 或「0 =
1」) 时, 就果断推论 H
0
绝对错误 (即, H
1
绝对正确)。
在数学反证法中,H
0
或 H
1
是必然事件或不可能事件。而在假设检验中,H
0
或 H
1
往往不是必
然事件或不可能事件,它们往往是有可能发生的事件。也就是说,当 H
0
衍伸或实验出来的结果
为不太可能发生的事 (如「公正铜板连掷 30 次皆反面」) 时, 就推论,H
0
非常可能是错误 (即
H
1
很可能正确)。
在数学反正法中,H
0
是难以证实
6
而易于证伪的;但在假设检验中,H
0
与 H
1
都是不能证实与
证伪的。假设检验与数学反证法的根本区别在于是否基于概率进行判断。
在反证法中,数学家会将需要推翻的命题放在 H
0
,需要证明的命题放在 H
1
。我相信这很容易
理解,因为要证明的命题是难以证实而易于证伪的,如果将需要证明的命题放在 H
0
,那么我们
就选择了一项更难的工作,甚至最后得不到结果。
在这一点上,假设检验与反证法相似,也是将想要推翻的假设放在 H
0
,但原因却和反证法的不
一样。简而言之,是因为假设检验只能控制其中一类错误发生的概率。至于为什么,在讲述 α 错
误的时候会详细说明,这时理解假设检验的关键一点。而另一个关键点是理解 P 值。
Note: 为什么要做假设检验?
两个总体的统计量不相等,不能马上就认为两个总体的参数不相等。产生差异的原因有两
种可能:
1. 样本统计量与相应总体参数的的确存在差异。
2. 两个样本统计量之间的差异,即是“抽样误差”。
6
包括了不能被证实的情况。
64

21 假设检验
因此,我们需要通过假设检验来得出一个结论:是总体存在差异,还是抽样误差的影响。
为什么会有抽样误差? 因为研究的是变量,个体不一定能代表总体。
21.2 相关概念
定义21.1 :假设检验问题就是研究如何根据抽样后获得的样本来检查抽样前对总体所作的假设
是否合理。
定义21.2 势函数: H
0
: θ ∈ Θ
0
vs H
1
: θ ∈ Θ
1
的拒绝域为 W ,则样本观测值 X 落在拒绝域
W 内的概率称为该检验的势函数,记为 g(θ) = P
θ
(X∈ W ),θ ∈ Θ = Θ
0
S
Θ
1
即:
g(θ) =
α(θ), θ ∈ Θ
0
1 − β(θ), θ ∈ Θ
1
定义21.3 统计假设:我们把任一关于总体分布的假设,统称为统计假设,简称假设。
定义21.4 原假设(零假设):一般是需要反对的假设,记作 H
0
。
定义21.5 备择假设:一般是希望证实的假设,记作 H
1
或者 H
a
。
Note: 原假设 H
0
与备择假设 H
1
相互对立,而且两者只有一个正确。
假设检验不能判断对错。
假设检验的三种基本形式:
1. H
1
: θ ̸= θ
0
(双侧检验(假设))
2. H
1
: θ > θ
0
(右侧检验)
3. H
1
: θ < θ
0
(左侧检验)
定义21.6 拒绝域:能够做出拒绝原假设这一结论的所有可能的样本取值范围。
若將估計量的可能數值,劃分為兩個互斥的子集合:其一為 C 集合,通常稱為拒絕域、棄卻域、
危險域(critical region,CR);另一為 C 的餘集合 C�,通常稱為接受域(accept region,AR)。
双侧检验的拒绝域在抽样分布的两一侧;单侧检验的拒绝域在抽样分布的某一侧。
定义21.7 臨界值(critical value):為兩個互斥區域 C 與 C� 的分界點。
图
10:
P
值、临界点、拒绝域示意图
定义21.8 两类错误:
第一类错误:原假设正确,却拒绝了原假设。其发生的概率是 α,即是检验的显著性水平。其它
名字:弃真/拒真错误;α 错误
第二类错误:备择假设正确,却不拒绝原假设。其发生的概率记为 β。其它名字:取伪错误
β = P (Not rejectedH
0
|H
1
)
65
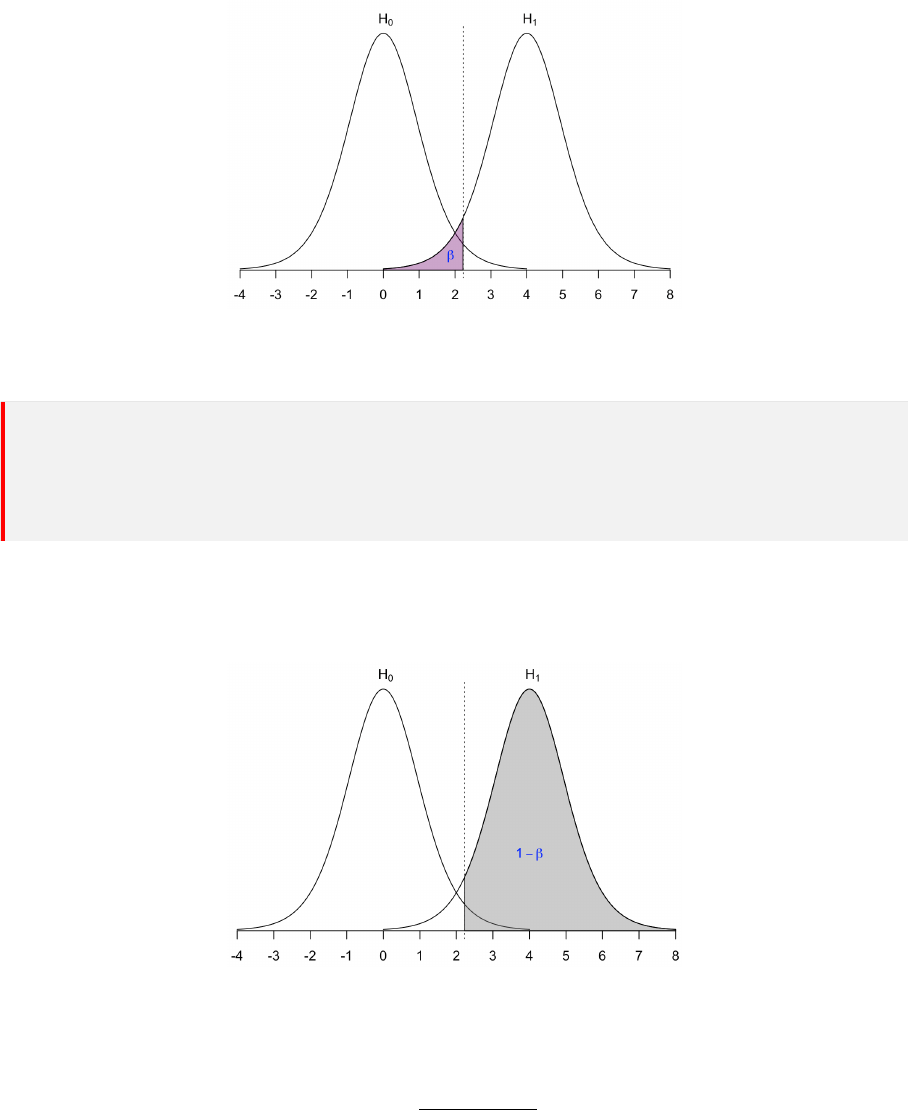
21 假设检验
图 11: β
Note: 错误存在的原因:判断的依据是随机统计量。
其它条件不变,减少第一类错误的概率,便增加第二类错误的概率。
增加样本可同时减少两类错误的概率。
定义21.9 统计效力(statistical power):
1 − β = P (rejected H
0
|H
1
)
图 12: 1 − β
定义21.10 效应值(Eect size): H
0
分布和 H
1
分布的标准化距离。
D =
M
H0
− M
H1
SD
p
SD
p
指 H
0
和 H
1
的合并标准差。
根据图13可知,效应值大小影响了 H
0
分布和 H
1
分布之间的分离程度。效应值越大,同样 P 值
情况下,统计的效力(1 − β)就越大。
如图14在效应值不变的情况下,P 值越大,统计效力(1 − β)就越大。
独立样本 t 检验中,假设两个样本的样本量均为 n = 10,标准差均为 σ
2
= 1,效应值为 D = 1.32,
那么统计效力和 P 值的关系如图15。
21.3 α 错误
假设检验中有两类错误,如下表:
66
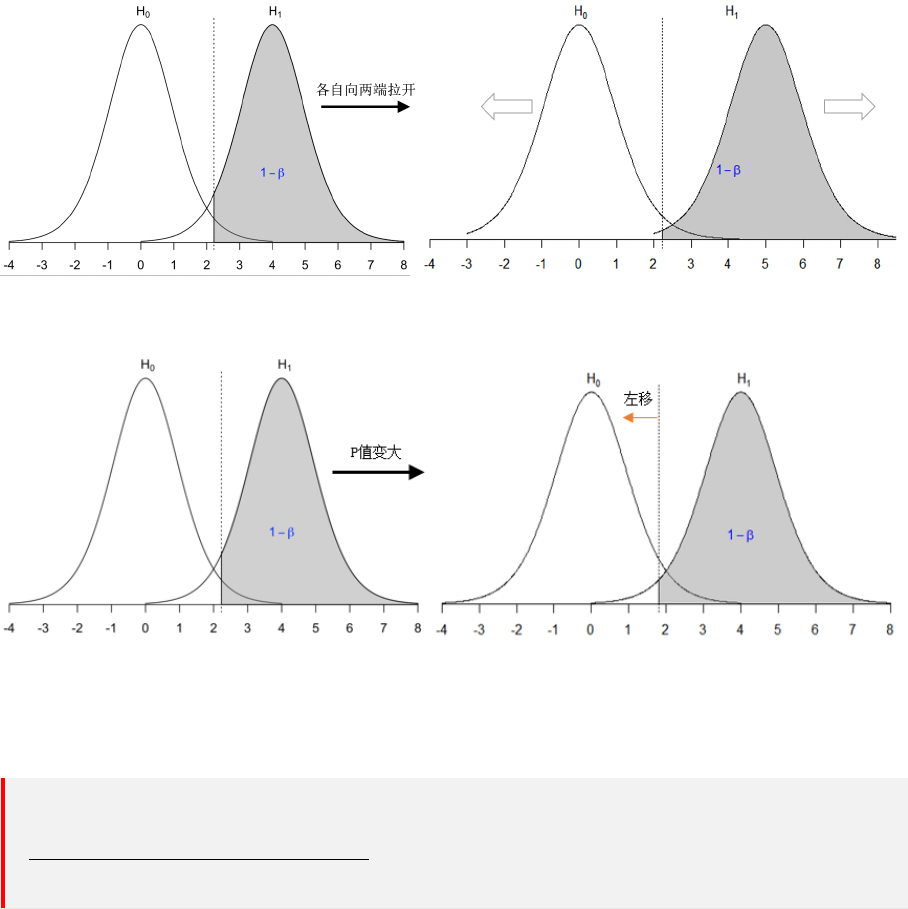
21 假设检验
图 13: 1 − β and eect size
图 14: 1 − β and P 值
α 错误又称为第一类错误,β 错误又称为第二类错误。
Note: H
0
与 H
1
是对立事件,即 H
0
发生等价于 H
1
不发生。犯弃真错误的最大
a
概率
是 α,而 α 又称为显著性水平,犯取伪错误的概率是 β。
a
注意 α 是最大的概率,实际上拒绝 H
0
时,犯弃真错误的概率真实值是 P 值。
我们希望犯这两类错误的概率越小越好。遗憾的是,在样本容量给定的情况下要想同时缩小犯
这两类错误的概率是不可能的,当其中一个减小时,另一个就会增大,见图16。
而当增大样本容量,分布的方差会被缩小,也就是分布会变“瘦”,这样量分布的交集变小,那
么两类错误的概率都被缩小了。注意的是,这里所说的分布是抽样分布,不是经验分布。经验分
布随着样本量的增加会逼近总体分布,它的离散程度不会随着样本量的增大而减小。
▷ 假设有一组 A 数据服从 (a) 分布,(a) 分布是已知的,现在我们怀疑这组数据混杂了其它
分布的数据。
▷ 假定这组数据的确是混杂了其它分布的数据,同时假定混杂进来的数据的分布为 (b)。一
般来说,我们并不知道 (b) 分布具体形式。
根据我们的假定,(a) 分布和 (b) 分布一定会有交集,没交集就不会混合。
C 事件的取值范围是 [0,5],D 事件的取值范围是 [10,15],总不能说,在 C 事件的数
据中可能混杂了 D 事件的数据。原本是 [0,5] 范围的数据,结果出来一个属于 [10,15]
的数据,这根本就不需要进行检验,就可以知道数据有问题。所以,要混合,一定要
交集非空。
显然,图中的两个分布是有交集的。如果我们要使犯弃真错误的概率减小,也就是要使 α 值减
小。那么拒绝域就要变小(中间那条竖线向右移动),但与此同时,β 值增大。
既然两类错误的概率不能同时减小,那我们要先控制那类错误出现的概率呢,弃真还是取伪?
67

21 假设检验
图 15: 1 − β 和 P 值的关系
H
0
为真 H
1
为真
没有拒绝 H
0
正确 取伪错误(β 错误)
拒绝 H
0
弃真错误(α 错误) 正确
一些入门教材会这样说先控制 α 错误,α 错误比较严重。但这完全是忽悠读者的说法。在假设检
验中有两类错误,但因为一些限制,在进行假设检验时我们只能完美控制其中一种错误的概率。
最后,我们把我们所想要控制的错误概率称为 α 值。α 是一个概率值,之所以能完美控制 α 值,
是因为 (a) 分布已知。假如 (b) 分布也是已知的,我们可以选择控制 β 错误,但要注意的是,原
来 β 错误就会被称为 α 错误。
这也说明了为什么在提出假设时,要把等号(=)放在原假设,因为原假设对应 α 错误,其分布
必须要已知。
用司法程序中的 “凭证定罪、疑罪从无” 之类的观点来理解 α 错误是没必要且错误
的。
21.4 P 值
P 值是与 α 值配对出现的概念,这是因为必须让 α 值与 P 值进行比较,才能完成假设检验。
P 值是在 H
0
成立的条件下,当前事件发生的概率(当前事件是指:出现当前样本值或更
7
极端
样本值的情况)。很容易看出,P 值就是一个条件概率。设 A 表示当前事件,则:
P = P (A|H
0
) =
P (A, H
0
)
P (H
0
)
我们人为划分出了拒绝域,实验结果落在拒绝域的概率是 α。如果 P ≤ α,那么我们拒绝 H
0
,
此时会称检验结果是显著的;如果 P > α ,那么检验结果不显著,我们没有充分的把握拒绝 H
0
,
只能接受。我们会希望 P 值尽可能地小,因为 P 值越小,检验结果越显著
8
,也就是犯弃真错
误的概率越小。
21.4.1 P 值危机
在近十多年来,很多学界,特别是在科学领域,有很多文章讨论传统统计检定方法、尤其是 P 值
统计检定的问题,甚至有位很有名的统计学者 Andrew Gelman 写了篇文章,叫作 The Statistical
7
与当前样本值相比
8
可以看出,统计学中显著是把握很大,或是可能性很大的意思。
68
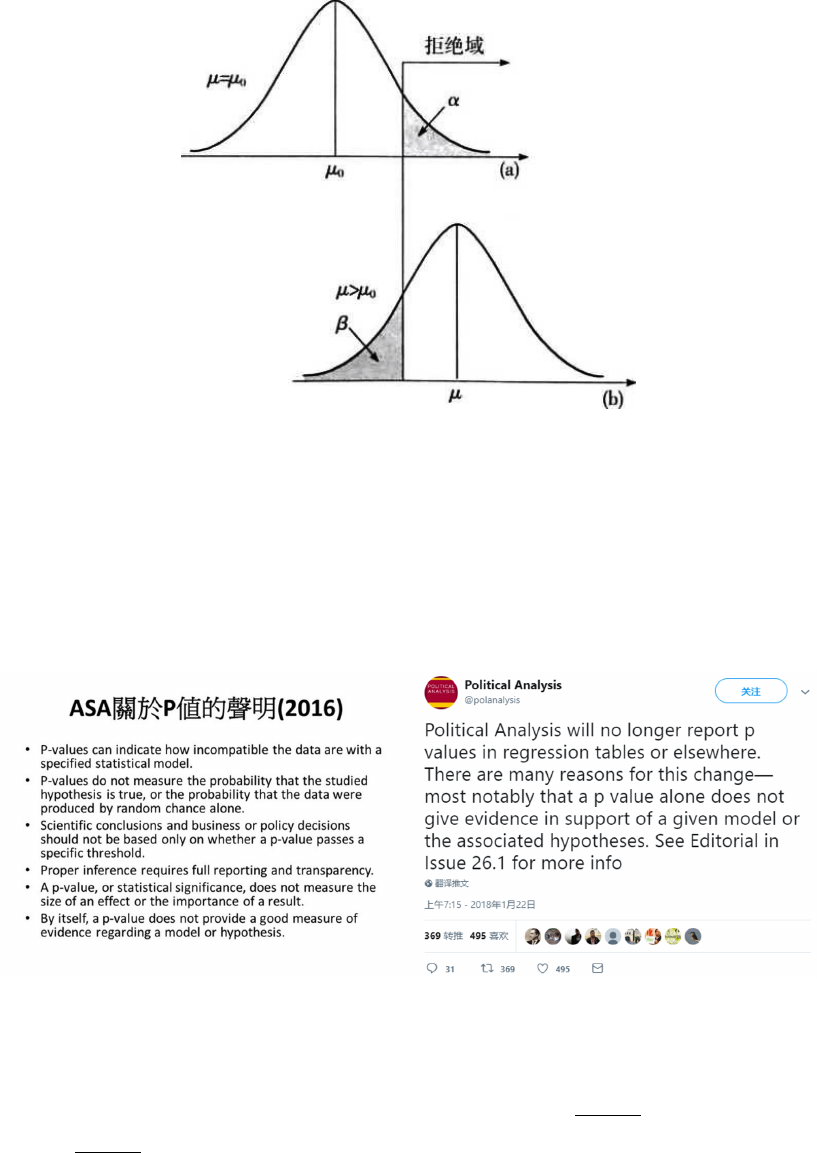
21 假设检验
图 16: α 错误、β 错误
Crisis in Science–「科学的统计学危机」,说是危机一点都不言过其实。
有些学术期刊,已经开始改变他们的编辑政策。像心理学期刊 Basic and Applied Social Psychol-
ogy,在 2016 年决定以后文章都不能使用 P 值。又比如美国政治学顶级学术期刊《政治分析》
在他们的官方 twitter 上宣布从 2018 年开始的第 26 辑起禁用 p 值,该刊认为:“p 值本身无法
提供支持相关模式或假说之证据。”
图 17: ASA、political analysis 的声明
P
值缺陷
先来收一下 P 值(或者说假设检验的缺陷性),上面说到了 P =
P (A,H
0
)
P (H
0
)
,也就是在假设检验中
我们得到了
P (A,H
0
)
P (H
0
)
的值,这个值是在假设 H
0
成立的条件下得到的,但问题是 P 值并没有告
诉我们 H
0
成立的概率有多大,也就是我们不能从 P 值得知 P (H
0
) 的值。
这里需要借助贝叶斯公式,实际上,以下的例子在贝叶斯公式的学习中很常见,如果你与贝叶斯
公式相识不久,你一定会对例子所说的感到惊讶,但对贝叶斯公式的理解可能并没有什么帮助,
因为这些例子是反直觉的,会带来很大的困扰。实际上,下面的例子或许更应该用来解释假设检
验。
假设有一天医生给了你一份蜥蜴流感诊断书,诊断结果显示为阳性。同时,你得知医
院的蜥蜴流感试验正确率为 95%。
这里,正确率为 95% 的含义是:若某人已患蜥蜴流感,试验结果为阳性的概率为 95%;
若某人未患蜥蜴流感.试验结果为阴性的概率为 95%。见下表:
没有统计学背景的人可能认为,此时患病的概应该相当大了。上表也给出了患病与非患病的先
69
21 假设检验
sick Not sick
Positive+ P (+|sick)=.95 P (+|Not sick)=.05
negative- P (−|sick)=.05 P (−|Not sick)=.95
Prior Probability P (sick)=.06 P (Not sick)=.94
验概率,根据贝叶斯公式,可以算出在诊断为阳性的情况下,实际没患病的概率是多少,即:
P (N ot sick|+) = 1 − P (sick|+) = 1 −
P (sick)P (+|sick)
P (+)
∵ P (+) = P (sick)P (+|sick) + P (Not sick)P (+|Not sick)
∴ P (N ot sick|+) = 1 −
0.06 × 0.95
0.06 × 0.95 + 0.94 × 0.05
≈ 0.45
使用贝叶斯定理算出来的结果大家应该会觉得很诧异,因为我们药物检查的工具应该是很准确
的,0.95 在我们想象中应该是很准确的,我们认为我们错误的可能性只有 5%,其实不然。因为
0.95 是一个条件概率,如果它的先验事件没有发生,这个条件事件也就不会发生。而此时,sick
的先验概率 P (sick) 相当小,只有 0.06。这就是原因所在。
现在把这个例子转换为假设检验:
H
0
:你确实患了蜥蜴流感。
H
1
:你没有患蜥蜴流感。
在 H
0
成立的条件下,被诊断为阳性的概率是 0.95。此时 α 值为 0.05。
H
0
is true H
1
is true
Not rejected H
0
P (T |H
0
)=.95 P (F |H
1
)=.05
rejected H
0
P (F |H
0
)=.05 P (T |H
1
)=.95
Prior Probability P (H
0
)=.06 P (H
1
)=.94
医院检查试验:诊断为阳性 ⇒ P > α
检验结果不显著,于是,医生认为你很可能得了蜥蜴流感。
当然,假设检验的假设形式可以互换,可以发现得到的结论是不变的。
H
0
:你没有患蜥蜴流感。
H
1
:你确实患了蜥蜴流感。
在 H
0
成立的条件下,被诊断为阳性的概率是 0.05。此时 α 值为 0.05。
H
0
is true H
1
is true
Not rejected H
0
P (T |H
0
)=.95 P (F |H
1
)=.05
rejected H
0
P (F |H
0
)=.05 P (T |H
1
)=.95
Prior Probability P (H
0
)=.94 P (H
1
)=.06
医院检查试验:诊断为阳性 ⇒ P ≤ α
检验结果显著,于是,医生认为你的确得了蜥蜴流感。
原则上,应该采取第一种假设方式,即将患病假设放在
H
0
,因为倘若患病,却推翻
H
0
,后果是
很严重的,我们肯定选择先控制“若患病,却推翻 H
0
”的概率。但实际上,两种检验形式得到
的结果一致,也就是无论将患病假设放在 H
0
还是 H
1
,检验结果都是错误的。根本原因就是其
中一类的先验概率非常小。
70
22 抽样分布、参数估计、假设检验的联系
以第二种假设方式为例子,H
0
代表阴性 −;H
1
为阳性 +。那么,当前试验的先验概率 P (H
1
)
与伪阳性的逆概率(此时为 α 的真实值)的关系如下表 [7]。
可以发现,当 power 或研究假设的先验机率(这里是 P (H
1
))甚低的时候,α = 0.05 可能严重
低估了伪阳性的逆概率,也就是在 P 值检定显著的情况下,H
0
仍然极有可能为真,而其为真的
条件机率可能甚大于 α。此时如果我们拒绝 H
0
,便作出了错误的统计推论。
原则上,power 对于伪阳性逆概率的作用不是那么强,作用强的是 prior,即是研究假设的先
验机率。当 P (H
1
) < 0.3 时,伪阳性逆概率(α 的真实值)与预定的 α 值偏离非常大。可以
看到,当 P (H
0
) = P (H
1
) = 0.5 时是最好的,但 |P (H
0
) − P (H
1
)| ≤ 0.2 也还可以接受,而
|P (H
0
) − P (H
1
)| ≥ 0.4 时,已经相当糟糕。
Note: 总结一下 P 值(假设检验)的缺陷:
1. 只能控制其中一类错误的概率。
2. P 值是 H
0
成立时,α 错误的概率。但没有告诉我们,H
0
成立的概率有多大。
(a) 当(统计效力较小(分布混合较严重))先验概率 P (H
0
) 很小时,不拒绝 H
0
实
际出错的概率很大。
(b) 当(统计效力较小(分布混合较严重))先验概率 P (H
1
) 很小时,拒绝 H
0
实
际出错的概率很大。
简而言之,P 值的问题在于:我们把 P 值设置得很小,但 α 错误的概率是不是真的如 P
值这么小?
P 值误用
多次试验,只关心结果显著的试验。这就是——摘樱桃问题。
22 抽样分布、参数估计、假设检验的联系
统计量的分布称为抽样分布。而统计量本身不包含未知参数 θ,但它的分布却包含未知参数 θ。
而枢轴量本身包含未知参数 θ,而分布已知。实际上,枢轴量和统计量有点类似互逆的关系。对
统计量配于未知参数 θ 进行变形,得到一个新的量,使得新的量的分布不包含未知参数 θ,即分
布已知。而这个量就是枢轴量。也就是说,枢轴量的分布是基于统计量的分布(抽样分布)的。
枢轴量用于区间估计,而构造区间估计的方法有两种:一是从点估计入手,二是从假设检验入手。
区间估计看起来与假设检验很相似,因为假设检验所用的检验统计量很多时候就是相应的枢轴
量,所以区间估计与假设检验有着相同的出发点。虽然枢轴量本身包含未知参数 θ,但原假设却
71

23 概念基础
对 θ 的取值进行了假定。在原假设成立的条件下,枢轴量不再包含未知量,其分布也是已知的。
另外,虽然矩估计、极大似然估计是点估计的方法,但是区间估计有时会从点估计量入手构造枢
轴量。当这个点估计量是样本的函数(矩估计等)时,区间估计也就是从统计量入手构造枢轴量。
23 概念基础
23.1 统计量的极限分布、大样本与小样本
当样本大小趋于无穷时,若统计量的分布趋于一定的分布,则后者称为该统计量的极限分布或渐
近分布,也常称为大样本分布。这可以理解为:当样本大小很大时统计量的近似分布。
统计量的极限分布,或者更广一些,有关当样本大小趋于无穷时统计量的极限性质的研究,其意
义有两个方面。首先,如前面指出的要弄清楚一统计推断方法的优良性如何,甚至单纯为了实施
这个推断方法,往往有必要知道统计量的分布。但后者一般很难求出,建立其极限分布,就提供
了一种近似解法的可能性在其次,统计推断方法的某些优良性准则。本身就是建立在样本大小
趋于无穷的基础上。
当样本大小趋于无穷时,一个统计量或者统计推断方法的性质,称为大样本性质。大样本性质只
有在样本大小趋于无穷时才有意义。与此相对,统计量或者统计推断方法的某一性质,如果在样
本大小固定时有意义,就称为小样本性质。在此要强调的是,大样本和小样本的差别不在于样本
个的多少,而在于:问题是在样本大小 n → ∞ 时去讨论,还是 n 固定时去讨论。关于大样本性
质的研究构成数理统计学的一个很重要的部分,叫大样本统计理论。近几十年来得到很大的发
展,成为战后数理统计发展的特点之一。有些统计分支,例如非参数统计,其中大样本理论占据
了主导的地位。
23.2 充分统计量
统计量的一个作用,是把样本中有用的信息集中起来。一个统计量能集中样本里的多少信息,自
与统计量的具体形式有关,但也依赖于问题的统计模型
9
。最好的情况是:统计量把样本中的全
部信息都包含进来了。换句话说只要算出了这个统计量的值,就是把原始样本丢掉了,也无任何
损失。满足这种条件的统计量就叫做充分统计量,现在我们来设法给这个直观论述以严格的数
学解释,从而引出充分统计量的正式定义。
记样本 X
1
, ··· , X
m
为 X。设有统计量 T = T (X)。我们可 以把得出样本 X 的过程看成是由两
步实现的:第一步观察 T 。第 二步在已知 T 的条件下去观察 X。整个样本中所含的(有关 X
的样本分布的参数 θ 的)信息,是这两步所提供的信息的和。第 一步的信息就是统计量 T 所包
含的信息。因此,当且仅当第二步 所提供的信息为 0 时,统计量才是充分的。但第二步所提供
的信息 是否为 0,又取决于在已知的条件的条件分布是否与参数 θ 无关。因为,倘若这条件分
布与 θ 无关,则在已知 T 时进一步 去观察属相当于去观察一个与 θ 毫无关系的量。其中当然
不包 含关于 θ 的信息。反之,若这条件分布与 θ 有关,则在已知 T 时 观察还可以提供一些关
于 θ 的信息。这样,可以给出充分统计 量的正式定义如下。
定义23.1 充分统计量:设 x
1
, x
2
, . . . , x
n
是来自某个总体的样本,样本的分布族为 F (x; θ), θ ∈
Θ,如果在给定 T 的取值后,样本 x
1
, x
2
, . . . , x
n
的条件分布与 θ 无关。则称统计量 T =
T (x
1
, x
2
, . . . , x
n
) 为 θ 的充分统计量。
23.3 参数估计
推断总体的前提是拥有样本,如果没有样本,统计推断没有任何意义。仅当样本是简单随机样
本,样本分布才由总体分布决定。
9
参看《数理统计学教程》陈希孺,例 1.25 中的说明
72
23 概念基础
23.3.1 点估计
点估计是数理统计学中内容很丰富的一个分支。它主要包括 制定估计量的一般方法,制定有关
估计量优良性的种种合理准则,寻求某种特定准则下的最优估计量,以及记明某一特定的估计量
(用直观方法或某种一般性方法得到的)在某种准则之下有最优性 等等。
23.3.2 极大似然估计
设样本 X(不一定是简单随机样本)有概率函数 f(x, θ)。这里 θ 为参数,在参数空间 Θ 内取
值。当固定 x 而把 f(x, θ),看成是 θ 的定义在 Θ 上的函数时,它称为似然函数。
所以概率函数与似然函数可以说是一回事,只是看法不同:前者是固定 θ 而看成是在样本空间
Ω 上的函数,后者则固定 θ 而看成是在 Θ 的函数。这个差别在统计上的意义如下:不妨把参 θ
和样本 x 分别看成是“原因”和“结果”。定了 θ 的值,就完全确定了样本分布,也就定下了得
到种种结果 x 的机会大小。这是从正面看,从反面看,当有了结果样(样本 x)时,我们问:当
参数 θ 取各种不同的值(原因时,导出这个结果 x 的可能性有多大?这个问题的回答引出似然
函数的概念。“似然”的字面意义就是“看起来象”。说仔细一些,就是当我们有了结果时,这结
果看来是由原因 θ 而产生的可能性,与似然函数值 f(x, θ) 成比例。由于统计推断是由样本推断
参数,这个看法就可以作为一种统计推断方法的哲理基础。事实上,确有一些统计学家作这样的
主张,它们把基于每个参数值的“似然性”去进行统计推断这个原则,叫做似然 原则。应当注
意的是:反映 θ 的似然性的 f (x, θ),虽然是源出于 一个概率论概念——概率函数,本身并不是
通常意义下的概率它自然也没有频率解释。
23.3.3 矩估计与极大似然估计
矩估计和极大似然估计是两种基本的点估计方法。从大样本的观点看,似然估计一般优于点估
计。以此之故,它受到更大的重视,但矩估计也有其优点,一则它对样 本分布形式要求少。在
极大似然估计的情况,概率函数须有简单的解析表达式,参数 θ 也需取值于欧氏空间。对矩估
计则无这类限制。另外在矩估计法能用的场合,其计算一般比极大似然估计简单些。
23.3.4 区间估计
置信水平和置信系数的概念是 Neyman 区间估计理论的基本概念。这个概念的要点在于:被估
计的参数 θ 虽然未知但是是一个常数,没有随机性,而区间 [θ
1
(X), θ
2
(X)] 则是随机的。因此,
这个概念允许一种频率的解释:如果把这个区间估计反复使用许多次,则有时它包含免有时不
包含,当次数充分大时,包含的频率接近于置信系数。因此, 一个置信系数为 0.95 的区间估计
[θ
1
(X), θ
2
(X)],其实际意义可理解为:当把 [θ
1
(X), θ
2
(X)] 使用 100 次时,平均约有 95 次,其
结果是正确的,即包含了被估计的 θ。
构造置信区间的方法主要有两种:一种是从点估计出发,一种是从假设检验出发。在一些常见的
重要问题中,这两种方法往往给出同一结果。
区间估计和假设检验之间有很密切的关系,这种关系不止是形式上的。事实上,某种准则下的最
优检验,往往导致相应准则下的最优区间估计,反之亦然。
与点估计和假设检验比较,区间估计这种推断形式有一个显著的特点,即它的精度(一般可用区
间的长度刻划)和可靠度(用其置信系数刻划)一目了然。有如本章开始时指出的:正是因为点
估计不具备这个特点,才使人们考虑区间估计,假设检验也有这个问题。
73
23 概念基础
74
参考文献
[1] 嚴加安. 概率破玄機 統計解迷離. 數學傳播, 38(2):23–34, 2014.
[2] 孙伟. 论数学期望定义中“绝对收敛”. 哈尔滨金融高等专科学校学报, 3:030, 2008.
[3] 张永利. 矩估计的基本原理及其解题方法. 巢湖学院学报, 7(3):47–49, 2005.
[4] 战立侃. 72 位著名科学家呼吁提高统计显著性水平以提升科学研究的可重复性, 2017.
[5] 战立侃. 正确理解和使用 p 值, 2017.
[6] 战立侃. 统计的显著性水平, 2017.
[7] 林泽民. 看电影学统计: p 值的陷阱. 社会科学论丛, 10(2), 2016.
[8] 茆诗松 程依明 濮晓龙. 概率论与数理统计教程 (第二版). 北京: 高等教育出版社, 2011.
[9] 熊锐. 测度论基础.
[10] 谢益辉. 现代统计图形. 2010.
[11] 連怡斌. 由「太陽從西邊升起」談 p 值的意義. 數學傳播, 42(3):43–47, 2018.
[12] 陈家鼎, 孙山泽, 李东风, and 刘力平. 数理统计学讲义. 高等教育出版社, 2015.
[13] 陈希儒. 概率论与数理统计. 中国科技大学出版社, 1992.
[14] 陈希孺. 数理统计引论. 科学出版社, 1981.
[15] 陈希孺 and 倪国熙. 数理统计学教程. 上海科学技术出版社, 1988.
[16] 黃文璋. 機率應用不易. 數學傳播, 34(1):14–28, 2010.
75
