机器学习
siwing
2020 年 10 月 13 日
2
目录
第一部分 模型选择与评估 1
第一章 概述 3
1.1 基本概念 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
1.2 假设空间 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
1.2.1 线性模型 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
1.2.2 非线性模型 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
1.3
学习准则
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
1.3.1 风险最小化准则 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
1.3.2 结构风险最小化准则 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
第二章 评估假设空间 7
2.1 模型的参数和超参数 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
2.2 偏差-方差分解 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
2.3 交叉验证 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
2.3.1 简单交叉验证 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
2.3.2 K 折交叉验证 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
2.3.3 留一法和留 P 法 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
2.3.4 时序交叉验证 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11
第三章 评估模型 13
3.1 回归 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13
3.1.1 均方误差 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13
3.2 分类 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13
3.2.1 混淆矩阵 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13
3.2.2 Error Rate
与
accuracy . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14
3.2.3 Precision、Recall . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15
3.2.4 TPR、FPR . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17
3.2.5 ROC、AUC . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17
3
目录
3.2.6 代价敏感错误率 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
第四章 信息熵 * 21
第二部分 机器学习中阶
传统模型 23
第五章 决策树 25
5.1 简介 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25
5.2 决策树基本算法 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26
5.3 划分选择 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26
5.3.1 信息增益 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27
5.3.2 信息增益比 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28
5.3.3 基尼指数 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29
5.4 连续值处理 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29
5.5 缺失值处理 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30
5.6 剪枝 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31
5.6.1 预剪枝 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31
5.6.2 后剪枝 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31
5.6.2.1 错误率降低剪枝 (Reduced-Error Pruning, REP) . . . . . . . . . 31
5.6.2.2 悲观错误剪枝 (Pessimistic Error Pruning, PEP) . . . . . . . . . 32
5.6.2.3 代价复杂度剪枝 (Cost-Complexity Pruning, CCP) . . . . . . . . 32
5.7 多变量决策树 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35
5.8 总结 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 36
5.9 Python 代码 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 37
第六章 Perceptron 39
6.1 损失函数 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 40
6.2 参数更新 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 41
6.3 感知器收敛性 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 43
6.4 感知机的缺陷 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 43
第三部分 机器学习高阶
优化方法 45
第七章 凸优化基础概念 47
4
目录
7.1 凸集 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 47
7.2 重要的凸集 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 48
7.3 保持凸性的运算 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 49
7.3.1 交集 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 49
7.3.2 仿射函数 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 49
第八章 梯度下降 51
8.1 梯度下降原理 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 51
第九章 Backpropagation 53
9.1 神经网络 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 53
9.2 基本函数 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 53
9.3 前向传播 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 54
9.4 反向传播 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 56
9.4.1 输出层 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 56
9.4.2 隐藏层 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 57
9.5 权值更新归纳 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 57
第四部分 神经网络 59
第十章 Perceptron 61
10.1 损失函数 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 62
10.2 参数更新 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 63
10.3 感知器收敛性 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 65
10.4 感知机的缺陷 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 65
第十一章 Recurrent Neural Networks 67
11.1 Simple Recurrent Network . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 67
11.1.1 前向传播 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 67
11.1.2 反向传播 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 69
11.1.3 title . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 70
11.2 LSTM . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 70
11.2.1 LSTM 概述 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 70
11.2.2 LSTM 与 RNN 的区别 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 70
11.2.3 遗忘门 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 71
11.2.4 输入门 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 71
5
11.2.5 细胞状态更新 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 72
11.2.6 输出门 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 72
11.3 带窥孔的 LSTM . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 72
11.4 GRU . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 72
第十二章 Seq2Seq 75
12.1 Encoder-Decoder . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 75
12.2 Seq2Seq . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 76
12.3 Attention 机制 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 77
第一部分
模型选择与评估
1

第一章 概述
1.1 基本概念
在早期的工程领域,机器学习也经常称为模式识别(Pattern Recognition,PR),但模式识别更
偏向于具体的应用任务,比如光学字符识别、语音识别、人脸识别等。这些任务的特点是,对于
我们人类而言,这些任务很容易完成,但我们不知道自己是如何做到的,因此也很难人工设计一
个计算机程序来完成这些任务。一个可行的方法是设计一个算法可以让计算机自己从有标注的
样本上学习其中的规律,并用来完成各种识别任务。随着机器学习技术的应用越来越广,现在机
器学习的概念逐渐替代模式识别,成为这一类问题及其解决方法的统称。
定义1.1 浅层学习: 传统的机器学习主要关注如何学习一个预测模型。一般需要首先将数据表
示为一组特征(Feature),特征的表示形式可以是连续的数值、离散的符号或其他形式。然后将这
些特征输入到预测模型,并输出预测结果。这类机器学习可以看作浅层学习(Shallow Learning)。
浅层学习的一个重要特点是不涉及特征学习,其特征主要靠人工经验或特征转换方法来抽取。
定义1.2 表示学习: 为了提高机器学习系统的准确率,我们希望将输入信息转换为有效的特征,
或者更一般性地称为表示(Representation)。如果有一种算法可以自动地学习出有效的特征,并
提高最终机器学习模型的性能,那么这种学习就可以叫作表示学习(Representation Learning)。
定义1.3 语义鸿沟: 表示学习的关键是解决语义鸿沟(Semantic Gap)问题。语义鸿沟问题是
指输入数据的底层特征和高层语义信息之间的不一致性和差异性。
在机器学习中,底层特征来自计算机直接记录的数据,而高层特征来自人类的观察。例如:
1. 计算机使用唯一的整数表示一个字词,如 Unicode 编码,计算机看到的底层特征只
是一个个数字。然而这些字词在人类的认知中存在更丰富的含义,如一些字词是近
义词或者反义词,不同的字词表达了不同的情绪等等。
2. 图片在计算中以一个个像素点呈现,但在人类对图片的观察是建立在比较抽象的高
层语义上的,例如,人类会根据图片中物体的颜色、形状等等特征去辨识事物。因此
为了从图像的原始数据中识别具体的场景,可能需要以适当算法对像素进行选择和
操纵,提取出高层的特征。
如果一个预测模型直接建立在底层特征之上,会导致对预测模型的能力要求过高。如果可以有
一个好的表示在某种程度上能够反映出数据的高层语义特征,那么我们就能相对容易地构建后
续的机器学习模型。在表示学习中,有两个核心问题:一是“什么是一个好的表示”;二是“如
何学习到好的表示”。
“好的表示”是一个非常主观的概念,没有一个明确的标准。但一般而言,一个好的表示具有以
下几个优点:
1. 一个好的表示应该具有很强的表示能力,即同样大小的向量可以表示-更多信息。
2. 一个好的表示应该使后续的学习任务变得简单,即需要包含更高层的语义信息。
3. 一个好的表示应该具有一般性,是任务或领域独立的。虽然目前的大部分表示学习方法还
是基于某个任务来学习,但我们期望其学到的表示可以比较容易地迁移到其他任务上。
在机器学习中,我们经常使用两种方式来表示特征:局部表示(Local Rep- resentation)和分布
3
1.2 假设空间
式表示(Distributed Representation)。
以颜色表示为例,我们可以用很多词来形容不同的颜色,除了基本的红、蓝、绿、白、黑等之外,
还有很多以地区或物品命名的,比如中国红、天蓝色、咖啡色、琥珀色等。如果要在计算机中表
示颜色,
定义1.4 局部表示: 以不同名字来命名不同的颜色,这种表示方式叫作局部表示,也称为离散
表示或符号表示。局部表示通常可以表示为 one-hot 向量的形式。
局部表示有两个优点:
1. 这种离散的表示方式具有很好的解释性,有利于人工归纳和总结特征,并通过特征组合进
行高效的特征工程。
2. 通过多种特征组合得到的表示向量通常是稀疏的二值向量,当用于线性模型时计算效率非
常高。
但局部表示有两个不足之处:
1. one-hot 向量的维数很高,且不能扩展。如果有一种新的颜色,我们就需要增加一维来表
示。
2. 不同颜色之间的相似度都为 0,即我们无法知道“红色”和“中国红”的相似度要高于“红
色”和“黑色”的相似度。
定义1.5 分布式表示: 分布式表示通常可以表示为低维的稠密向量,向量的单个维度没有意义,
各个维度组合起来才能表示具体的数据。例如,用 RGB 值来表示颜色,不同颜色对应到 R、G、
B 三维空间中一个点。
在传统的机器学习中,也有很多有关特征学习的方法,比如主成分分析、线性判别分析、独立成
分分析等。但是,传统的特征学习一般是通过人为地设计一些准则,然后根据这些准则来选取有
效的特征。特征的学习是和最终预测模型的学习分开进行的,因此学习到的特征不一定可以提
升最终模型的性能。
神经网络可以将高维的局部表示空间 R
|v|
映射到一个非常低维的分布式表示空间 R
D
, D < |v|。
在这个低维空间中,每个特征不再是坐标轴上的点,而是分散在整个低维空间中。在机器学习中,
这个过程也称为嵌入(Embedding )。嵌入通常指将一个度量空间中的一些对象映射到另一个低
维的度量空间中,并尽可能保持不同对象之间的拓扑关系。比如自然语言中词的分布式表示,也
经常叫作词嵌入。
1.2 假设空间
输入空间 X 和输出空间 y 构成了一个样本空间。对于样本空间中的样本 (x, y) ∈ X ×y,假定 x
和 y 之间的关系可以通过一个未知的真实映射函数 y = g(x) 或真实条件概率分布 p
r
(y | x) 来描
述。机器学习的目标是找到一个模型来近似真实映射函数 g (x) 或真实条件概率分布 p
r
(y | x)。
由于我们不知道真实的映射函数 g(x) 或条件概率分布 p
r
(y | x) 的具体形式,因而只能根据经
验来假设一个函数集合 F,称为假设空间(Hypothesis Space ),然后通过观测其在训练集 D 上
的特性,从中选择一个理想的假设(Hypothesis ) f
∗
∈ F。
定义1.6 假设空间: 假设空间 F 通常为一个参数化的函数族
F =
f(x; θ) | θ ∈ R
D
其中 f(x; θ) 是参数为 θ 的函数,也称为模型 (Model),D 为参数的数量。
常见的假设空间可以分为线性和非线性两种,对应的模型 f 也分别称为线性模型和非线性模型。
4
1.3 学习准则
1.2.1 线性模型
线性模型的假设空间为一个参数化的线性函数族,即
f(x; θ) = w
⊤
x + b
其中参数 θ 包含了权重向量 w 和偏置 b。
1.2.2 非线性模型
广义的非线性模型可以写为多个非线性基函数 ϕ(x) 的线性组合
f(x; θ) = w
⊤
ϕ(x) + b
其中 ϕ(x) = [ϕ
1
(x), ϕ
2
(x), ··· , ϕ
K
(x)]
⊤
为 K 个非线性基函数组成的向量,参数 θ 包含了权重
向量 w 和偏置 b。
如果 ϕ(x) 本身为可学习的基函数,比如
ϕ
k
(x) = h
w
⊤
k
ϕ
′
(x) + b
k
�∀1 ≤ k ≤ K
其中 h(·) 为非线性函数,ϕ
′
(x) 为另一组基函数,w
k
和 b
k
为可学习的参数,则 f(x; θ) 就等价
于神经网络模型。
1.3 学习准则
令训练集 D =
x
(n)
, y
(n)
N
n=1
是由 N 个独立同分布的(Identically and Independently Dis-
tributed,IID ) 样本组成,即每个样本 (x, y) ∈ X × y 是从 X 和 y 的联合空间中按照某个未知
分布 p
r
(x, y) 独立地随机产生的。这里要求样本分布 p
r
(x, y) 必须是固定的(虽然可以是未知
的),不会随时间而变化. 如果一个好的模型 f (x, θ
∗
) 应该在所有 (x, y) 的可能取值上都与真实
映射函数 y = g(x) 一致,即
|f (x, θ
∗
) − y| < ϵ, ∀(x, y) ∈ X × y
或与真实条件概率分布 p
r
(y | x) 一致,即
|f
y
(x, θ
∗
) − p
r
(y | x)| < ϵ, ∀(x, y) ∈ X × y
其中 ϵ 是一个很小的正数, f
y
(x, θ
∗
) 为模型预测的条件概率分布中 y 对应的概率。模型 f(x; θ)
的好坏可以通过期望风险 ( Expected Risk ) R(θ) 来衡量,其定义为
R(θ) = E
(x,y)∼p
r
(x,y)
[L(y, f (x; θ))]
其中 p
r
(x, y) 为真实的数据分布 , L(y, f (x; θ)) 为损失函数。损失函数用来量化两个变量之间的
差异。
1.3.1 风险最小化准则
一个好的模型 f(x; θ) 应当有一个比较小的期望错误,但由于不知道真实的数据分布和映射函数
(即不知道总体),实际上无法计算其期望风险 R(θ)。我们只可以计算经验风险 ( Empirical Risk ),
即在训练集 D =
x
(n)
, y
(n)
N
n=1
上的平均损失:
5

1.3 学习准则
R
emp
D
(θ) =
1
N
N
X
n=1
L
y
(n)
, f
x
(n)
; θ
根据大数定律,当样本数 N 趋于无穷大时,经验风险可以作为期望风险的估计。因此,一个切
实可行的学习准则是找到一组参数 θ 使得经验风险最小,即
θ
∗
= arg min
θ
R
emp
D
(θ)
这就是经验风险最小化(Empirical Risk Minimization,ERM ) 准则。
1.3.2 结构风险最小化准则
但由于训练样本往往是真实数据的一个很小的子集或者包含一定的噪声数据,不能很好地反映
全部数据的真实分布.经验风险最小化原则很容易导致模型在训练集上错误率很低,但是在未知
数据上错误率很高.这就是过拟合(Overtting )。
定义1.7 过拟合: 给定一个假设空间 F,一个假设 f 属于 F,如果存在其他的假设 f
′
也属于
F,使得在训练集上 f 的损失比 f
′
的损失小,但在整个样本空间上 f
′
的损失比 f 的损失小, 那
么就说假设 f 过度拟合训练数据 [Mitchell, 1997]。
过拟合问题往往是由于训练数据少和噪声以及模型能力强等原因造成的。为了解决过拟合问题,
一般在经验风险最小化的基础上再引入参数的正则化(Regularization)来限制模型能力,使其不
要过度地最小化经验风险。这种准则就是结构风险最小化(Structure Risk Minimization,SRM)
准则:
θ
∗
= arg min
θ
R
struct
D
(θ)
= arg min
θ
R
emp
D
(θ) +
1
2
λ∥θ∥
2
= arg min
θ
1
N
N
X
n
=1
L
y
(n)
, f
x
(n)
; θ
+
1
2
λ∥θ∥
2
其中 ∥θ∥ 是 ℓ
2
范数的正则化项,用来减少参数空间,避免过拟合;λ 用来控制正则化的强度。
因为引入了正则项,当模型的参数越多,模型越复杂,正则项的值就会越大,这样就会迫
使模型在学习时不会选择过多的参数。因此这是对模型复杂度的惩罚机制。
正则化项也可以使用其他函数,比如 ℓ
1
范数. ℓ
1
范数的引入通常会使得参数有一定稀疏性,因
此在很多算法中也经常使用。从贝叶斯学习的角度来讲,正则化是引入了参数的先验分布,使其
不完全依赖训练数据。
6
第二章 评估假设空间
2.1 模型的参数和超参数
参数(parameter)和超参数(hyperparameter)在文献中常被混为一谈。研究者经常提到的“调
参”,实际上是调整超参数。为了防止语言上的混淆,我们首先对两者进行界定。
参数是模型的内部变量,是模型通过学习可以确定的参数。以简单的一元线性回归模型 y = kx+b
为例,斜率 k 和截距 b 是该模型的参数。支持向量机模型的支持向量,神经网络模型的神经元连
接权值都是模型的参数。对于决策树类的模型而言,每一步分裂的规则也属于模型参数的范畴。
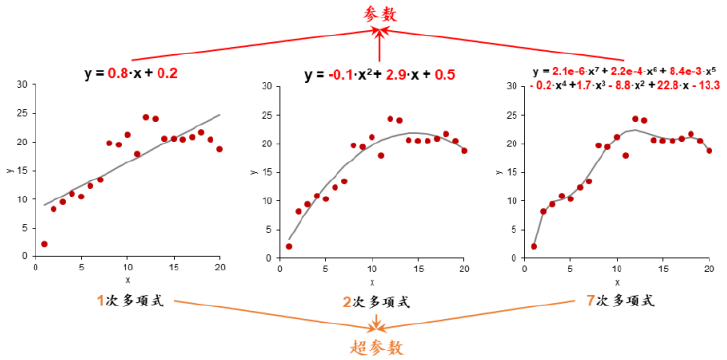
超参数是模型的外部变量,是使用者用来确定假设空间的参数。假设我们希望采用回归模型对一
组自变量 x 和因变量 y 进行拟合,究竟使用线性(一次)模型 y = kx+b、二次模型 y = k
2
x
+k
2
x+ b、
三次模型 y = k
1
x
3
+ k
2
x
2
+ k
3
x + b 或者更高次的回归模型,这里的多项式次数就是模型的超参
数。下图展示了对回归模型中参数和超参数的辨析。
图 2.1: 超参数和参数
支持向量机模型中核函数类型、惩罚系数等,随机森林模型的树棵数、最大特征数、剪枝参数等,
XGBoost 模型的学习率、最大树深度、行采样比例等、神经网络模型的网络层数、神经元个数、
激活函数类型等,这些都属于模型的超参数。
模型的参数可以从训练集学习到,模型的超参数无法从训练集中直接学习到。模型的超参数应
如何学习?在解答这一问题之前,首先要介绍模型超参数选择不当导致的问题——欠拟合和过拟
合。
2.2 偏差-方差分解
定义2.1 误差 (error): 样本的真实值与预测结果之间的差异。
7
2.2 偏差-方差分解
训练误差 (training error):在训练集上的误差,又称为经验误差(empirical error)
测试误差(test error):在测试集上的误差。
泛化误差(generalization error):在所有新样本上的误差,即测试误差(测试集的样本都
是新样本)。
训练误差很小是没什么用的,我们希望得到在新样本上表现得很好的学习器,即泛化误差小的学
习器。因此,我们应该让学习器尽可能地从训练集中学出普适性的“一般特征”,这样在遇到新
样本时才能做出正确的判别。然而,当学习器把训练集学得“太好”的时候,即把一些训练样本
的自身特点当做了普遍特征;同时也有学习能力不足的情况,即训练集的基本特征都没有学习出
来。我们定义:
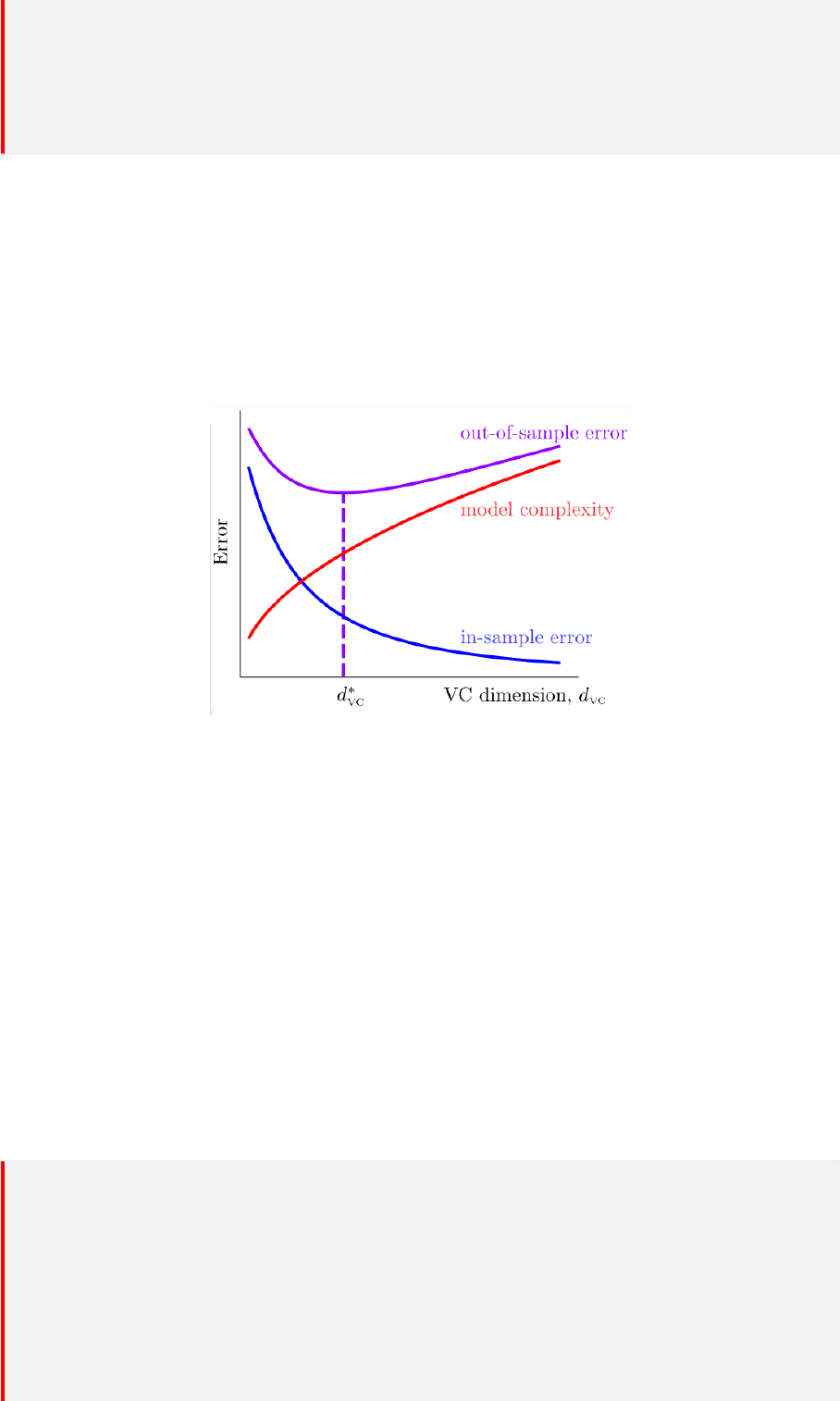
过拟合(overtting):当训练误差减小,测试误差增大,则存在过拟合。
欠拟合(undertting):训练误差和测试误差都在减小,则存在欠拟合。
图 2.2: 欠拟合与过拟合
可以得知:在过拟合问题中,训练误差十分小,但测试误差教大;在欠拟合问题中,训练误差和
测试误差都比较大。目前,欠拟合问题比较容易克服,例如增加迭代次数等,但过拟合问题还没
有十分好的解决方案,过拟合是机器学习面临的关键障碍。
对于一般的回归问题,如果我们假设 Y = f(X) + ϵ,其中 E(ϵ) = 0,并且 Var(ϵ) = σ
2
ϵ
。如果使用
均方误差(mean squared error,MSE)来衡量模型拟合程度的优劣的情况下,在输入点 X = x
0
处,回归拟合值
ˆ
f(X) 的均方误差:
MSE (x
0
) = E
Y −
ˆ
f (x
0
)
2
|X = x
0
= σ
2
ε
+
h
E
ˆ
f (x
0
) − f (x
0
)
i
2
+ E
h
ˆ
f (x
0
) − E
ˆ
f (x
0
)
i
2
= σ
2
ε
+ Bias
2
ˆ
f (x
0
)
+ Var
ˆ
f (x
0
)
= Irreducible Error + Bias
2
+ Variance
(2.1)
注意,输入点 X = x
0
是固定的,Y = f (X
0
) + ϵ = Y
0
,Y 也是固定的,即常数。而不固定
的是
ˆ
f(x
0
),显然
ˆ
f(x
0
) 不固定的原因是
ˆ
f 是不固定的。
ˆ
f 不固定的原因可能是训练集的
不同(训练集不同会导致模型参数取值不同),或者模型的假设空间不同。但在这里,只能
是训练集的不同,因为 MSE(x
0
) 用于评估模型的过拟合和欠拟合情况,假设空间必须是
固定的。
很多资料在推导均方误差分解公式时,并没有指明 Y 是常数,或者将 Y = f(X) 描述为一
个确定的函数,这是造成 MSE 困惑的原因。实际上,确定的函数(参数确定的函数)并
不意味着 Y 值是确定的,Y 值是否是常数,还取决于 x 值是否给定。
8
2.2 偏差-方差分解
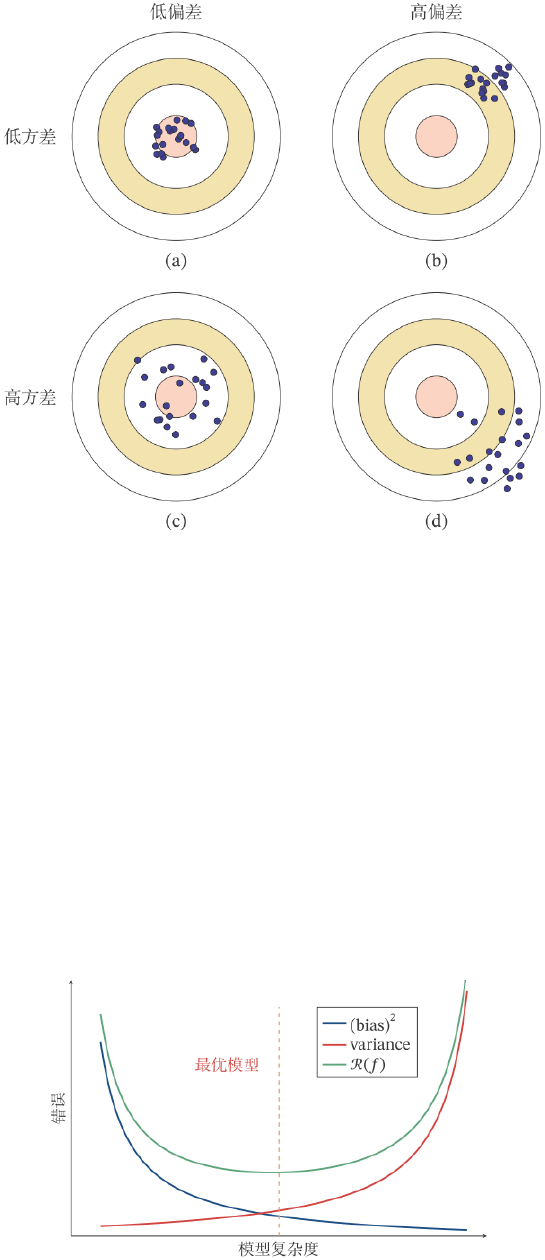
Variance 是指一个模型在不同训练集上的差异,可以用来衡量一个模型是否容易过拟合;Bias
2
代表一个模型在不同训练集上的平均性能和最优模型的差异,可以用来衡量一个模型的拟合能
力。
图 2.3: 机器学习模型的四种偏差和方差组合情况
进一步看,Variance 代表我们使用不同训练集时模型表现的差异。由于模型的构建通常和训练
集的统计性质有关,不同的训练集会导致模型出现差异。如果某个机器学习方法得到的模型具有
较大的方差,训练集只要有少许变化,模型会有很大的改变。复杂的模型一般具有更大的方差。
第二项偏差代表实际模型与理想模型的差别。例如线性模型是最常用的模型之一,而真实世界往
往是非常复杂的,当我们用线性模型这样的简单模型去解释世界时,很可能会出现问题。如果我
们用复杂度为 2 的线性模型(包含截距和斜率两个参数)拟合一个非线性模型(模型复杂度远大
于 2),将产生较大的均方误差,其中很大一部分来源于偏差,这种情况称为欠拟合(undertting)。
当我们不断增加模型的复杂程度,模型的均方误差不断下降,整体表现逐渐提升,主要原因是偏
差逐渐下降,说明模型更加符合真实的情况。然而随着模型的复杂程度进一步增加,可以发现样
本差异导致的方差急剧上升,说明复杂的模型更多地把握住了属于训练样本独有的特性,而非数
据的共性,这种情况称为过拟合(overtting)。均方误差、方差和偏差随模型复杂度的变化关系
如下图所示。
图 2.4: 均方误差、方差和偏差随模型复杂度的变化关系(模型的函数空间不同)
偏差和方差分解给机器学习模型提供了一种分析途径。但在实际操作中难以直接衡量.一般来
说。当一个模型在训练集上的错误率比较高时。说明模型的拟合能力不够。偏差比较高.这种情
况可以通过增加数据特征、提高模型复杂度、减小正则化系数等操作来改进.当模型在训练集上
9

2.3 交叉验证
的错误率比较低。但验证集上的错误率比较高时。说明模型过拟合。方差比较高.这种情况可以
通过降低模型复杂度、加大正则化系数、引入先验等方法来缓解.此外。还有一种有效降低方差
的方法为集成模型。即通过多个高方差模型的平均来降低方差.
2.3 交叉验证
避免过拟合的重要方法之一是进行交叉验证(cross-validation)。英国统计学家 Mervyn Stone 和
美国统计学家 Seymour Geisser 是交叉验证理论的先驱。交叉验证理论并非仅针对机器学习模
型。而是针对任何统计模型。Stone 和 Geisser 在 1974 年分别独立地提出。在评价某个统计模型
的表现时。应使用在估计模型环节未使用过的数据。随后 Devijver Pierre(1982)、Kohavi Ron
(1995)等将交叉验证的思想引入模式识别以及机器学习。在评价机器学习模型表现时。使用不
曾在训练环节出现过的样本进行验证。如果模型在验证时性能和训练时大致相同。那么就可以
确信模型真的“学会”了如何发现数据中的一般规律。而不是“记住”训练样本。这和学生考试
的情形类似。要想考察学生是否掌握了某个知识点。不能使用课堂上讲过的“例题”。而应当使
用相似的“习题”。
交叉验证的核心思想是先将全部样本划分成两部分。一部分用来训练模型。称为训练集;另外一
部分用来验证模型。称为验证集。随后考察模型在训练集和验证集的表现是否接近。如果两者接
近。说明模型具备较好的预测性能;如果训练集的表现远优于验证集。说明模型存在过拟合的风
险。
当我们需要对不同超参数设置下的多个模型进行比较时。可以考察模型在验证集的表现。选择
验证集表现最优的那组超参数作为最终模型的超参数。这一过程称为调参(parameter tuning)。
虽然名为“调参”。本质上是“调超参”。
根据训练集和验证集的划分方式。交叉验证方法又可以细分为简单交叉验证、K 折交叉验证、留
一法、留 P 法和时序交叉验证。
2.3.1 简单交叉验证
从总样本中随机选取一定比例(如 30%)的样本作为验证集。其余作为训练集。这种方法称为
简单交叉验证。也称为留出法交叉验证(hold-out cross-validation)。
优点: 1 只需要训练一次模型。速度较快。
缺点: 1 一部分数据从未参与训练。可能削弱模型的准确性。在极端情况下。当验证集中数据本
身就是整体数据的“噪点”时。模型的准确度将会大大降低。 2 最终的模型评价结果可能受到训
练集和验证集划分过程中的随机因素干扰。
2.3.2 K 折交叉验证
针对简单交叉验证的缺陷。研究者提出 K 折交互验证(K-fold cross-validation)的方法。随机将
全体样本分为 K 个部分。每次用其中的一部分作为验证集。其余部分作为训练集。重复 K 次。
直到所有部分都被验证过。下图展示了 5 折交互验证的过程。将全体样本随机划分成 5 个不重
叠的部分。每次用 4/5 作为训练集(粉色部分)。其余 1/5 部分作为验证集(灰色部分)。最终
将得到 5 个验证集的均方误差(或其它损失函数形式)。取均值作为验证集的平均表现。
2.3.3 留一法和留
P
法
除了将样本分成 K 个部分。还可以每次取一个固定数目的样本作为验证集。假设样本量为 N。
如果每次取一个样本验证。把其余样本用来训练。重复 N 次。这种方法称为留一法交叉验证
10

2.3 交叉验证
图 2.5: K 折交叉验证示意图(K=5)
(leave-one-out cross-validation。LOOCV)。还可以每次取 P 个样本验证。重复 C
P
N
次。这种方
法称为留 P 法(leave-p-out cross-validation。LPOCV)。留一法和留 P 法适用于样本量较小的
情形。当样本量较大时。上述两种方法所需的重复次数较大。运算速度相对较慢。因此通常不采
用留一法和留 P 法。而是使用 K 折交叉验证。
2.3.4 时序交叉验证
以上四种传统交叉验证方法成立的前提是样本服从独立同分布。独立是指样本之间不存在相关
性。从一条样本无法推知另一条样本的取值;同分布是指包括训练集和验证集在内的全部样本需
取自同一分布。当样本是时间序列时。数据随时间演进的过程生成。可能包含周期性、过去和未
来数据间相互关系等信息。并不满足交叉验证中数据独立同分布的基本假设。此时如果依然采
用传统交叉验证方法。可能会将未来时刻的数据划入训练集。历史时刻的数据划入验证集。进而
出现用未来规律预测历史结果的“作弊”行为。因此需要一种既能保证数据利用率。又能保留时
序数据之间相互关系的交叉验证方法。这就是时序交叉验证方法(time-series cross-validation)。
如下图所示。
图 2.6: 5 折时序交叉验证
以上图为例说明时序交叉验证方法。假设样本时间跨度为 10 个月。采用 5 折时序交叉验证。那
么首先将样本等分成 5 个部分。以第 1 2 月数据作为训练集。第 3 4 月作为验证集。进行第 1
次验证。再以第 1 4 月数据作为训练集。第 5 6 月为验证集。进行第 2 次验证。以此类推。第 4
次验证以第 1 8 月数据作为训练集。第 9 10 月作为验证集。再将总共 4 次验证的模型评价指标
取平均数。时序交叉验证避免了使用未来信息的可能。对于时序数据的机器学习而言是较为合
理的选择。
Tashman(2000)、Varma 和 Simon(2006)和 Bergmeir 和 Benitez(2012)等研究表明。时
序交叉验证方法在时序数据上的表现优于传统交叉验证方法。时序特性是金融数据的典型特征。
然而时序交叉验证在投资领域的效果尚没有被系统性地测试。
11
2.3 交叉验证
12

第三章 评估模型
对于一个具体的模型,如何评估其泛化能力呢?模型的泛化能力的评价需要人为制定标准,这就
是性能度量 (performance measure)。
衡量模型泛化能力也就是计算模型的测试误差,性能度量也就是测试误差的具体实例。
性能度量反映了任务需求,在对比不同模型的能力时,使用不同的性能度量往往会导致不同的评
判结果。也就是模型的好坏并不是绝对的,这视不同的性能度量而定,而选取什么样的性能度量
取决于任务需求。
以下介绍常见的性能度量。
在预测任务中,给定样本集 D = {(x
i
, y
i
)} i = 1, 2, ··· , m,其中 y
i
是实例 x
i
的真实 label。要
评估学习器 f 的性能,就要把学习器预测结果 f (x) 与真实 label y 进行比较。
3.1 回归
3.1.1 均方误差
在回归任务中,即预测连续值的问题,最常用的性能度量是“均方误差”(mean squared error)。
E(f ; D) =
1
m
m
X
i=1
(f (x
i
) − y
i
)
2
(3.1)
更一般的,对于数据分布 D 和概率密度函数 p(·),均方误差可描为:
E(f ; D) =
Z
x∼D
(f(x) − y)
2
p(x)dx (3.2)
均方误差在数理统计中说过了,这里再强调一下:均方误差是反映估计量与被估计量之间差异程
度的一种度量。当估计量是无偏时,均方误差就是方差。
3.2 分类
3.2.1 混淆矩阵
对于分类问题来说,很多评价指标都来源于二分类的混淆矩阵,多分类或多标签的评价指标则从
二分类的评价指标拓展得到。
对于二分类问题,分类结果混淆矩阵如表3.1所示:
13

3.2 分类
表 3.1: 混淆矩阵
真实情况
预测结果
正例 反例
正例 TP(真正例) FN(假反例)
反例 FP(假正例) TN(真反例)
对于二分类问题,样本被分为了正类和负类,其预测结果也只有两种:正类或负类,因此可以将
所有样本分为四类:
• True Positive:实际为正类,预测结果也是正类,也称真阳性或者命中 (Hit)。
• True Negative:实际为负类,预测结果也是负类,也称真阴性或者正确拒绝 (Correct Re-
jection)。
• False Positive:实际为负类,预测结果却是正类,也称伪阳性或假警报 (False Alarm),指
代统计学第一型错误 (Type I Error)。
• False Negative:实际为正类,预测结果却是负类,也称伪阴性或未命中 (Miss),指代统计
学第二型错误 (Type II Error)。
进一步,为了更好的理解这种样本分类,我们还可以按照三种不同的方法将这四种类别归为两大
类:
按照预测结果是否正确进行归类:
1. 预测正确的样本:TP + TN
2. 预测错误的样本:FN + FP
按照样本的实际类别进行归类:
1. 实际类别为正类的样本:TP + FN
2. 实际类别为负类的样本:TN + FP
按照样本的预测类别进行归类:
1. 预测为正类的样本:TP + FP
2. 预测为负类的样本:TN + FN
下面介绍的性能度量,用于从不同的侧面对模型进行描述,其共同之处是都是由 TP、TN、FP、
FN 中的部分或全部所组成的表达式。
3.2.2 Error Rate 与 accuracy
在分类任务中,即预测离散值的问题,最常用的是错误率和精度。
定义3.1 Error Rate(错误率): 分类错误的样本数占样本总数的比例。
定义3.2 accuracy(精度,准确率): 分类正确的样本数占样本总数的比例,简记为 ACC。
一般来说,说到 accuracy,指的都是总的准确率,但实际上,不仅可以计算出总分类的 accuracy
和 Error Rate,也可以计算出各分类的 accuracy 和 Error Rate。
以下是总分类情形下的定义:
错误率定义为:
E(f ; D) =
1
m
m
X
i=1
I (f (x
i
) ̸= y
i
) (3.3)
14
3.2 分类
正确率定义为:
acc(f; D) =
1
m
m
X
i=1
I (f (x
i
) = y
i
)
= 1 − E(f ; D)
(3.4)
更一般的,对于数据分布 D 和概率密度函数 p(·) ,错误率与精度可分别描述为:
E(f ; D) =
Z
x∼D
I(f(x) ̸= y)p(x)dx
(3.5)
acc(f; D) =
Z
x∼D
I(f(x) = y)p(x)dx
= 1 − E(f ; D)
(3.6)
以下是各分类情形下的定义:
根据混淆矩阵
(
表3.1),各分类的错误率和准确率定义如下:
E
P
(f; D) =
T N
T P + F N
E
N
(f; D) =
F P
T N + F P
acc
P
(f; D) =
T P
T P + F N
acc
N
(f; D) =
T N
T N + F P
(3.7)
3.2.3 Precision、Recall
错误率和精度虽然常用,但不能满足所有的需求,例如:在推荐系统中,我们只关心推送给用户
的内容用户是否感兴趣(即查准率),或者说所有用户感兴趣的内容我们推送出来了多少(即查
全率)。因此,使用查准/查全率更适合描述这类问题。
定义3.3 Recall(查全率、召回率): 模型挑选出正类样本的能力。所有正例样本中,预测正确
的样本所占比例。
定义3.4 Precision(查准率): 在所有预测为正例的样本中,预测正确的样本所占比例。
P recision =
T P
T P + F P
(3.8)
Recall =
T P
T P + F N
(3.9)
根据上式,可以看出,Recall 就是各分类情形下的 accuracy。
很多时候,分类模型的精度与召回率之间存在着某种此消彼长的关系。通常只有在一些简单的
任务中,才可能使 Recall、Precision 都很高。
对于某些应用来讲,我们可能希望 Precision 越高越好,那么就需要适当牺牲一些召回率,将分
类阈值调高;而对于另一些应用来讲,我们可能希望 Recall 越高越好,那么就需要适当牺牲一
些 Precision,将分类阈值调低,从而使更多的样本被分为正类。因此,对于不同的应用场景,对
Precision 和 Recall 的关注程度也会有所不同,需要根据实际情况进行权衡。
在很多情形下,学习器可以得到样本属于正类的概率(或者其他度量样本属于正类可能性大小
的量)。我们可以按概率的大小对样本进行排序,然后逐个把样本对应的概率作为分类阈值,则
每次可以计算出当前的 Precision 和 Recall。以 Precision 和 Recall 分别作为纵轴、横轴,就得
到了“查准率-查全率曲线”,简称“P-R 曲线(Precision Recall Curve)”,显示该曲线的图称
为”P-R 图”。
P-R 曲线的作用:很好地表示精度与召回率之间的权衡关系,在实际应用中可以根据实际情况
选取曲线上合适的点所对于的分类阈值作为最终分类器的阈值。
示意图中有三个学习器的 P-R 曲线。
15
3.2 分类
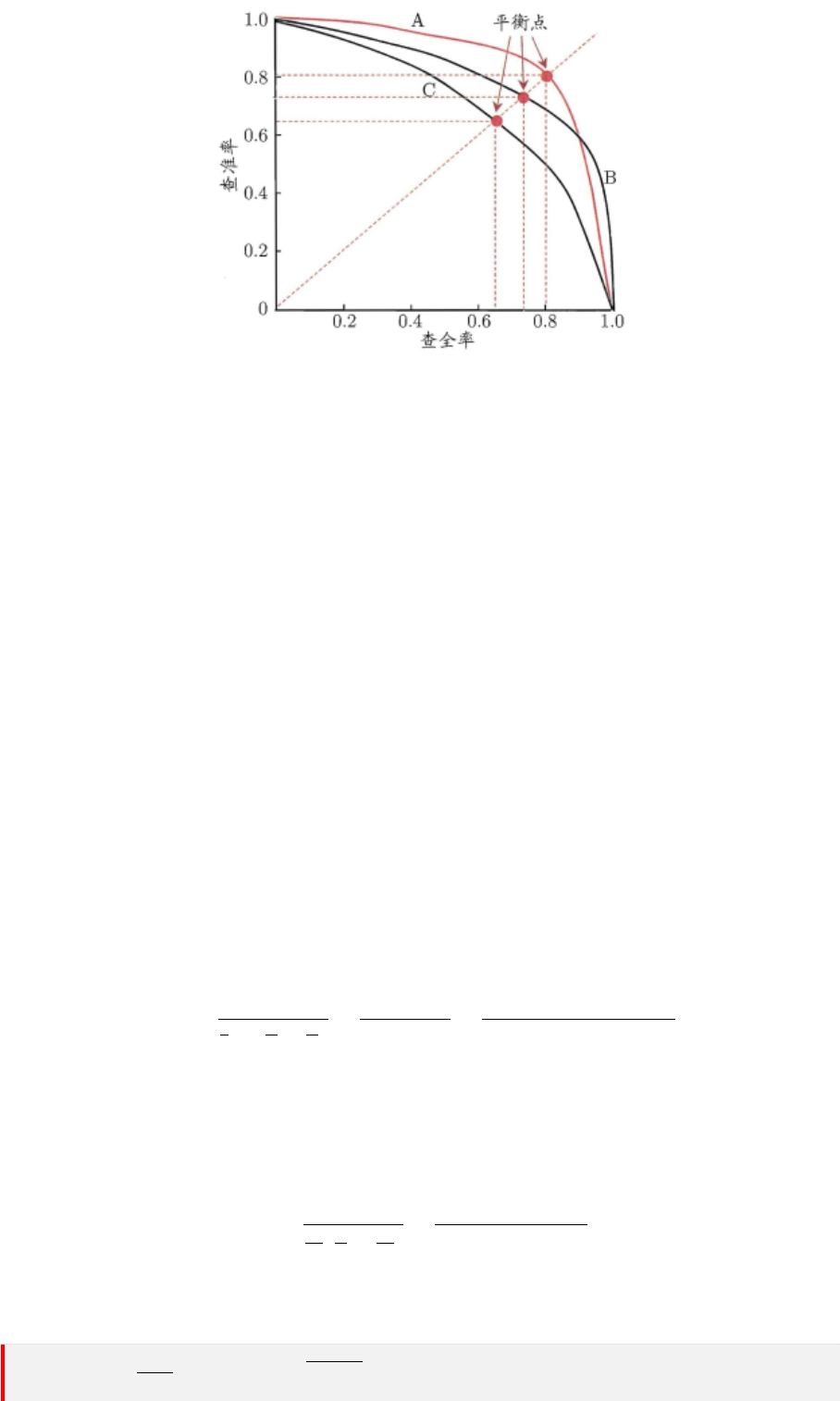
图 3.1: Precision Recall Curve
1. 显然,若一个学习器 C 的 P-R 曲线被另一个学习器 A 的 P-R 曲线完全包住,
则称:A 的性能优于 C。
如果两个学习器的 P-R 曲线发生了交叉,例如图3.1中的 A 与 B ,则不能一般性地断言两者孰
优孰劣。只能在具体的查准率或查全率条件下进行比较。然而,在很多情形下,人们往往仍希望
把学习器 A 与 B 比出个高低。存在以下比较准则:
2. 若 A 和 B 的曲线发生了交叉,则谁的曲线下的面积大,谁的性能更优。
但曲线下的面积难以进行估算,所以,人们设计了一些综合考虑查准率、查全率的性能度量,例
如平衡点(平衡点如图3.1所示)。
3. 平衡点(Break-Event Point,简称 BEP):即当 P=R 时的取值,平衡点的
取值越高,性能更优。
但 BEP 还是过于简化了些,更常用的是 F1 度量 (F1 度量实际是调和平均值):
4. F1 值越大,性能越优。
F 1 =
1
1
2
× (
1
P
+
1
R
)
=
2 × P × R
P + R
=
2 × T P
样本总数 + T P − T N
(3.10)
容易证明:F1 Score 与查准率和召回率之间存在着正向的关系,也就是查准率越高,F1 Score 就
越大,同样召回率越高,F1 Score 也就越大。
但是在一些应用中,对查准率和查全率的重视程度有所不同,这就需要对它们赋予不同的权重,
因此有 F1 的更一般形式 F
β
(加权调和平均):
F
β
=
1
1
β
2
(
1
P
+
β
2
R
)
=
(1 + β
2
) × P × R
β
2
× P + R
(3.11)
其中 β > 0 度量了查全率对查准率的相对重要性。β = 1 时退化为标准的 F1; β > 1 时查全率有
更大影响; β < 1 时查准率有更大影响。
与算术平均
P +R
2
和几何平均
√
P × R 相比,调和平均更重视较小值。
16
3.2 分类
3.2.4 TPR、FPR
定义3.5 TPR: True Positive Rate,真正例率。所有正例样本中,预测正确的样本所占比例。
TPR 就是 Recall。
定义3.6 FPR: False Positive Rate,伪阳性率、假正例率、也称误报率(Probability of False
Alarm)、错误命中率、假警报率,简记为 FPR。在所有实际上为负类的样本中,误判为正类的
样本所占的比例。
T P R =
T P
T P + F N
(3.12)
F P R =
F P
T N + F P
(3.13)
除了 TPR、FPR,还有真负例率和假负例率。TPR、FPR 有一个很好的特性:对数据集是否均
衡不敏感,因为 TPR、FPR 的分子和分母只涉及了单一类别的样本。ROC 曲线以 TPR、FPR
基础的,所以这也是 ROC 曲线的优点。
3.2.5 ROC、AUC
很多学习器是为测试样本产生一个实值或概率预测,然后将这个预测值与一个分类阈值 (thresh-
old) 进行比较,若大于阈值则分为正类,否则为反类。这个实值或概率预测结果的好坏,直接
决定了学习器的泛化能力。实际上,根据这个实值或概率预测结果,我们可将测试样本进行排
序,“最可能”是正例的排在最前面,” 最不可能” 是正例的排在最后面。这样,分类过程就相当
于在这个排序中以某个” 截断点” (cut point) 将样本分为两部分,前一部分判作正例,后一部分
则判作反例。
定义3.7 ROC:ROC 曲线的全称为 Receiver Operating Characteristic,其纵轴为 True Positive
Rate (TPR),也就是召回率,横轴为伪阳性率 False Positive Rate (FPR)。显示 ROC 曲线的图
称为”ROC 图。
下图给出了一个示意图:
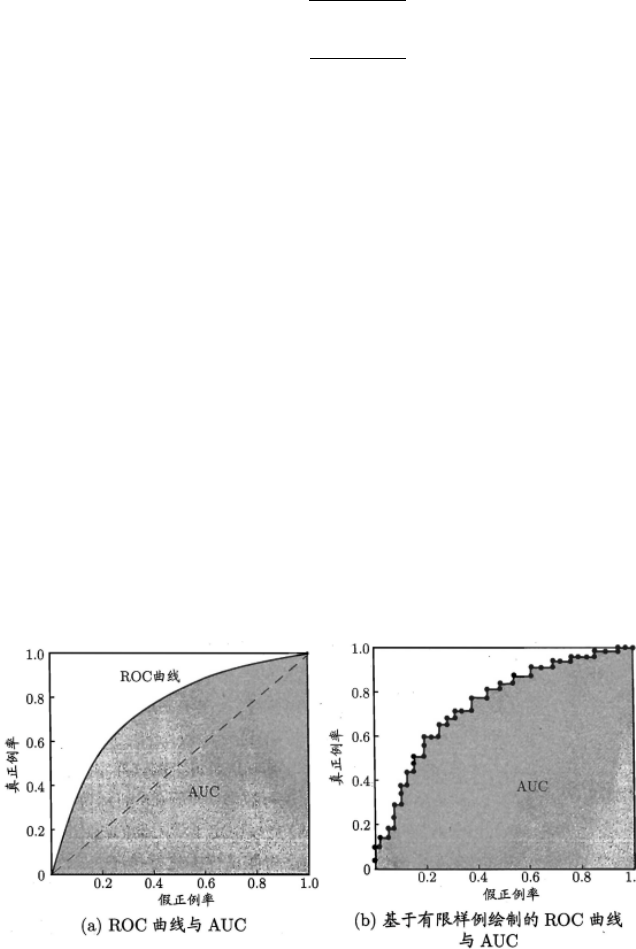
图 3.2: roc 与 auc 曲线
看几个特殊点或特殊曲线:
• 第一个点:(0, 1),F P R = 0 T P R = 1 ,这意味着所有的样本都分类正确。
• 第二个点:(1, 0),F P R = 1T P R = 0 ,和第一个点比较,这是第一个点的完全反面,意
味着是个最糟糕的分类器,将所有的样本都分类错误了(但其实可以直接取反,就是最好
的模型,因为是二分类问题)。
• 第三个点:(0, 0),F P R = 0T P R = 0 也就是原点,这个点表示的意思是,分类器预测所
有的样本都为负类。
17
3.2 分类
• 第四个点:(1, 1),F P R = 1T P R = 1,和第三个点对应,表示分类器预测所有的样本都为
正类。
• 一条线:y = x,对角线对应于“随机猜测”模型。
于是,对于特定的分类模型,如果 ROC 曲线位于对角线左上方,说明模型性能好于随机猜测,
如果 ROC 曲线位于对角线右下方,说明模型性能劣于随机猜测。
图3.2(a) 是理想化的 ROC 曲线图,但在现实任务中,通常只能利用有限个测试样本来绘制 ROC
图,此时只有有限个 (T P R, F P R) 坐标对,无法产生图3.2(a) 中的光滑 ROC 曲线,只能绘制
出图3.2(b) 中的近似 ROC 曲线。绘制 ROC 曲线的过程如下:
设数据集共有 m
+
个正例,m
−
个反例
1. 将所有的样本按模型的预测打分 (score) 由大到小排序;
2. 将分类阈值设为最大,即把所有样本都归类为反例,此时 T P R = F P R = 0,得到 (0, 0)
坐标点;
3. 将分类阈值依次设为每个样本的打分,即依次把每个样本划分为正例。设前一个标记点的
坐标为 (x, y),若当前为真正例,则当前标记点的坐标为 (x, y +
1
m
+
),若当前为假正例,则
当前标记点的坐标为 (x +
1
m
−
, y)。
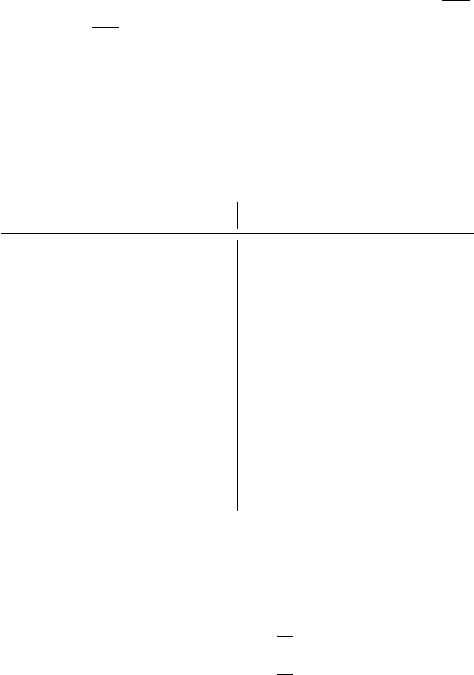
现设数据集共有 10 个正例,10 个反例,如下表。Class 一栏表示每个测试样本真正的标签(p
表示正样本,n 表示负样本),Score 表示每个测试样本属于正样本的概率。我们根据每个测试样
本属于正样本的概率值从大到小排序。
num Class Score num Class Score
1 p 0.9 11 p 0.4
2 p 0.8 12 n 0.39
3 n 0.7 13 p 0.38
4 p 0.6 14 n 0.37
5 p 0.55 15 n 0.36
6 p 0.54 16 n 0.35
7 n 0.53 17 p 0.34
8 n 0.52 18 n 0.33
9 p 0.51 19 p 0.3
10 n 0.505 20 n 0.1
1. 阈值 t > 0.9,则 T P = F P = 0,T P R = 0,F P R = 0;
2. 阈值 t ≥ 0.9,则 T P = 1,F P = 0,T P R =
1
10
,F P R = 0;
3. 阈值 t ≥ 0.9,则 T P = 1,F P = 0,T P R =
1
10
,F P R = 0;
4. ···
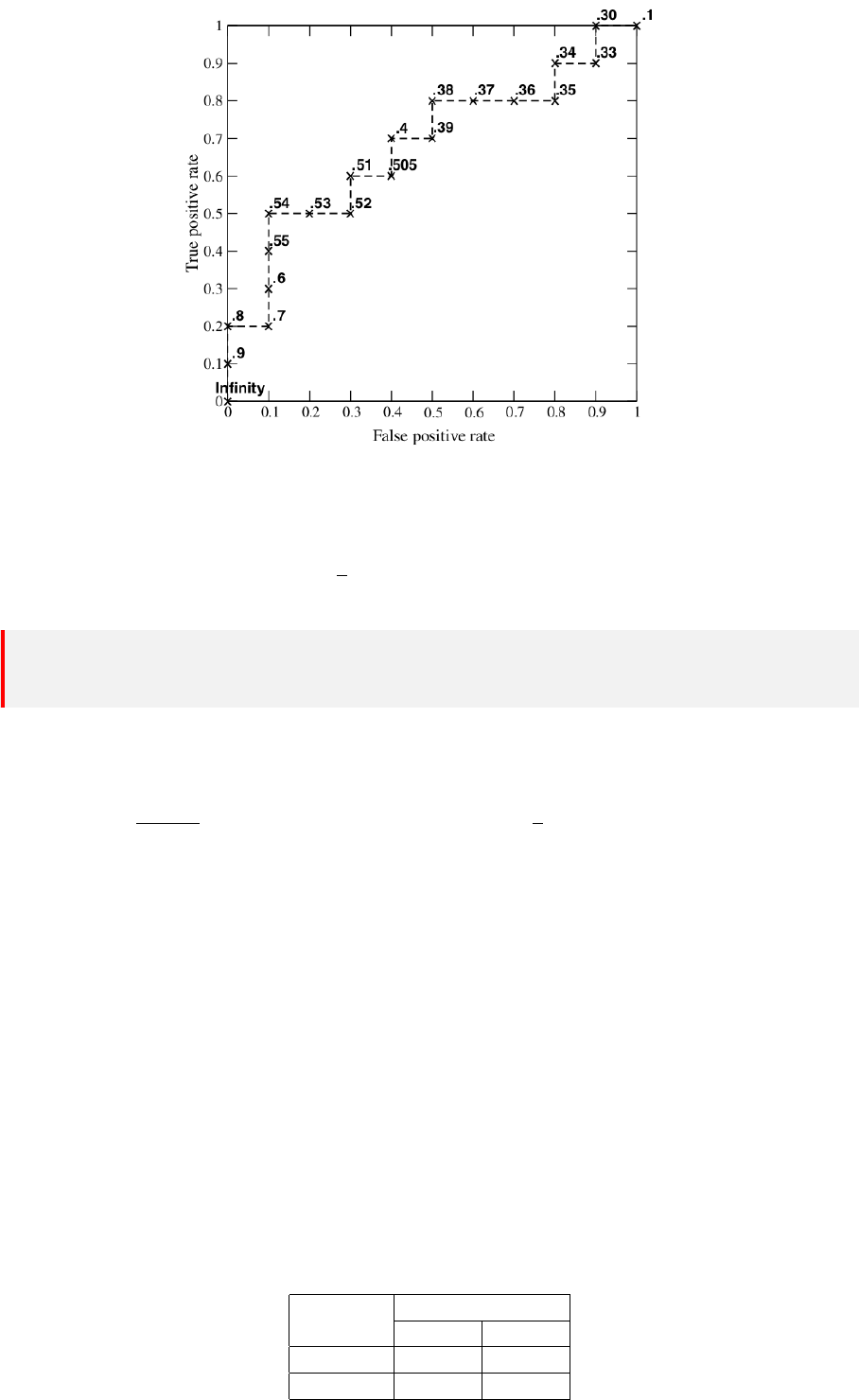
5. 阈值 t ≥ 0.1,则 T P = 10,F P = 10,T P R = 1,F P R = 1。
最后绘制出来的 ROC 图如下所示:
ROC 曲线可以很直观的展示模型的好坏,但是如果不同模型的 ROC 曲线存在交叉,则很难依
靠视觉来对模型的优劣进行比较,此时可以使用曲线下面积 (Area Under Curve, AUC) 这个指
标来进行评价。
定义3.8 AUC: 指的是 ROC 曲线右下方的面积,该面积越大,一般表示模型的预测能力越好,
此时可以将 ROC 曲线上离左上角最近的点所对于的分类阈值作为最终分类器的阈值。
由定义可知,AUC 可通过对 ROC 曲线下各部分的面积求和而得。假定 ROC 曲线是由坐标为
{(x
1
, y
1
), (x
2
, y
2
), ··· , (x
m
, y
m
)} 的点按序连接而形成 (x
1
= 0, x
m
= 1),参见图3.2(b),则 AUC
18
3.2 分类
可估算为:
AUC =
1
2
m−1
X
i=1
(x
i+1
− x
i
) · (y
i
+ y
i+1
) (3.14)
这是梯形面积的计算公式,因为当存在正例和反例的打分相等时,则会出现梯形;若不存
在这种情况,则只会出现长方形,而长方形的面积亦可使用梯形面积公式计算。
形式化地看,AUC 考虑的是样本预测的排序质量,因此它与排序误差有紧密联系,给定 m
+
个
正例和 m
−
个反例,另 D
+
和 D
−
分别表示正、反例集合,则排序“损失”(loss) 定义为
ℓ
rank
=
1
m
+
m
−
X
x
+
∈D
+
x
−
p
−
I
f
x
+
< f
x
−
+
1
2
I
f
x
+
= f
x
−
(3.15)
即考虑每一对正、反例,若正例的预测值小于反例,则记一个罚分,若相等,记 0.5 个罚分。容
易看出,ℓ
rank
对应的是 ROC 曲线之上的面积:若一个正例在 ROC 曲线上对应标记点的坐标为
(x, y),则 x 恰是排序在其之前的反例所占的比例,即假正率。因此有
AUC = 1 − ℓ
rank
(3.16)
3.2.6 代价敏感错误率
有时候,不同类型的错误所造成的后果不同。为权衡不同类型错误所造成的不同损失,可为错误
赋予“非均等代价”(unequa1 cost)。
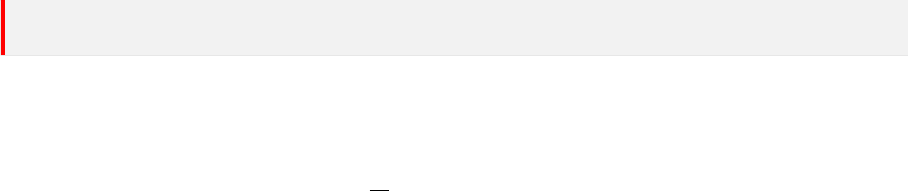
以二分类任务为例,我们可以根据任务的领域知识设定一个“代价矩阵”(cost matrix),如下表
所示。其中,cost
ij
表示将第 i 类样本预测为第 j 类样本的代价。一般来说,cost
ii
= 0。
真实情况
预测结果
第 0 类 第 1 类
第 0 类 0 cost
01
第 1 类 cost
10
0
19
3.2 分类
重要的是代价比值而非绝对值,例如 cost
01
: cost
01
= 5 : 1 与 50 : 10 的效果是一样的。
前面介绍的性能度量都是假设均等代价,也就是犯错误次数越少越好。在非均等错误代价下,我
们希望的是最小化“总体代价”,则“代价敏感”错误率为:
E(f ; D; cos t) =
1
m
X
x
i
∈D
+
I (f (x
i
) ̸= y
i
) × cos t
01
+
X
x
i
∈D
−
I (f (x
i
) ̸= y
i
) × cos t
10
(3.17)
其中,第 0 类作为正类、第 1 类作为反类,D
+
与 D
−
分别代表样本集 D 的正例集和反例集。
20
第四章 信息熵 *
21
22
第二部分
机器学习中阶
传统模型
23
第五章 决策树
5.1 简介
决策树起源于概念学习系统 CLS (concept learning system)。CLS 最早由 Hunt.E.B 等人于 1966
年提出,并首次用决策树进行概念学习,后来的许多决策树学习算法都可以看作是 CLS 算法的
改进与更新。CLS 的主要思想是从一个空的决策树出发,通过添加新的判定节点来完善原有的
决策树,直到新的决策树能够正确地将训练实例分类为止。
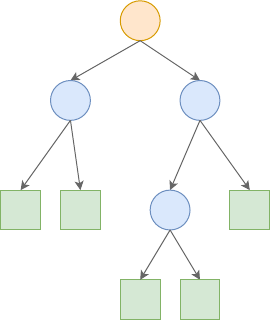
决策树由结点(node)和有向边(directed edge)组成。结点有两种类型:
• 内部结点(internal node):表示一个特征或属性。内部结点又可以分为父结点(parent
node)和子结点(child node),这是一种相对关系。
• 叶结点(leaf node, terminal node):表示一个类。
树的第一个结点往往会被称为根节点。
图 5.1: 决策树简图
图中圆型表示内部结点,方形表示叶结点。
25

5.2 决策树基本算法
5.2 决策树基本算法
现在已经有很多种决策树算法,但是大多数决策树算法都是以下核心算法的变体。
Algorithm 1: Decision Tree
Input: 训练集 D = {(x
1
, y
1
) , (x
2
, y
2
) , . . . , (x
m
, y
m
)};
属性集 A = {a
1
, a
2
, . . . , a
d
}.
1 Function TreeGenerate(D, A)
2 begin
3 生成结点 node;
4 if D 中样本全属于同一类别 C then
5 将 node 标记为 C 类叶节点; return
6 end
7 if A = ∅ or D 中样本在 A 上取值相同 then
8 将 node 标记为叶结点, 其类别标记为 D 中样本权重之和最大的类; return
9 end
// 决策树算法的关键
10 从 A 中选择最优划分属性 a
∗
11 for a
∗
的每一个值 a
v
∗
do
12 为 node 生成一个分支;
13 令 D
v
表示 D 中在 a
∗
上取值为 a
v
∗
的样本子集;
14 if D
v
为空 then
// 如果 a
v
∗
的样本全都被分到其他结点, D
v
则会为空
// 即使训练集不存在进入该结点的样本, 但预测时可能有新样本进入该节点
15 将分支结点标记为叶结点, 其类别标记为 D 中样本权重之和最大的类; return
16 else
17 以 TreeGenerate (D
v
, A\{a
∗
}) 为分支结点
18 end
19 end
20 end
Output: 以 node 为根节点的一颗决策树
决策树的生成可以使用上述递归算法。在决策树基本算法中,有三种情形会致递归的返回:
1. 当前结点包含的样本全属于同一类别,无需划分
2. 当前性集为空,或是所有样本在所有属性上取值相同,无法划分
3. 当前结点包含的样本集合为空,不能划分
情形 2 和情形 3 的处理方式类似,但情形 2 是在利用当前结点的后验分布,而情形 3 则是把父
结点的样本分布作为当前结点的先验分布。
5.3 划分选择
直觉上,随着划分过程不断进行,我们希望决策树的分支结点所包含的样本尽可能属于同一类
别,即结点的“纯度”(purity)越来越高。更具体来说:
1. 如果结点的类别数量不变,我们希望某个类别所占比例越高越好;
2. 如果结点的类别数量发生变化,我们希望结点的类别数量越少越好。
也就是说,我们想找到一个量去量化“纯度”,在样本类别个数不变的条件下,这个量应该随着
类别所占比例的增加而单调递增;如果样本类别个数发生变化,这个量应该随着类别个数的增加
而单调递减。另外,为了方便数学上的处理,我们可能还希望这个量永远不会取到负值,如果是
连续的就更好了。
实际上,以上两点都可以归结为一点,即属于某个类别的样本数量占整个结点的样本总数的比
例越高越好。因为结点类别数量减少,即是某些类别的样本所占比例为 0。同时,基于大数定律,
26

5.3 划分选择
当样本量较大时,比例可以作为概率的近似。因此,purity 应该是一个关于各个类别概率的函数,
该概率分布越集中,purity 的值越大。
如果有一个量,当类别概率分布越集中时,这个量的取值越小,那么它也可以作为 purity 的度
量,只需要将其取倒数即可。这样的量被称为 impurity。显然,在数学上,purity 和 impurity
都是一样的,它们可以相互转换。实际应用时,一般使用 impurity。
我们可以将上面的描述,转换为 impurity 函数的数学定义。
定义5.1 impurity function: impurity 函数 Φ 是定义在 k 维数组 (p
1
, ··· , p
k
) 上的函数,并
具有以下三条性质:
1. Φ 在 p
j
是均匀分布(即所有 p
j
相等)时达到最大值。
2. Φ 只有在 p
j
= 1, j ∈ (1, 2, ··· , k) 时达到最小值。
3. Φ 是一个对称函数,即置换各个 p
j
的位置,Φ 的值不变。
其中,p
j
满足 p
j
≥ 0, j ∈ (1, 2, ··· , k), Σ
j
p
j
= 1。
purity 函数可以有不同的定义,但是它们都满足这个三条性质。
定义5.2 impurity measure: 给定一个 impurity 函数 Φ,则一个结点 t 的 impurity 为:
i(t) = Φ(p(1 | t), p(2 | t), . . . , p(k | t))
其中 p(j | t) 是给定结点 t 中的类 j 的估计条件概率(经验后验概率)。
根据 impurity measure 可以定义结点 t 的分裂优度。
定义5.3 goodness of split s for node t: 假设决策树是一颗二叉树,那么分裂优度记为
Φ(s, t)。
Φ(s, t) = ∆i(s, t) = i(t) − p
L
i(t
L
) − p
R
i(t
R
)
其中,权重 p
L
和 p
R
分别是 t 结点的样本进入左右子结点的比例。
Φ(s, t) 值最大的属性为最优划分属性。
树 T 的 impurity measure 总和为
I(T ) =
X
t∈
˜
T
I(t) =
X
t∈
˜
T
i(t)p(t)
˜
T 是 T 树所有的叶子结点,p(t) 是样本进入 t 结点的概率。
5.3.1 信息增益
使用信息熵 E
1
衡量某个结点的“纯度”,使用加权的信息熵衡 E
2
量该结点的所有子节点的“纯
度”。我们显然希望,该结点通过该次分裂,“纯度”尽可能的提高。也就是说 E
1
− E
2
的值越
大越好。于是 E
1
和 E
2
的差就可以用于选择最优“划分属性”。
E
1
和 E
2
的差被称为信息增益(Information Gain)。选择划分属性时,计算出样本每个属性对
应的 Gain,再选择最大的 Gain 对应的属性作为划分属性即可。
定义5.4 信息熵: 假定当前样本集合 D 中第 k 类样本所占的比例为 p
k
(k = 1, 2, . . . , |Y|),则
D 的信息熵定义为
Ent(D) = −
|Y|
X
k=1
p
k
log
2
p
k
(5.1)
27
5.3 划分选择
实际上,在信息熵的定义中,p
k
代表概率,但基于大数定律,样本量较大时,可以用频率
(比例)近似概率。
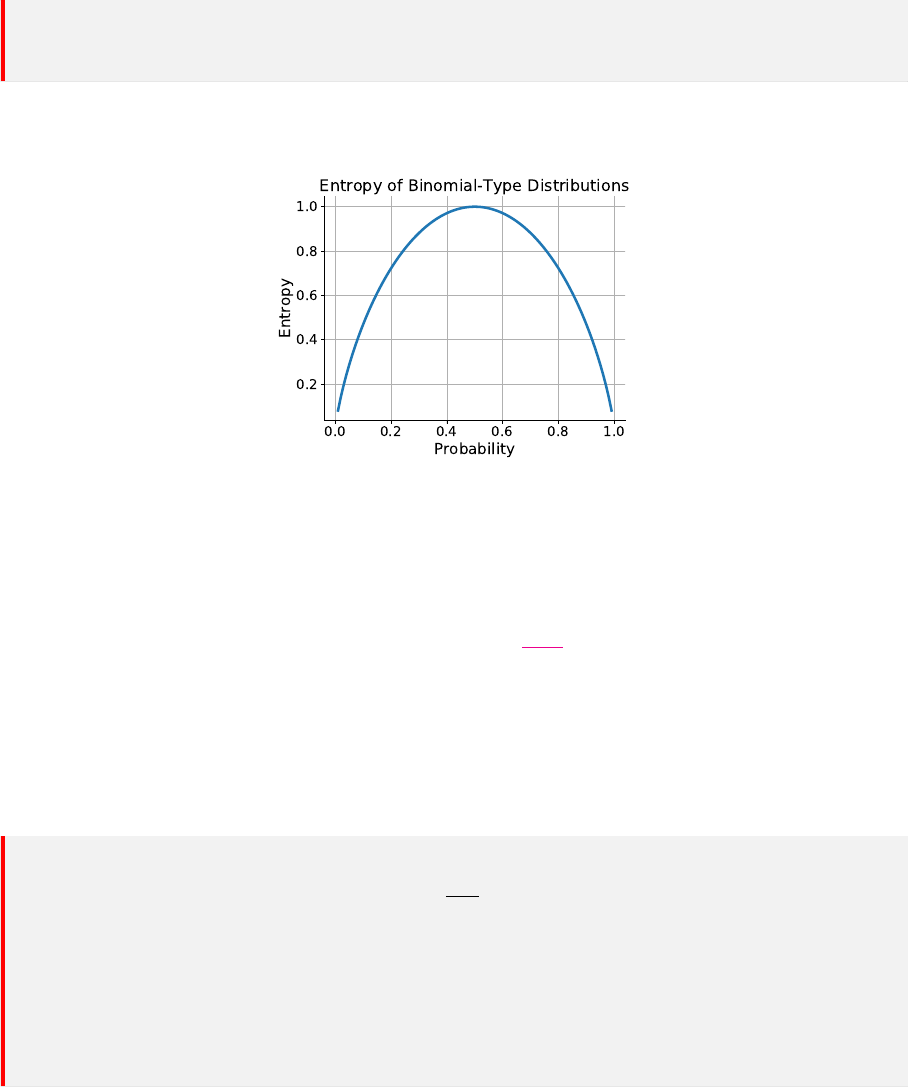
可以观察当样本类别为二分类时,信息熵的大小与某个类别的样本所占比例的关系。
定义5.5 信息增益: 假定离散属性 a 有 V 个可能的取值
a
1
, a
2
, . . . , a
V
, 若使用 a 来对样本
集 D 进行划分,则会产生 V 个分支结点, 其中第 v 个分支结点包含了 D 中所有在属性 a 上取
值为 a
v
的样本, 记为 D
v
。
Gain
(
D, a
) =
Ent
(
D
)
−
V
X
v=1
|D
v
|
|D|
Ent
(
D
v
)
(5.2)
注意到公式5.2标红显示的部分,|D
v
|/|D| 是各个分支结点的权重,因此样本数越多的分支结点
的影响越大。
最终选择属性 a
∗
= arg max
a∈A
Gain(D, a)。
实际上,在 Gain(D, a) 的公式中,Ent(D) 对于当前结点来说是定值,且 Gain(D, a) 为非
负数,所以选择最优属性只需要选择
P
V
v=1
|D
v
|
|D|
Ent (D
v
) 值最小的属性即可。
大多数资料直接说选择 Gain(D, a) 值最大的属性作为划分属性,这可能有以下三点原因:
1. 为了统一各个 impurity measure 分裂优度公式的形式。
2. 为了从 Gain 引出 Gain ratio 的定义。
3. 预剪枝策略需要用到 Gain 值。
ID3 决策树学习算法 [Quinlan, 1986] 就是以信息增益为准则来选择划分属性,但信息增益准则
有一个缺点——偏好可取值数目较多的属性。
注意到,信息熵的计算公式5.1中需要计算各类样本的概率,这个概率是用频率去估计的。根据
大数定律,只有当样本数足够多的时候,频率才可以足够精确地近似概率。假设选择可取值数目
为 k 的属性进行划分,即需要为 k 个子结点估计类别分布,k 越大,需要估计的次数越多,而
每个子结点的样本数又越小,频率的方差越大。方差越大,即说明将类别的概率分布估计得比真
实分布更为集中的概率越大。类别分布更集中导致子结点的熵越小,即信息增益越大。
5.3.2 信息增益比
因为信息增益准则对可取值数目较多的属性有所偏好,为减少这种偏好可能带来的不利影响,著
名的 C4.5 决策树算法 [Quinlan,1993] 不直接使用信息增益,而是使用“信息增益比”(information
gain ratio)来选择最优划分属性。
28

5.4 连续值处理
定义5.6 增益率:
Gain
−
ratio(D, a) =
Gain(D, a)
IV(a)
(5.3)
其中
IV(a) = −
V
X
v=1
|
D
v
|
|D|
log
2
|
D
v
|
|D|
(5.4)
IV 称为属性 a 的“固有值”(intrinsic value) [Quinlan, 1993]。
增益率实际上是将子分支结点的加权信息熵作为子分支结点的惩罚项 IV。属性 a 的可能取值数
目越多 (即子分支的数量 V 越大),则 IV(a) 的值通常会越大。
显然,增益率准则对可取值数目较少的属性有所偏好,因此,C4.5 算法 [Quinlan, 1993] 并不是
直接选择增益率最大的候选划分属性,而是使用了一个启发式:先从候选划分属性中找出信息增
益高于平均水平的属性,再从中选择增益率最高的。
5.3.3 基尼指数
与 ID3、C4.5 不同,CART 决策树 [Breiman et al., 1984] 不使用基于信息熵的量作为选择划分
属性的准则,而是使用“基尼指数”(Gini index)。
定义5.7 基尼指数:
Gini(D) =
|Y|
X
k=1
X
k
′
̸=k
p
k
p
k
′
= 1 −
|Y|
X
k=1
p
2
k
(5.5)
Gini(D) 反映了从数据集 D 中随机抽取两个样本,其类别标记不一致的概率。因此,基尼指数
也是符合我们对描述“纯度”的量的要求的,Gini(D) 越小,则数据集 D 的纯度越高。
属性 a 的基尼指数定义为
Gini index (D, a) =
V
X
v=1
|D
v
|
|D|
Gini (D
v
)
于是, 我们在候选属性集合 A 中,选择那个使得划分后基尼指数最小的属性作为最优划分属性,
即 a
∗
= arg min
a∈A
Gini index(D, a)。
5.4 连续值处理
到目前为止我们仅讨论了基于离散属性来生成决策树。如果决策树遇到连续特征,应该怎么处
理呢?一般来说,我们喜欢将复杂的问题转换为简单的问题,这样就可以将处理简单问题的方法
应用到复杂问题上。
即使连续属性的可取值数目是无穷的,但我们希望通过连续属性离散化的技术,基于现有样本,
将连续属性的无穷取值离散化为有限个取值。
最简单的策略是采用二分法 (bi-partition) 对连续属性进行处理,这正是 C4.5 决策树算法中
采用的机制 [Quinlan, 1993]。
给定样本集 D 和连续属性 a, 假定 a 在 D 上出现了 n 个不同的取值,将这些值从小到大进行排
序,记为
a
1
, a
2
, . . . , a
n
。基于划分点 t 可将 D 分为子集 D
−
t
和 D
+
t
, 其中 D
−
t
包含那些在属
性 a 上取值不大于 t 的样本, 而 D
+
t
则包含那些在属性 a 上取值大于 t 的样本。显然,对相邻
的属性取值 a
i
与 a
i+1
来说,t 在区间
a
i
, a
i+1
中取任意值所产生的划分结果相同。因此,对
连续属性 a,我们可考察包含 n − 1 个元素的候选划分点集合
29

5.5 缺失值处理
T
a
=
a
i
+ a
i+1
2
| 1 ⩽ i ⩽ n − 1
即把区间
a
i
, a
i+1
的中位点
a
i
+a
i+1
2
作为候选划分点。然后,我们就可像离散属性值一样来考
察这些划分点,选取最优的划分点进行样本集合的划分。例如对 Gain 的公式稍加改造:
Gain(D, a) = max
t∈T
a
Gain(D, a, t)
= max
t∈T
a
Ent(D) −
X
λ∈{−,+}
D
λ
t
|D|
Ent
D
λ
t
其中 Gain(D, a, t) 是样本集 D 基于划分点 t 二分后的信息增益。于是,我们就可选择使 Gain(D, a, t)
最大化的划分点。
5.5 缺失值处理
工业界的训练集往往是存在不少缺失值的,决策树算法遇到有缺失值的样本,需要解决两个问
题:
1. 如何在属性值缺失的情况下进行划分属性选择?
2. 给定划分属性, 若样本在该属性上的值缺失, 如何对样本进行划分?
显然,即使训练集存在缺失值,算法也不应该偏好存在缺失值的样本。因为缺失值越多,对模型
性能的负面影响越大。既然这样,训练过程中就应该尽量使用不存在缺失值的样本。因此,C4.5
决策树算法从整个训练集中挑选出不存在缺失值的子集,训练时用该子集替代整个训练集,而该
子集占训练集的比例大小可以作为一种优劣评判准则。
给定训练集 D 和属性 a, 令
˜
D 表示 D 中在属性 a 上没有缺失值的样本子集。对问题 (1),显然
我们仅可根据
˜
D 来判断属性 a 的优劣。假定属性 a 有 V 个可取值
a
1
, a
2
, . . . , a
V
,令
˜
D
v
表
示
˜
D 中在属性 a 上取值为 a
v
的样本子集,
˜
D
k
表示
˜
D 中属于第 k 类 (k = 1, 2, . . . , |Y|) 的样
本子集,则显然有
˜
D =
S
|Y|
k=1
˜
D
k
,
˜
D =
S
V
v=1
˜
D
v
。假定我们为每个样本 x 赋予一个权重 w
x
,并
定义
ρ =
∑
x∈
˜
D
w
x
∑
x∈D
w
x
(5.6)
˜p
k
=
∑
x∈
˜
D
k
w
x
∑
x∈
˜
D
w
x
(1 ⩽ k ⩽ |Y|) (5.7)
˜r
v
=
∑
x∈
˜
D
v
w
x
∑
x∈
˜
D
w
x
(1 ⩽ v ⩽ V ) (5.8)
直观地看,对属性 a,ρ 表示无缺失值样本所占的比例,˜p
k
表示无缺失值样本中第 k 类所占
的比例,˜r
v
则表示无缺失值样本中在属性 a 上取值 a
v
的样本所占的比例。显然,
P
|D|
k=1
˜p
k
=
1,
P
V
v=1
˜r
v
= 1。
基于上述定义, 我们可将信息增益的计算式5.2推广为
Gain(D, a) = ρ × Gain(
˜
D, a)
= ρ ×
Ent(
˜
D) −
V
X
v=1
˜r
v
Ent
˜
D
v
!
(5.9)
其中
Ent(
˜
D) = −
|Y|
X
k=1
˜p
k
log
2
˜p
k
30
5.6 剪枝
对问题 (2),若样本 x 在划分属性 a 上的取值己知,则将 x 划入与其取值对应的子结点, 且样本
权值在子结点中保持为 w
x
。若样本 x 在划分属性 a 上的取值未知,则将 x 同时划入所有子结
点,且样本权值在与属性值 a
v
对应的子结点中调整为 ˜r
v
· w
x
。直观地看, 这就是让同一个样本
以不同的概率划入到不同的子结点中去。
与 C4.5 决策树不同,CART 决策树使用 surrogate splits(替代划分)的方式处理缺失值。CART
会为最佳划分属性计算代替属性,如果样本在最佳划分属性上缺失值,那么将使用替代属性对样
本进行划分。如果样本在最佳替代属性上仍缺失值,则使用次佳替代属性,以此类推。寻找替代
属性的原则是使结点划分的效果与最佳划分属性相似,即划分的误差最小。
另一方面,我们也可以使用这种方式去填充缺失值。
因为 CART 树每一个内部结点都要储存多个划分属性,所以 CART 算法的空间复杂度比 C4.5
大很多。
5.6 剪枝
当一个决策树已经可以把训练样本分类得最准确时,这往往意味着决策树生成的分支过多。如
果预测数据的分布和训练的分布稍微有点不一致,则模型会存在过拟合。通过主动裁掉一些内
部结点,并将其作为新的叶结点,可以降低决策树模型过拟合的风险,这称为剪枝(pruning)。
决策树的剪枝策略可以分为“预剪枝”(pre-pruning) 和“后剪枝”(post-pruning)。
1. 预剪枝:在决策树生成过程中,每生成一个内部结点,便对该内部结点应用剪枝策略。
2. 后剪枝:生成一颗完整的决策树之后,再自底向上地对内部结点应用剪枝策略。
5.6.1 预剪枝
有如下预剪枝策略:
1. 树到达一定深度
2. 结点下包含的样本点小于一定数目
3. impurity(如信息增益、信息增益比等)小于一定的阈值
4. 生成结点后,决策树的性能没有提高,或者代价函数没有下降
5.6.2 后剪枝
因为在后剪枝时,已经生成了一颗完整的决策树,所以通过判断性能或代价函数是否有改善进行
剪枝。
下面介绍几种(后)剪枝策略,实际上,这些预剪枝也可以使用这些剪枝策略,因为预剪枝时,
显然也是可以计算性能评估得分或代价函数的。
5.6.2.1 错误率降低剪枝 (Reduced-Error Pruning, REP)
先从训练集生成一棵完整的决策树,然后自底向上地对非叶结点进行考察,若将该结点对应的子
树替换为叶结点能带来决策树泛化性能提升(或泛化性能不下降),则将该子树替换为叶结点。
REP 策略要求将训练数据划分为两份:训练集和验证集。训练集用于生成决策树,验证集用于
剪枝时评估泛化性能。
31

5.6 剪枝
因为是对泛化性能进行评估,所以训练数据需要被划分为两部分:训练集和验证集。
西瓜书在决策树章节中,介绍的剪枝就是用这种剪枝方法。这个方法的原理是:即使决策树可能
会被训练集中的随机错误和巧合规律所误导,但验证集合不太可能表现出同样的随机波动,所以
验证集可以用来纠正决策树。
REP 剪枝比较简单,不过如果训练数据较少,REP 策略可能会使决策树偏向于过度修剪。
5.6.2.2 悲观错误剪枝 (Pessimistic Error Pruning, PEP)
PEP 剪枝算法是在 C4.5 决策树算法中提出的,该方法直接使用训练数据进行误差评估,不需要
一个单独的测试数据集。
如果直接根据训练集计算错误率,显然完整的树的错误率是最小的,因此需要在错误率计算公式
中添加惩罚因子。
对于一个叶子结点 t,其样本总数为 N
t
,分类错误的样本总数为 E
t
,定义其错误率为
r(t) =
E
t
N
t
修正错误率为(0.5 为修正因子)
r
′
(t) =
E
t
+ 0.5
N
t
˜
T 是树 T 的所有叶子结点,|
˜
T | 是树 T 的叶子结点总数,树 T 的修正错误率为
R
′
(T ) =
P
t∈
˜
T
(E
t
+ 0.5)
P
t∈
˜
T
N
t
=
P
t∈
˜
T
E
t
+ 0.5 |
˜
T |
P
t∈
˜
T
N
t
之所以叫“悲观”,可能是因为每个叶子结点都会主动加入一个惩罚因子,“悲观”地提高错误
率。
当子树 T
t
的误判数大于 t 结点替换为叶结点时的误判数一个标准差,便决定剪枝,得到 T −T
t
。
E
T
t
− Var
T
t
> E
t
其中,Var
T
t
=
p
N
T
t
× R
′
(T
t
) × (1 − R
′
(T
t
))
子树 T
t
每次分类一个样本有两种结果,分类正确(记为 0),分类错误(记为 1),子树 T
t
错误
分类某个样本的概率为 R
′
(T
t
)。因此,每次对样本进行分类可以看作是一次伯努利试验,对 N
T
t
个样本进行分类,则是做了 N
T
t
次独立的伯努利试验,这服从 B(N
t
, R
′
(T
t
)) 二项分布。根据二
项分布的标准差公式,可以计算出 Var
T
t
。
5.6.2.3 代价复杂度剪枝 (Cost-Complexity Pruning, CCP)
CCP 剪枝通过极小化决策树的 cost-complexity measure 实现,这是 CART 决策树所使用的剪
枝算法。
定义5.8 cost-complexity measure: 由 cost function 和 complexity 组成,公式如下:
C
α
(T ) = C(T ) + α|
˜
T |
其中,C(T ) 为代价函数,|
˜
T | 为复杂度(树 T 的叶子结点数量),α 为非负实数,称为复杂度参
数 (complexity parameter)。
代价函数有多种不同的定义,可以选择信息熵、信息增益、信息增益率、基尼系数、平方误差、
32

5.6 剪枝
误分类概率等。
这里介绍两种:
1. 信息熵(《统计学习方法》)
2. 误分类概率
信息熵
设树 T 的所有叶子结点为
˜
T ,所有叶子结点个数为 |
˜
T |,叶结点 t 有 N
t
个样本点,其中 k 类的
样本点有 N
k
个, k = 1, 2, ··· , K,H
t
(T ) 为叶结点 t 上的经验熵
H
t
(T ) = −
X
k
N
k
N
t
log
N
ik
N
t
树 T 的代价函数为
C(T ) =
|
˜
T |
X
t=1
N
t
H
t
(T ) = −
|
˜
T |
X
t=1
K
X
k=1
N
tk
log
N
tk
N
t
误分类概率
将误分类概率作为代价函数:
C(T ) =
X
t∈
˜
T
r(t) · p(t) =
X
t∈
˜
T
C(t)
其中
r(t) = 1 − max
j
p(j | t) = 1 − p(κ(t) | t)
κ(t) = arg max
j
p(j | t)
p(j | t) =
N
j
(t)
N(t)
其中,j 代表样本类别,N
j
(t) 为叶子结点 t 中属于类 j 的样本总数,r(t) 为叶子结点 t 的误分
类概率的再代入估计(
resubstitution estimate
)。
剪枝过程
对于固定的 α, 一定存在使损失函数 C
α
(T ) 最小的子树,将其表示为 T
α
,
C
α
(T (α)) = min
T ≤T
nax
C
α
(T )
显然,最优子树 T
α
是存在的,因为树 T 的子树只有有限个。容易验证这样的最优子树是唯一
的。
较大的 α 促使选择较小的树;而较小的 α 促使选择较大的树。极端情况,当 a = 0 时,整体树
是最优的,而当 a → ∞ 时,单结点树是最优的。
Breiman 等人证明:可以用递归的方法对树进行剪枝。将 α 从小增大,如 0 = α
1
< α
2
< . . . <
α
n
< +∞,将产生一系列的区间 [α
i
, α
i+1
) , i = 1, 2, . . . , n。剪枝得到的最优子树序列与区间
[α
i
, α
i+1
) 一一对应。{T
1
, T
2
, . . . , T
n
} 序列中的子树是嵌套的,即 T
1
⊃ T
2
⊃ . . . ⊃ T
k
⊃ . . . ⊃ T
n
。
33
5.6 剪枝
尽管 α 的取值无限多,但是可能的最优子树是有限的,因此可以利用最优子树序列中每个子树
与一个 α 有一一对应的关系,以及交叉验证来得到最优的子树 T
α
以及对应的剪枝系数 α。
令 α
0
= 0,得到剪枝的起点——T
0
树。
剪枝时,只需要关注当前内部结点 t 和以 t 为根节点的子树 T
t
即可。
对于 T
0
任意内部结点 t,令其作为叶子结点(剪枝后的情形),则对单个叶子结点 t 定义 cost-
complexity measure 如下:
C
α
(t) = C(t) + α
以 t 为根节点的子树 T
t
(剪枝前的情形),其 cost-complexity measure 为:
C
α
(T
t
) = C(T
t
) + α|
˜
T
t
|
当 α = 0 及 α 足够小时,以下不等式成立
C
α
(T
t
) < C
α
(t)
当 α 增大时, 在最小 α 处让以下等式成立的结点称为最弱链接(weakest link),因此 CCP 又称
为 Weakest-Link Cutting。可能存在多个结点在最小 α 处同时达到相等,因此可能有几个最弱
链接结点。
C
α
(T
t
) = C
α
(t)
当 α 继续增大时,该不等式将反向,即 C
α
(T
α
) > C
α
(t)。
只要 α =
C(t)−C(T
t
)
|T
t
|−1
,T
t
与 t 有相同的 cost-complexity measure,而 t 的结点更少,因此 t 比 T
t
更可取,此时对 T
t
进行剪枝,得到 T
1
= T
0
−T
t
。如果存在多个 weakest link,如 t 和 t
′
,则剪
去所有 weakest link,即 T
1
= T
0
− T
t
− T
t
′
。
具体来说,T
t
和 T
t
′
可能存在嵌套关系,如 T
t
′
是 T
t
的子树,此时只需要剪掉 T
t
即可。
T
t
和 T
t
′
也可能是没有公共结点的,此时需要剪掉 T
t
和 T
t
′
。
定义如下函数 g
0
(t),其中 t ∈ T
0
g
0
(t)
(
R(t)−R(T
t
)
|
˜
T
t
|
−1
, t /∈
˜
T
0
+∞, t ∈
˜
T
0
树 T
0
中的 weakest link t
1
对应的最小 g
0
(t) 值为 g
1
(t
1
) = min
t∈T
0
g
0
(t),得到 α
1
= g
0
(t
1
)。
重复上述步骤,使用 T
1
代替 T
0
作为第三轮剪枝的出发点。
计算
在计算方面,我们需要为每个节点存储一些值。
• C(t),结点 t 的 resubstitution error rate,这只需要计算一次。
• C(T
t
),以结点 t 为根节点的子树 T
t
的 resubstitution error rate。剪枝后可能需要更新,因
为剪枝后 T
t
可能会改变。
• |T
t
|,以结点 t 为根节点的子树 T
t
的叶节点总数。剪枝后可能需要对其进行更新。
34

5.7 多变量决策树
CART 剪枝算法
Algorithm 2: CART prune
Input: 基于所有训练数据,使用 CART 算法生成的完整决策树 T
0
1 设 k = 1,T = T
1
2 设 α = +∞
3 自下而上地对各内部结点 t 计算 C (T
t
) , |
˜
T
t
| 以及
g(t) =
C(t) − C (T
t
)
|
˜
T
t
| − 1
α = min(α, g(t))
这里,T
t
表示以 t 为根结点的子树,C (T
t
) 是对训练数据的预测误差,|
˜
T
t
| 是 T
t
的叶结点个数.
4 自上而下地访问内部结点 t,如果有 g(t) = α,进行剪枝,并对叶结点 t 以多数表决法决定其类,得
到树 T.
5 设 k = k + 1, α
k
= α, T
k
= T
6 如果 T
k
不是由根结点及两个叶结点构成的树,则回到步骤 (2); 否则令 T
k
= T
n
7 采用交叉验证法在子树序列 T
0
, T
1
, ··· , T
n
中选取最优子树 T
α
Output: 最优决策树 T
α
在步骤 3 中,自下而上地计算 g(t) 是因为要计算 T
t
的叶子结点数
˜
T
t
。因为任何内部结点的叶
子结点数等于左子结点的叶节点数加上右子结点的叶节点数,而自底向上地计算可以确保先计
算子结点的叶结点数,再计算父结点的叶结点数。
在步骤 4 中,自上而下地剪枝是因为可能存在多个 weakest-link 结点,而剪枝后需要得到最小
的最优子树 T
α
,先剪掉最上层的 weakest-link 结点可以保证最少的剪枝次数,以及最优子树是
最小的。
{α
k
} 是严格递增的序列,因为在每一轮剪枝中,可以得到更小的 α 值的内部结点已经在上一轮
剪枝中被剪掉。
最后一步的交叉验证是对 {α
k
} 序列中每一个 α 进行交叉验证,即采用训练集重新生成 CART
树,使用 {α
k
} 序列中每一个 α 进行剪枝,得到新的 {T
′
α
} 序列。在验证集上测试 {T
′
α
} 序列,
最终得到最佳的 α 值,然后返回 {T
α
} 序列选取 T
α
树。
5.7 多变量决策树
若把每个属性视为坐标空间中的一个坐标轴,则拥有 d 个属性的样本就对应了 d 维空间中的一
个数据点,对样本分类则意味着在这个坐标空间中寻找不同类样本之间的分类边界。
前面提到的决策树都是单变量决策树(univariate decision tree),即在每个内部结点做判定时都
只用到一个属性。单变量决策树所形成的分类边界有一个明显的特点:轴平行 (axis-parallel),即
它的分类边界由若干个与坐标轴平行的分段组成。如图5.2所示。
35

5.8 总结
图 5.2: 单变量决策树的分类边界
这相当于假设样本的各属性之间是没有关联的,所以各坐标轴是相互垂直的。这样有一个弊端:
如果真实分类边界特别复杂,就需要画出很多超平面,在预测时就需要继续大量的属性测试(遍
历决策树)才能得到结果,预测时间开销很大。
若能使用斜的划分边界,即是说每次划分使用多个属性,如图5.3中红色线段所示,则决策树的
计算量将大为减小。
图 5.3: 多变量决策树的划分边界
使用多个属性进行划分结点的决策树称为多变量决策树 (multivariate decision tree)。
在多变量决策树中,内部结点不再是仅对某个属性,而是对属性的线性组合进行测试。换言之,
每个非叶结点是一个形如
P
d
i=1
w
i
a
i
= t 的线性分类器,其中 w
i
是属性 a
i
的权重,w
i
和 t 可
在该结点所含的样本集和属性集上学得。
于是, 与传统的“单变量决策树”不同,在多变量决策树的学习过程中,不是为每个非叶结点寻
找一个最优划分属性,而是试图建立一个合适的线性分类器。
5.8 总结
ID3 (Iterative Dichotomizer 3) 由 Ross Quinlan 在 1986 年提出。ID3 决策树可以是多叉树,不
能处理数值特征,并且某个属性被选为划分属性后,该属性不能再被后面的分支选为划分属性。
ID3 的原始版本不支持剪枝。
C4.5 是 Ross Quinlan 在 1993 年在 ID3 的基础上改进而提出的。C4.5 改用信息增益比作为选
择最佳划分属性的准则,并且支持数值特征和剪枝。相比于 ID3,C4.5 的计算复杂度更低。
决策树算法优点
1. 决策树可解释度高,可以可视化分析,容易提取出规则。
2. 数据不需要归一化或标准化,可以处理缺失值。
36
5.9 PYTHON 代码
3. 预测数据时,计算复杂度为 O(log n),n 为样本数。
4. 既可以处理类别型数据也可以处理数值型数据。
5. 能够处理和预测目标不相关的特征。
6. 对于异常点不敏感。
决策树算法缺点
1. 决策树容易过拟合。
2. 决策树具有高方差,树结构不稳定,相关变量的随机波动可能生成完全不一样的树。
3. 寻找最优决策树是 NP 难问题,使用启发式方法寻找最佳划分,容易陷入局部最优。
4. 决策树不能简单地表示一些比较复杂的问题,如异或。
5. 单调树会忽略特征的相关性。
6. 树模型是分步函数,而不是连续函数。
5.9 Python 代码
import matplotlib.pylab as plt
import numpy as np
def ent(prob_list: list):
return ‐np.sum(np.log2(prob_list) * prob_list)
p_range = np.arange(0.01, 1, 0.01)
ent_result = []
for p in p_range:
prob = [p, 1 ‐ p]
ent_result.append(ent(prob))
plt.title("Entropy of Binomial‐Type Distributions", fontsize=19)
plt.xlabel("Probability", fontdict={"fontsize": 18})
plt.ylabel("Entropy", fontdict={"fontsize": 18})
plt.xticks(fontsize=16)
plt.yticks(fontsize=16)
ax = plt.gca()
ax.spines['top'].set_color('none')
ax.spines['right'].set_color('none')
plt.plot(p_range, ent_result, lw=3)
plt.grid()
plt.savefig('./py_plot/entropy_of_binomial.pdf', bbox_inches='tight')
37
5.9 PYTHON 代码
38
第六章 Perceptron
Perceptron 由 Rosenblatt 于 1957 年提出,是一种简单的线性二分类模型。感知机是支持向量
机和神经网络的基础。可以认为,感知机是最简单的神经网络。感知机可以在输入空间划出一条
直线,或者一个平面、超平面,如果训练集是线性可分的,那么两类样本则分别位于超平面的两
侧。
以下图的感知机为例子:
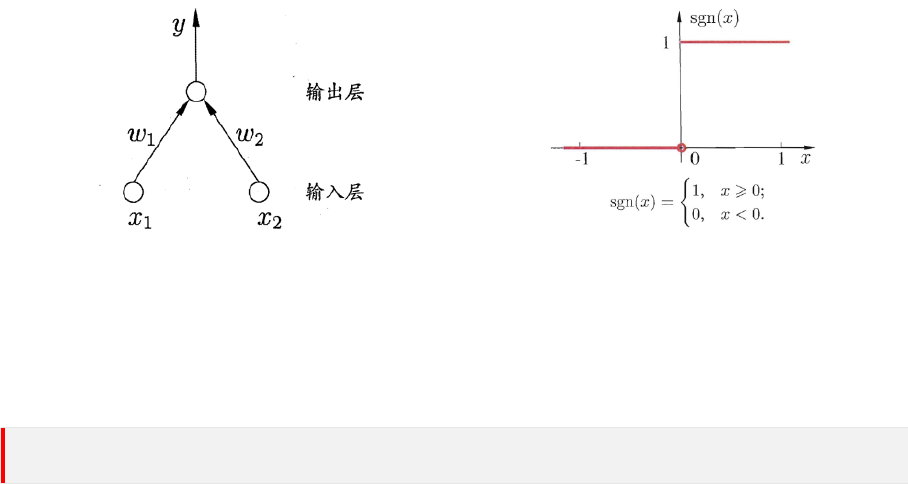
图 6.1: 两个输入神经元的感知机结构示意图
图 6.2: sgn 激活函数
假设输入空间 (特征向量) 为 X ⊆ R
2
,输出空间为 Y = {−1, +1}。输入 x
(
i
)
∈ X 表示第 i 个
样本的特征向量。输出 y
(i)
∈ Y 表示第 i 个样本的类别。显然这个感知机要寻找的直线为:
w
1
x
1
+ w
2
x
2
+ b = 0
这里的 x
1
和 x
2
并不来自输入空间。
而输入空间到输出空间的决策函数为:
ˆy = sgn (f (x)) = sgn
w
⊤
x + b
可以看到,一个感知机主要由如下两部分组成:
• 输入权值和偏置:w 和 b,w 实际上就是感知机划分直线的法向量。
• 激活函数:感知机的激活函数可以有很多选择,比如这里选择的激活函数是 sign 符号函
数。
因为感知机只有一个输出层神经元,其学习能力是非常有限的,只能处理线性可分问题。因此,
感知机被诟病最多的就是其不能处理非线性可分问题。
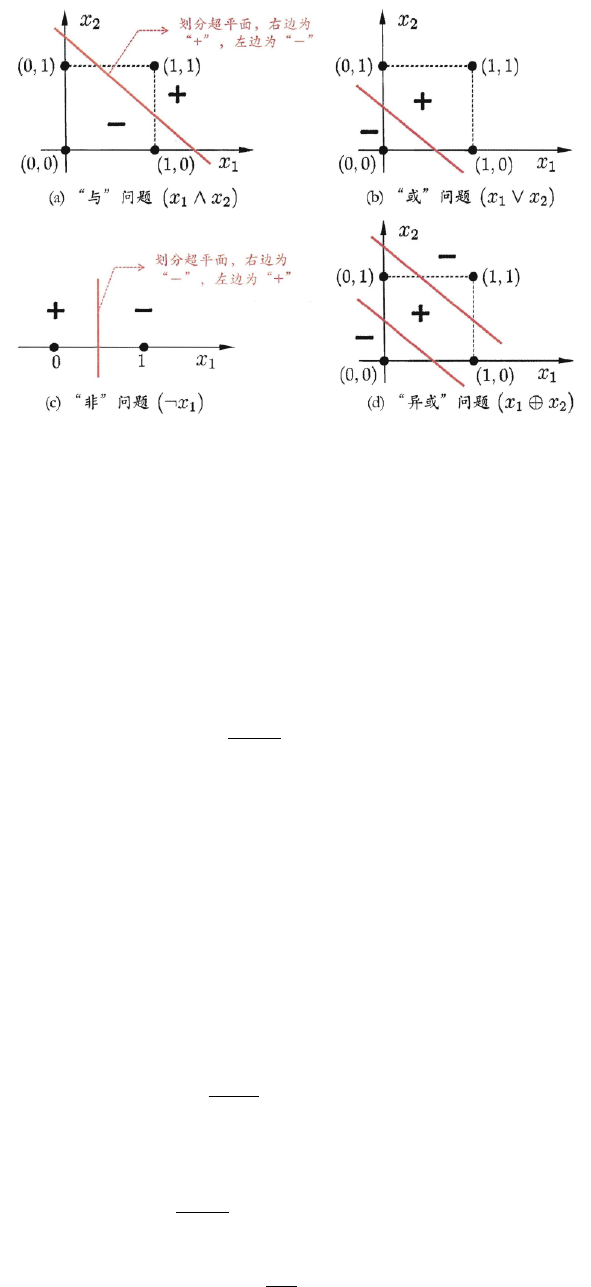
如图10.3所示,“与、或、非”都是线性问题,而“异或”是非线性可分问题,感知机无法处理。
39
6.1 损失函数
图 6.3: 线性可分的“与”“或”“非”问题与非线性可分的“异或”问题
6.1 损失函数
感知机的学习策略是最小化损失函数。损失函数的选择有多种,这里我们采用的是误分类点到
超平面的距离,如下:
1
∥ w ∥
|wx + b|
其中 ||w|| 是 L
2
范数,即是 w 向量的模。
对于正确分类的样本点 (x
(i)
, y
(i)
) 而言:
y
(i)
(wx
(i)
+ b) > 0
所以,对于误分类点 (x
i
, y
i
) 来说:
y
(i)
(wx
(i)
+ b) < 0
误分类点 x
(i)
到超平面的距离为:
−
1
∥ w ∥
y
(i)
(wx
(i)
+ b)
那么,所有误分类的点到超平面的总距离为:
−
1
∥ w ∥
X
x
(i)
ϵM
y
(i)
(wx
(i)
+ b)
由于极值计算不受常量的影响,因此不考虑
1
||w||
,由此得到感知机的损失函数如下:
L(w, b) = −
X
x
(i)
ϵM
y
(i)
(wx
(i)
+ b)
其中 M 为误分类的集合。
可以看出,随时函数 L(w, b) 是非负的。如果没有误分类点,则损失函数的值为 0,而且误分类
点越少,误分类点距离超平面就越近,损失函数值就越小。同时,损失函数 L(w, b) 是连续可导
函数 s。
40
6.2 参数更新
6.2 参数更新
感知器的学习算法是一种错误驱动的在线学习算法 [Rosenblatt, 1958]. 先初始化一个权重向量
w ← 0 (通常是全零向量),然后每次分错一个样本 (x, y) 时,即 yw
⊤
x < 0,就用这个样本来更
新权重。
w ← w + yx
实际上,这就是随机梯度下降的策略,其每次更新的梯度为
∂L(w; x, y)
∂w
=
0 if yw
⊤
x > 0
−yx if yw
⊤
x < 0
极小化过程不是一次所有误分类点的梯度下降,选取当前误分类点使其梯度下降。使用的规则
为 θ := θ −η∇
θ
ℓ(θ),其中 η 是步长,即学习率,∇
θ
ℓ(θ) 是梯度。因此,每次更新权重的公式为:
w ← w + ηyx
b ← b + ηy
我们可以从几何的角度去理解这个更新过程,在此之前,我们可能需要一点点先验知识。
w
⊤
x 是一个内积,在欧几里得空间,点积可以被定义为:
w
⊤
x = |w||x|cos θ
w 是划分直线的法向量,但我们知道直线的法向量是可以有两个方向的,即向左或向右,
那么 w 到底是指哪个方向的法向量呢?从前面的决策函数(即分类规则)可以看出,法向
量 w 指向正类(+1)所在的方向。
为了方便讨论,我们将 w
⊤
x + b 改写为 w
⊤
x,这是完全没有问题的,只需要将 w 和 x
各自增加一个维度即可。这种写法的好处是,我们可以直接从 w 和 x 的内积的符号去判
断分类结果,
如果一个正类的点被误分为负类,即
w
⊤
x
<
0
,那表示
w
和
x
夹角大于
90
度。所以,修正
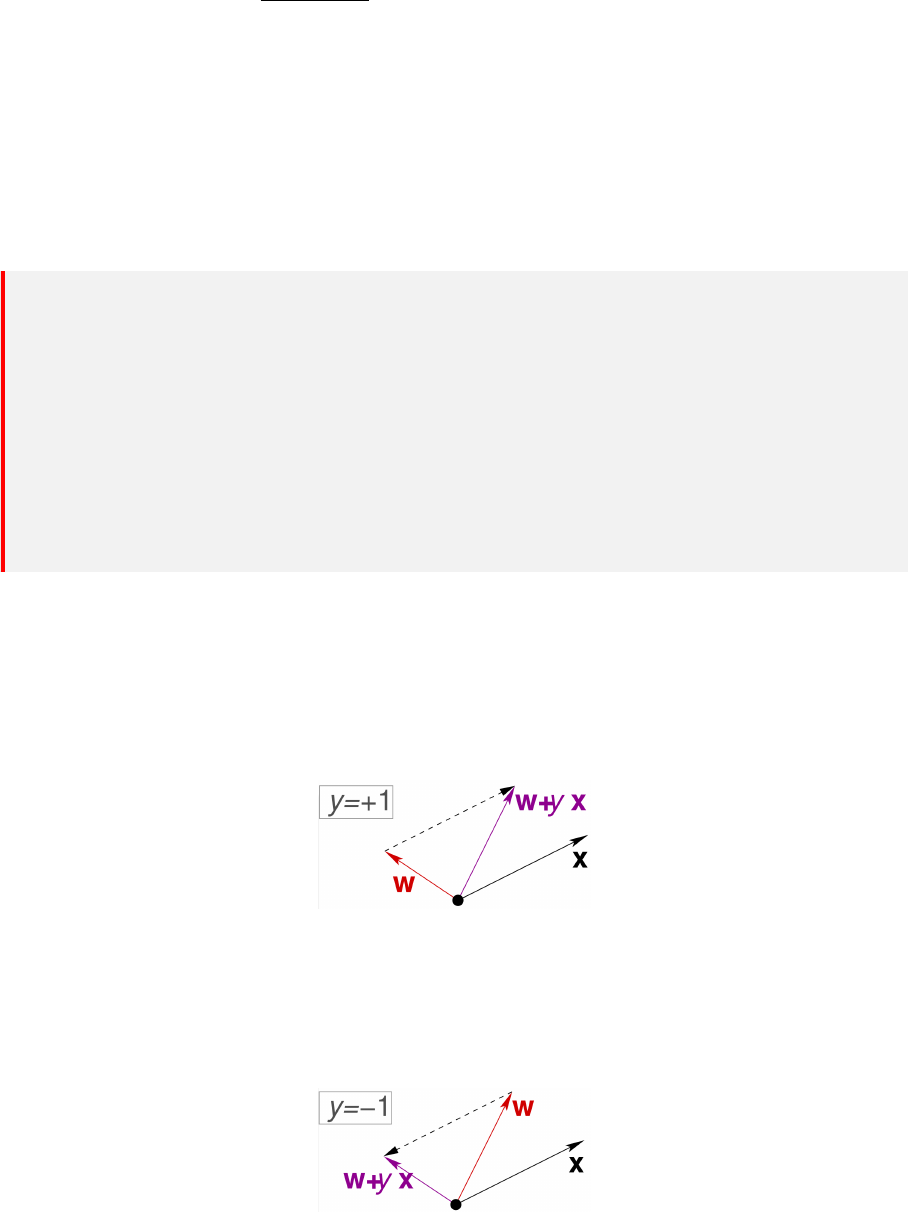
的方法就是使 w 和 x 夹角小于 90 度,从而让法向量指向该正类点所在的一侧,通常做法是
w ← w + yx, y = 1,如下图所示。根据向量加法的平行四边形法则,一次更新,就可以使得新
的法向量 w + x 与 x 的夹角小于 90 度,这就对该误分类点完成了修正。但是由于学习率的存
在,实际上更新后的法向量为 w + ηx,因此一次更新可能不会让法向量和误分类点的夹角小于
90 度,需要多次更新才能达到目的。
同理,如果一个负类点被误分为正类,即 w
⊤
x > 0,那表示 w 和 x 夹角小于 90 度。修正的方
法就是使 w 和 x 夹角小大于 90 度。通常做法是 w ← w + yx, y = −1 。如下图所示。根据向
量减法的三角形法则,一次更新,就可以使得新的法向量 w − x 与 x 的夹角大于 90 度,这就
对该误分类点完成了修正。同样由于学习率的存在,实际上可能需要多次更新才能达到目的。
41

6.2 参数更新
我们可以证明,当学习率足够小的时候,划分直线与误分类点的距离在参数更新后会变得更小
(这里不在意参数更新后,误分类点是否被正确分类)。这是感知机参数更新的性质,具体证明过
程如下:
对于某个误分类点
−→
x
i
, ˜y
i
, 假设它被选中用于更新参数。
1. 假设迭代之前,分类超平面为 S, 该误分类点距超平面的距离为 d
2. 假设迭代之后,分类超平面为 S
′
, 该误分类点距超平面的距离为 d
′
则:
∆d = d
′
− d =
1
−→
w
′
2
−→
w
′
·
−→
x
i
+ b
′
−
1
∥
−→
w ∥
2
−→
w ·
−→
x
i
+ b
= −
1
−→
w
′
2
˜y
i
−→
w
′
·
−→
x
i
+ b
′
+
1
∥
−→
w ∥
2
˜y
i
−→
w ·
−→
x
i
+ b
≃ −
˜y
i
∥
−→
w ∥
2
−→
w
′
−
−→
w
·
−→
x
i
+
b
′
− b
= −
˜y
i
∥
−→
w ∥
η˜y
i
−→
x
i
·
−→
x
i
+ η˜y
i
= −
˜y
2
i
∥
−→
w ∥
2
η
−→
x
i
·
−→
x
i
+ 1
< 0
因此有 d
′
< d 这里要求
−→
w
′
≃
−→
w , 因此步长 η 要相当小。
具体的感知器参数学习策略如下图所示(摘自邱锡鹏的《神经网络与深度学习》):
图 6.4: 二分类感知器的参数学习算法
在有的文章中(例如周志华的《机器学习》),最后得到的更新公式为:
w ← w + α∆w
b ← b + ∆b
其中,∆w = α(y − ˆy)x,∆b = α(y − ˆy)。
42

6.3 感知器收敛性
这是因为它将样本的类别映射为 0 和 1,同时采取平方和损失函数,所以权值更新的公式不一
样,不过思想都是一样的。这种情况下的更新公式推导可以参考这篇文章《机器学习 _ 感知机》
。
6.3 感知器收敛性
感知机的迭代一定会停下来吗?由感知机算法的定义,可以知道,当找到一条直线,能将平面上
的点都分类正确,那么感知机就会停止。显然,要达到这个终止条件,训练集必须是线性可分的。
如果训练集不是线性可分的,那么上述的感知机算法永远不会停止。
[Noviko, 1963] 证明了对于两类问题,如果训练集是线性可分的,那么感知器算法可以在有限
次迭代后收敛。然而,如果训练集不是线性可分的,那么这个算法则不能确保会收敛。
当数据集是两类线性可分时, 对于训练集 D =
x
(n)
, y
(n)
N
n=1
, 其中 x
(n)
为样本的增广特征向
量, y
(n)
∈ {−1, 1}, 那么存在一个正的常数 γ(γ > 0) 和权重向量 w
∗
, 并且 ∥w
∗
∥ = 1, 对所有 n
都满足 (w
∗
)
⊤
y
(n)
x
(n)
≥ γ. 我们可以证明如下定理.
定理 6.1. 感知器收敛性
给定训练集 D =
x
(n)
, y
(n)
N
n=1
, 令 R 是训练集中最大的特征向量的模,即
R = max
n
x
(n)
如果训练集 D 线性可分,两类感知器的参数学习算法 3.1 的权重更新次数不超过
R
2
γ
2
详细的证明过程参考邱锡鹏的《神经网络与深度学习》第 3.4.2 节(感知器的收敛性)。
6.4 感知机的缺陷
虽然感知器在线性可分的数据上可以保证收敛,但其存在以下不足:
(1)在数据集线性可分时,感知器虽然可以找到一个超平面把两类数据分开,但并不能保证其泛
化能力。
(2)感知器对样本顺序比较敏感.每次迭代的顺序不一致时,找到的分割超平面也往往不一致。
(3)如果训练集不是线性可分的,就永远不会收敛。
43
6.4 感知机的缺陷
44
第三部分
机器学习高阶
优化方法
45
第七章 凸优化基础概念
7.1 凸集
定义7.1 直线和线段: 设 x
1
̸= x
2
为 R
n
空间中的两个点,那么具有下列形式的点
y = θx
1
+ (1 − θ)x
2
, θ ∈ R
y = x
2
+ θ (x
1
− x
2
)
组成一条穿越 x
1
和 x
2
的直线。如果参数 θ 的值在 0 和 1 之间变动,则构成 x
1
和 x
2
之间的
线段。
定义7.2 仿射集合: 如果通过集合 C ⊆ R
n
中任意两个不同点的直线仍然在集合 C 中,那么
称集合 C 是仿射的。也就是说,C ⊆ R
n
是仿射的等价于:对于任意 x
1
, x
2
∈ C 及 θ ∈ R 有
θx
1
+ (1 − θ)x
2
∈ C 。换而言之,C 包含了 C 中任意两点的系数之和为 1 的线性组合。
定义7.3 仿射组合:如果 θ
1
+ ···+ θ
k
= 1,我们称具有 θ
1
x
1
+ ···+ θ
k
x
k
形式的点为 x
1
, ··· , x
k
的仿射组合。
因此,仿射集合又可以被定义如下。
定义7.4 仿射集合: 仿射集合包含其中任意两点的仿射组合。
根据定义7.4,我们可以归纳出以下结论:
一个仿射集合包含其中任意点的仿射组合,即如果 C 是一个仿射集合,x
1
, ··· , x
k
∈ C, 并且
θ
1
+ ··· + θ
k
= 1, 那么 θ
1
x
1
+ ··· + θ
k
x
k
仍然在 C 中。
定义7.5 仿射包: 我们称由集合 C ⊆ R
n
中的点的所有仿射组合组成的集合为 C 的仿射包,记
为 aff C
aff C = {θ
1
x
1
+ ··· + θ
k
x
k
| x
1
, ··· , x
k
∈ C, θ
1
+ ··· + θ
k
= 1}
仿射包是包含 C 的最小的仿射集合。
定义7.6 凸集: 设集合 S ⊂ R
n
,如果对任意 x
1
, x
2
∈ S, 有
θx
1
+ (1 − θ)x
2
∈ S, ∀θ ∈ [0, 1]
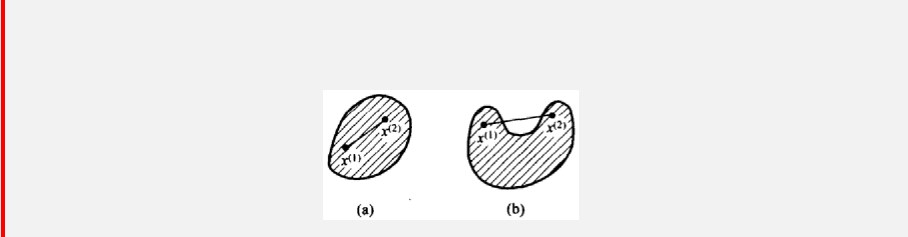
则称 S 是凸集。
换而言之,对于 n 维欧氏空间 R
n
中一个集合 S,若对 S 中任意两点,联结它们的线段仍
属于 S,则 S 是凸集。
47

7.2 重要的凸集
a 是凸集,b 是非凸集。
定义7.7 凸组合: 如果 θ
1
+ ···+ θ
k
= 1,并且 θ
i
⩾ 0, i = 1, ··· , k,我们称点 θ
1
x
1
+ ···+ θ
k
x
k
为点 x
1
, ··· , x
k
的一个凸组合。
显然,从统计学的角度看,点的凸组合可以看作它们的加权平均(期望)。
与仿射集合类似,一个集合是凸集等价于集合包含其中所有点的凸组合。
定义7.8 凸包: 我们称集合 C 中所有点的凸组合的集合为其凸包,记为 conv C:
conv C = {θ
1
x
1
+ ··· + θ
k
x
k
| x
i
∈ C, θ
i
⩾ 0, i = 1, ··· , k, θ
1
+ ··· + θ
k
= 1}
顾名思义,凸包 conv C 总是凸的。它是包含 C 的最小的凸集。
定义7.9 锥: 如果对于任意 x ∈ C 和 θ ⩾ 0 都有 θx ∈ C, 我们称集合 C 是锥或者非负齐次。
定义7.10 凸锥: 如果集合 C 是锥,并且是凸的,则称 C 为凸锥,即对于任意 x
1
, x
2
∈ C 和
θ
1
, θ
2
⩾ 0 都有
θ
1
x
1
+ θ
2
x
2
∈ C
在几何上,具有此类形式的点构成了二维的扇形,这个扇形以 0 为顶点,边通过 x
1
和 x
2
(如
图7.1所示)。
图 7.1: 二维凸锥
定义7.11 锥组合: 具有 θ
1
x
1
+ ··· + θ
k
x
k
, θ
1
, ··· , θ
k
⩾ 0 形式的点称为 x
1
, ··· , x
k
的锥组合
(或非负线性组合)。
如果 x
i
均属于凸锥 C,那么,x
i
的每一个锥组合也在 C 中。反言之,集合 C 是凸雉的充要条
件是它包含其元素的所有雉组合。
定义7.12 锥包: 集合 C 的锥包是 C 中元素的所有雉组合的集合,即
{θ
1
x
1
+ ··· + θ
k
x
k
| x
i
∈ C, θ
i
⩾ 0, i = 1, ··· , k}
它是包含 C 的最小的凸锥。
7.2 重要的凸集
命题1 射线 S = {x | x
0
+ λd, λ ⩾ 0} 是凸集,其中,d 是给定的非零向量,x
0
为定点(射线的
顶点)。
证明. 对任意 x
1
, x
2
∈ S 和每一个数 λ ∈ [0, 1], 有
x
1
= x
0
+ λ
1
d, x
2
= x
0
+ λ
2
d
其中 λ
i
, λ
2
∈ [0, 1],因而
48

7.3 保持凸性的运算
λx
1
+ (1 − λ)x
2
= λ (x
0
+ λ
1
d) + (1 − λ) (x
0
+ λ
2
d)
= x
0
+ [λλ
1
+ (1 − λ)λ
2
] d
注意到 λλ
1
+ (1 − λ)λ
2
⩾ 0, 故 λx
1
+ (1 − λ)x
2
∈ S。
一条射线是凸的,但不是仿射的。如果射线的基点 x
0
是 0,则它是凸雉。类似地,一条线
段是凸的,但不是仿射的,也不是凸锥。
若 A 是 m × n 矩阵, b ∈ R
n
, 则集合
S = {x ∈ R
n
| Ax = b}
是凸集。
命题2 超平面 H =
x | p
T
x = α
是凸集,其中 p ∈ R
n
是非零向量,称为超平面的法向量,α
为实数。事实上,对任意 x
1
, x
2
∈ H 和每一个 θ ∈ [0, 1],有
p
T
[θx
1
+ (1 − θ)x
2
] = α
故 θx
1
+ (1 − θ)x
2
∈ H
证明.
p
T
[θx
1
+ (1 − θ)x
2
] = θp
T
x
1
+ p
T
x
2
− θp
T
x
2
= θα + α − θα
= α
一个超平面将 R
n
划分为两个半空间。(闭的) 半空间是具有下列形式的集合,
x | p
T
x ⩽ α
其中 p ̸= 0。
命题3 闭半空间 H
−
=
x | p
T
x ⩽ β
和 H
+
=
x | p
T
x ⩾ β} 为凸集。开半空间
◦
H
−
=
x | p
T
x < β
和
◦
H
+
=
x | p
T
x > β
为凸集。
证明. 类似于命题 1。
7.3 保持凸性的运算
7.3.1 交集
交集运算是保凸的:如果 S
1
和 S
2
是凸集,那么 S
1
∩ S
2
也是凸集。这个性质可以扩展到无穷
个集合的交
:
如果对于任意
α
∈ A
, S
α
都是凸的,那么
∩
α∈A
S
α
也是凸集。
7.3.2 仿射函数
定义7.13 仿射函数: 函数 f : R
n
→ R
m
是仿射的,如果它是一个线性函数和一个常数的和,即
具有 f(x) = Ax + b 的形式,其中 A ∈ R
m×n
, b ∈ R
m
。
假设
S
⊆
R
n
是凸的,并且
f
:
R
n
→
R
m
是仿射函数。那么,
S
在
f
下的象
f(S) = {f (x) | x ∈ S}
49
第八章 梯度下降
8.1 梯度下降原理
f(θ) ≈ f (θ
0
) + (θ − θ
0
) · ∇f(θ
0
)
θ −θ
0
是微小向量,它的大小就是步进长度,即学习率 α,α 是一个标量,而 θ − θ
0
的单位向
量用 v 表示,因此 θ − θ
0
可表示为:
θ − θ
0
= αv
特别需要注意的是,θ −θ
0
不能太大,因为太大的话,线性近似就不够准确,一阶泰勒近似也不
成立了,替换之后,f(θ) 的表达式为:
f(θ) ≈ f (θ
0
) + αv · ∇f (θ
0
)
局部下降的目的是希望每次 θ 更新,都能让函数值 f(θ) 变小。也就是说,上式中,我们希望
f(θ) ≤ f (θ
0
)。则有:
f(θ) − f (θ
0
) ≈ αv · ∇f (θ
0
) ≤ 0
因为 α 为标量,且一般设定为正值,所以可以忽略,不等式变成了:
v · ∇f(θ
0
) ≤ 0
上面这个不等式非常重要!v 和 ∇f(θ
0
) 都是向量,∇f (θ
0
) 是当前位置的梯度方向,v 表示下
一步前进的单位向量,是需要我们求解的,有了它,就能根据 θ − θ
0
= αv 来确定 θ 的值了。
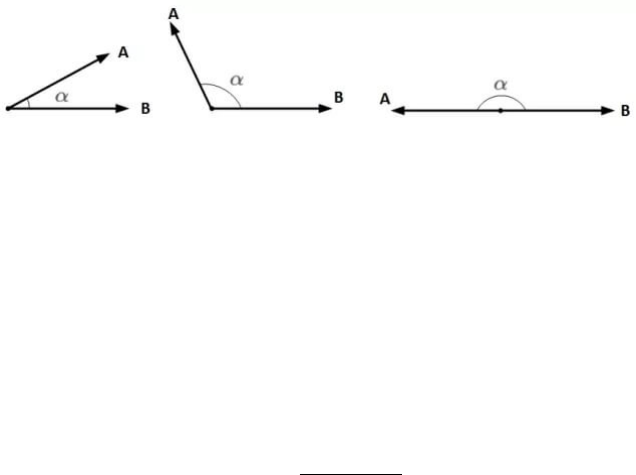
想要两个向量的乘积小于零,我们先来看一下两个向量乘积包含哪几种情况:
上图中,A 和 B 均为向量,α 为两个向量之间的夹角。A 和 B 的乘积为:
A · B = ||A|| · ||B||· cos(α )
||A|| 和 ||B|| 均为标量,在 ||A|| 和 ||B|| 确定的情况下,只要 cos(α) = −1,即 A 和 B 完全
相反,就能让 A 和 B 的向量乘积最小(负最大值)。
顾名思义,当 v 和 ∇f (θ
0
) 互为反向,即当 v 为当前梯度方向的负方向的时候,能让 v ·∇f(θ
0
)
最大程度地小,也就保证了 v 的方向是局部下降最快的方向。
知道了 v 是 ∇f (θ
0
) 的反方向后,可直接得到:
v = −
∇f(θ
0
)
||∇f(θ
0
)||
51
第九章 Backpropagation
9.1 神经网络
神经网络是按照一定规则连接起来的多个神经元。神经网络按照层级来布局神经元。
• 最左边的层叫做输入层(input layer),主要负责接收输入数据。
• 最右边的层叫输出层(output layer),可以从这一层获取神经网络输出数据。
• 输入层与输出层之间的层叫做隐藏层,可以包含多个隐藏层,之所以叫做隐藏层,是因为
它们对于外部来说是不可见的。
全连接神经网络的特征如下:
1. 位于同一层的各个神经元没有任何连接。
2. 位于第 N 层的每个神经元都与第 N-1 层的所有神经元相连,也就是全连接(Full Connec-
tion),第 N-1 层神经元的输出就是第 N 层神经元的输入。
3. 全连接的每个连接都有一个权值。
事实上还存在很多其它结构的神经网络,比如卷积神经网络 (CNN)、循环神经网络 (RNN),他
们都具有不同的连接规则。
9.2 基本函数
推导 BP 算法的过程中需要注意几个要点:
• 网络函数
• 激活函数:sigmoid
• 误差函数:平方误差
• 优化方法:梯度下降,降低误差大的网络的权值,增加误差小的网络的权值。
下面先来介绍几个在神经网络反向传播算法的推导过程中用到的几个函数:
1.Network function(网络函数)
The network is a particular implementation of a composite function from input to output space,
which we call the network function.
h(x) = w
T
x =
n
X
i=1
w
i
x
i
2.Activation function(激活函数)
这里使用的激活函数是 Sigmoid 函数:
53
9.3 前向传播
y = f (z) =
1
1 + e
−z
3.Error function
(误差函数)
采用平方误差作为目标函数:
E =
1
2
n
X
i=1
[t
i
− y
i
]
2
其中 t
i
为真实值,y
i
为计算值,等于 y
i
= f(h(x
i
))。下面对 BP 算法的计算过程进行推导。
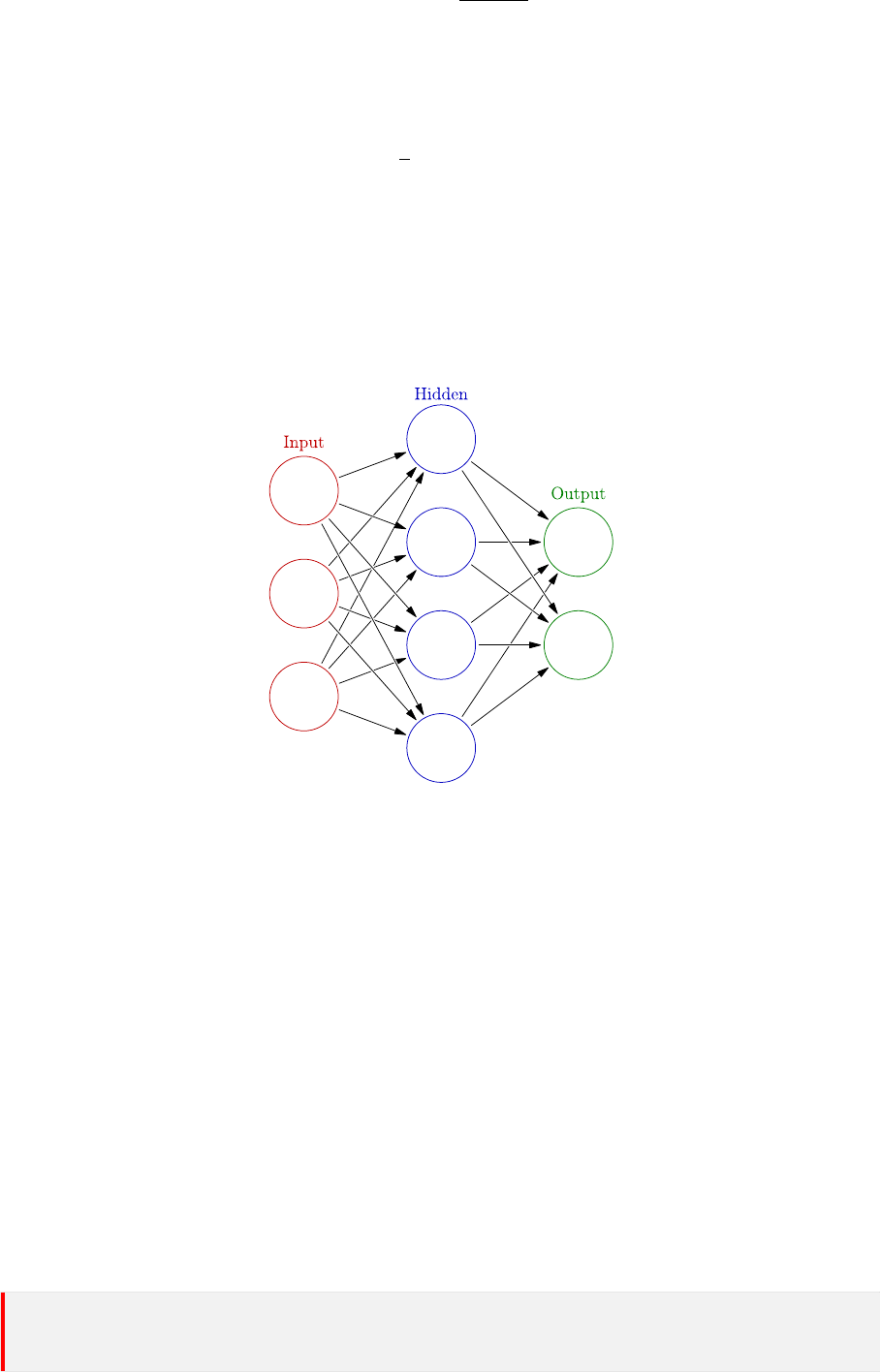
9.3 前向传播
图 9.1: 神经网络示意图
上图展示的是一个经典的三层神经网络,包括输入层、隐藏层、输出层。为了体现一般性,现在
用数学语言进行描述:
给定一个训练集 {(x
1
, t
1
) , (x
2
, t
2
) , . . . , (x
n
, t
n
)},目标变量 t
i
的取值可以有多个,其中 x
i
是一
个 m 维向量(对应输入层的 m 个神经元),表达式为 x
i
= (x
i1
, x
i2
, ··· , x
im
)。我们将输入层、
隐藏层、输出层合并在一起,就形成了一个 network。在这个 network 里,除输入层外,其他层
上的每个神经元都是上一层神经元的全连接,不同的是全连接的权值不一样。现在,我们需要通
过训练,来求出各个神经元的权重值,也就是 w。
那么现在的问题是,这些权值应该如何计算呢?
刚刚说到,除输入层外,其他层上的每个神经元都是上一层神经元的全连接, 比如隐藏层 h
1
,是
隐藏层的第一个神经元,它的输出值是输入层的全连接,即:
h
1
= f
w
1
1
· x
(9.1)
net
1
1
= w
1
11
x
1
+ w
1
12
x
2
+ w
1
13
x
3
+ b
1
1
(9.2)
行标表示当前层的第几个节点,列标表示上一层的第几个节点,上标表示当前是第几个隐
藏层
其中 f 为 sigmoid 函数,w
1
ij
表示隐藏层的第 i 个节点与输入层的第 j 个节点的权重值,b
1
i
表
示第 i 个隐藏层全连接中的偏置,x
i
为输入层的值,即样本的输入值。
54
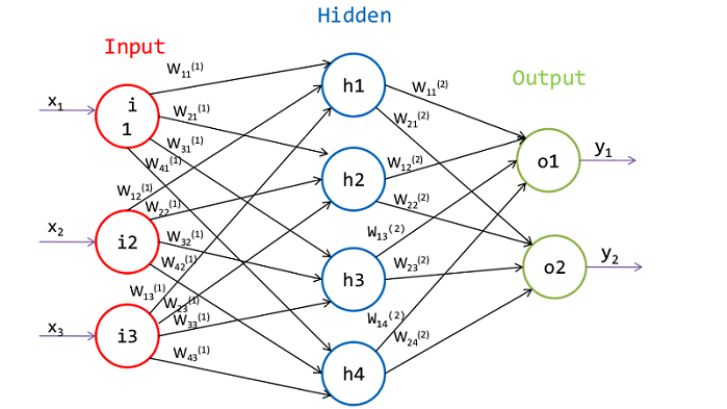
9.3 前向传播
图 9.2: 前向传播
类似的,可以计算出 h
2
、h
3
、h
4
:
h
1
= f
w
1
11
x
1
+ w
1
12
x
2
+ w
1
13
x
3
+ b
1
1
h
2
= f
w
1
21
x
1
+ w
1
22
x
2
+ w
1
23
x
3
+ b
1
2
h
3
= f
w
1
31
x
1
+ w
1
32
x
2
+ w
1
33
x
3
+ b
1
3
h
4
= f
w
1
41
x
1
+ w
1
42
x
2
+ w
1
43
x
3
+ b
1
4
(9.3)
因此,我们可以将隐藏层表示为如下通式:
h = f(net
1
) = f
w
1
1
· x
(9.4)
w
1
=
w
1
1
w
1
2
w
1
2
w
1
3
w
1
4
=
w
1
11
, w
1
12
, w
1
13
, b
1
1
w
1
21
, w
1
22
, w
1
23
, b
1
2
w
1
31
, w
1
32
, w
1
33
, b
1
3
w
1
41
, w
1
42
, w
1
43
, b
1
4
(9.5)
对于输出层,也是同样的计算方式,只不过对于输出层而言,它们的输入为隐藏层的输出,即 h
,输出层的表达式为:
y = f
w
(2)
· h
w
(2)
=
"
w
(2)
1
w
(2)
2
#
=
"
w
(2)
11
, w
(2)
12
, w
(2)
13
, w
(2)
14
, b
(2)
1
w
(2)
21
, w
(2)
22
, w
(2)
23
, w
(2)
24
, b
(2)
1
#
y
1
= f
w
(2)
11
h
1
+ w
(2)
12
h
2
+ w
(2)
13
h
3
+ w
(2)
13
h
4
+ b
(2)
1
y
2
= f
w
(2)
21
h
1
+ w
(2)
22
h
2
+ w
(2)
23
h
3
+ w
(2)
13
h
4
+ b
(2)
2
即:
y
i
= f
net
(2)
i
= f
X
j=1
w
(2)
ij
h
j
+ b
(2)
j
(9.6)
上述部分属于 feed-forward 部分,从前往后依次计算出各个输出层,最后求得 y。但此时这些权
值还未知。
55

9.4 反向传播
9.4 反向传播
首先,对所有的权值 w 给定一个初始值,然后根据前向传播的方式来计算出输出值 y,为了评估
此次训练模型是否合理,我们取网络所有输出层节点的误差平方和作为目标函数,对于样本 k,
其误差表达式为:
E
k
=
1
2
output
X
j=1
[t
j
− y
j
]
2
(9.7)
有了目标函数之后,现在我们采用梯度下降来寻找最优解。
9.4.1 输出层
对于输出层节点,第 i 个输出节点与第 j 个隐藏节点的权值更新规则为:
w
(2)
ij
← w
(2)
ij
− η
∂E
k
∂w
(2)
ij
(9.8)
其中 η 为学习率,由于 E
k
是 y
i
的函数,y
i
是 net
(2)
的函数,net
(2)
是 w
ij
的函数,根据链式
求导法则,有:
∂E
k
∂w
(2)
ij
=
∂E
k
∂y
i
∂y
i
∂net
(2)
i
∂net
(2)
i
∂w
(2)
ij
(9.9)
根据上述公式,可以分别求出偏导数:
∂E
k
∂y
i
=
∂
∂y
i
1
2
outputs
X
j
(t
j
− y
j
)
2
=
∂
∂y
i
1
2
(t
j
− y
j
)
2
j=i
+
∂
∂y
i
1
2
outputs
X
j
(t
j
− y
j
)
2
j̸=i
=
∂
∂y
i
1
2
(t
i
− y
i
)
2
+ 0
= −(t
i
− y
i
)
∂y
i
∂net
(2)
i
= y
i
(1 − y
i
)
∂net
(2)
i
∂w
(2)
ij
= h
j
(9.10)
∂y
i
∂net
(2)
i
就是激活函数求导:
y = f (z) =
1
1 + e
−z
f
′
(z) =
e
−z
(e
−z
+ 1)
2
=
1
1 + e
−z
−
1
1 + e
−z
2
= y − y
2
(9.11)
56

9.5 权值更新归纳
由此可得,
∂E
k
∂w
(2)
ij
= −(t
i
− y
i
) · y
i
(1 − y
i
) · h
j
(9.12)
9.4.2 隐藏层
首先,对于隐藏层的任意一个神经元,输出层的每个神经单元的误差对其都有影响。因此,对于
隐藏层第 i 个神经元,它与输入层的第 j 个神经元的权值更新规则为:
w
(1)
ij
← w
(1)
ij
− η
∂E
k
∂w
ij
(9.13)
接着由链式法则,我们对上面红色部分进行展开:
∂E
k
∂w
(1)
ij
=
∂
∂w
(1)
ij
outputs
X
s
E
s
!
=
outputs
X
s
∂E
s
∂y
s
y
s
∂net
(2)
s
∂net
(2)
s
∂h
i
∂h
i
∂net
(1)
i
∂net
(1)
i
∂w
ij
=
outputs
X
s
−δ
s
·
∂net
(2)
i
∂h
i
∂h
i
∂net
(1)
i
∂net
(1)
i
∂w
(1)
ij
!
=
outputs
X
s
−δ
s
· w
(2)
si
·
∂h
i
∂net
(1)
i
∂net
(1)
i
∂w
(1)
ij
!
=
outputs
X
s
−δ
s
· w
(2)
si
· h
i
(1 − h
i
) ·
∂net
(1)
i
∂w
(1)
ij
!
=
outputs
X
s
−δ
s
w
(2)
si
h
i
(1 − h
i
) x
j
= −h
i
(1 − h
i
)
outputs
X
s
δ
s
w
(2)
si
!
x
j
(9.14)
代入到上式,得到隐藏层的权值更新公式:
w
(1)
ij
= w
(1)
ij
+ ηh
i
(1 − h
i
)
outputs
X
s
δ
s
w
si
!
x
j
(9.15)
令 δ
i
=
∂E
k
∂net
i
= −h
i
(1 − h
i
) (
P
s
δ
s
w
si
),则公式简化为:
w
(1)
ij
= w
(1)
ij
− ηδ
i
x
j
(9.16)
9.5 权值更新归纳
通过 BP 推导,现在我们知道如何更新权值了,下面来总结一下。假定每个节点的误差项为 δ
i
,
不管是隐藏节点还是输出节点,其输出值统一使用 x
j
来表示,那么权值更新规则为:
w
ij
← w
ij
− ηδ
i
x
j
(9.17)
当节点为输出层神经元时,
δ
i
= −y
i
(1 − y
i
)(t
i
− y
i
) (9.18)
57
9.5 权值更新归纳
当节点为隐藏层神经元时,
δ
i
= −h
i
(1 − h
i
)
X
s
δ
s
w
si
!
(9.19)
其中,δ
i
是节点的误差项,y
i
是输出节点的输出值,t
i
是样本 i 对应的目标值,h
i
为隐藏节点
的输出值。权值更新归纳
58
第四部分
神经网络
59
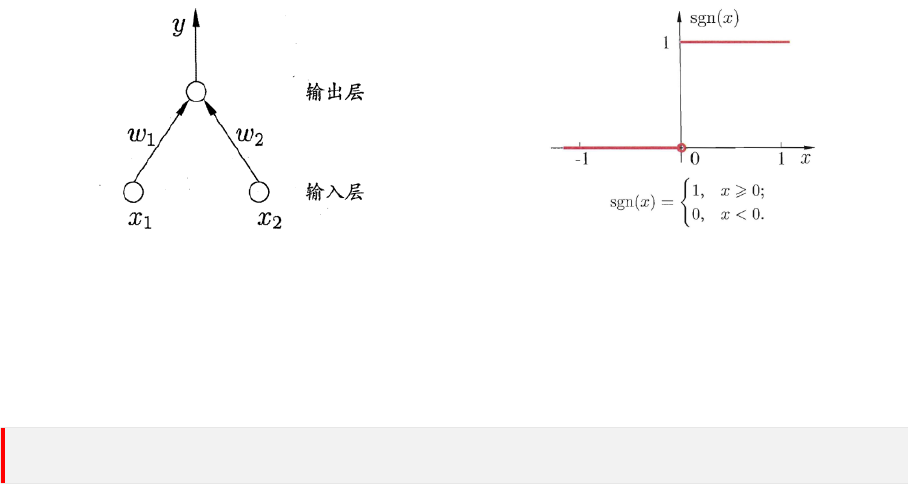
第十章 Perceptron
Perceptron 由 Rosenblatt 于 1957 年提出,是一种简单的线性二分类模型。感知机是支持向量
机和神经网络的基础。可以认为,感知机是最简单的神经网络。感知机可以在输入空间划出一条
直线,或者一个平面、超平面,如果训练集是线性可分的,那么两类样本则分别位于超平面的两
侧。
以下图的感知机为例子:
图 10.1: 两个输入神经元的感知机结构示意图
图 10.2: sgn 激活函数
假设输入空间 (特征向量) 为 X ⊆ R
2
,输出空间为 Y = {−1, +1}。输入 x
(
i
)
∈ X 表示第 i 个
样本的特征向量。输出 y
(i)
∈ Y 表示第 i 个样本的类别。显然这个感知机要寻找的直线为:
w
1
x
1
+ w
2
x
2
+ b = 0
这里的 x
1
和 x
2
并不来自输入空间。
而输入空间到输出空间的决策函数为:
ˆy = sgn (f (x)) = sgn
w
⊤
x + b
可以看到,一个感知机主要由如下两部分组成:
• 输入权值和偏置:w 和 b,w 实际上就是感知机划分直线的法向量。
• 激活函数:感知机的激活函数可以有很多选择,比如这里选择的激活函数是 sign 符号函
数。
因为感知机只有一个输出层神经元,其学习能力是非常有限的,只能处理线性可分问题。因此,
感知机被诟病最多的就是其不能处理非线性可分问题。
如图10.3所示,“与、或、非”都是线性问题,而“异或”是非线性可分问题,感知机无法处理。
61
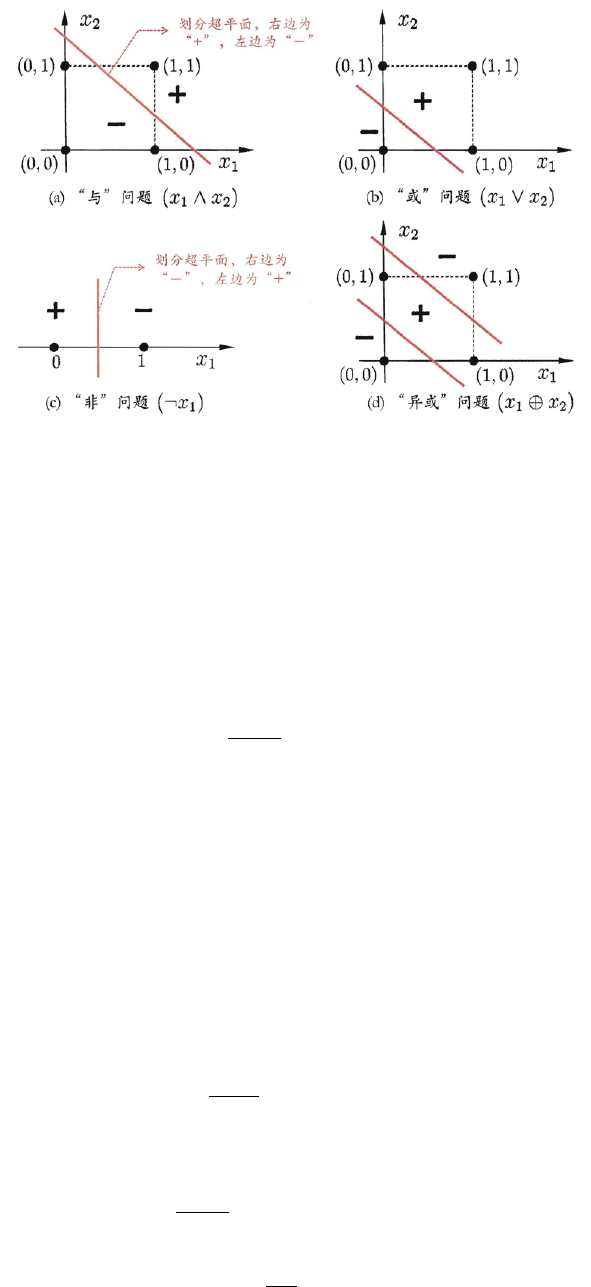
10.1 损失函数
图 10.3: 线性可分的“与”“或”“非”问题与非线性可分的“异或”问题
10.1 损失函数
感知机的学习策略是最小化损失函数。损失函数的选择有多种,这里我们采用的是误分类点到
超平面的距离,如下:
1
∥ w ∥
|wx + b|
其中 ||w|| 是 L
2
范数,即是 w 向量的模。
对于正确分类的样本点 (x
(i)
, y
(i)
) 而言:
y
(i)
(wx
(i)
+ b) > 0
所以,对于误分类点 (x
i
, y
i
) 来说:
y
(i)
(wx
(i)
+ b) < 0
误分类点 x
(i)
到超平面的距离为:
−
1
∥ w ∥
y
(i)
(wx
(i)
+ b)
那么,所有误分类的点到超平面的总距离为:
−
1
∥ w ∥
X
x
(i)
ϵM
y
(i)
(wx
(i)
+ b)
由于极值计算不受常量的影响,因此不考虑
1
||w||
,由此得到感知机的损失函数如下:
L(w, b) = −
X
x
(i)
ϵM
y
(i)
(wx
(i)
+ b)
其中 M 为误分类的集合。
可以看出,随时函数 L(w, b) 是非负的。如果没有误分类点,则损失函数的值为 0,而且误分类
点越少,误分类点距离超平面就越近,损失函数值就越小。同时,损失函数 L(w, b) 是连续可导
函数 s。
62
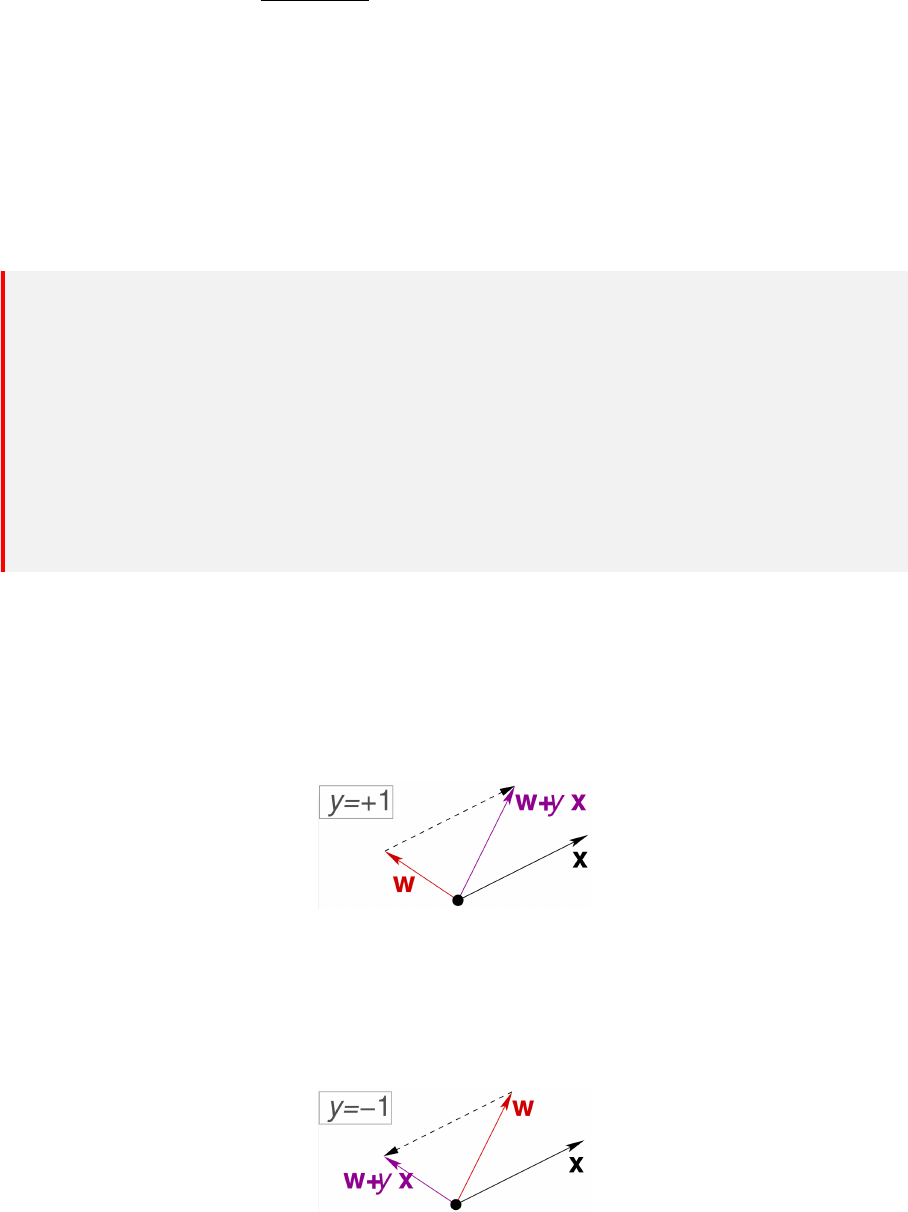
10.2 参数更新
10.2 参数更新
感知器的学习算法是一种错误驱动的在线学习算法 [Rosenblatt, 1958]. 先初始化一个权重向量
w ← 0 (通常是全零向量),然后每次分错一个样本 (x, y) 时,即 yw
⊤
x < 0,就用这个样本来更
新权重。
w ← w + yx
实际上,这就是随机梯度下降的策略,其每次更新的梯度为
∂L(w; x, y)
∂w
=
0 if yw
⊤
x > 0
−yx if yw
⊤
x < 0
极小化过程不是一次所有误分类点的梯度下降,选取当前误分类点使其梯度下降。使用的规则
为 θ := θ −η∇
θ
ℓ(θ),其中 η 是步长,即学习率,∇
θ
ℓ(θ) 是梯度。因此,每次更新权重的公式为:
w ← w + ηyx
b ← b + ηy
我们可以从几何的角度去理解这个更新过程,在此之前,我们可能需要一点点先验知识。
w
⊤
x 是一个内积,在欧几里得空间,点积可以被定义为:
w
⊤
x = |w||x|cos θ
w 是划分直线的法向量,但我们知道直线的法向量是可以有两个方向的,即向左或向右,
那么 w 到底是指哪个方向的法向量呢?从前面的决策函数(即分类规则)可以看出,法向
量 w 指向正类(+1)所在的方向。
为了方便讨论,我们将 w
⊤
x + b 改写为 w
⊤
x,这是完全没有问题的,只需要将 w 和 x
各自增加一个维度即可。这种写法的好处是,我们可以直接从 w 和 x 的内积的符号去判
断分类结果,
如果一个正类的点被误分为负类,即
w
⊤
x
<
0
,那表示
w
和
x
夹角大于
90
度。所以,修正
的方法就是使 w 和 x 夹角小于 90 度,从而让法向量指向该正类点所在的一侧,通常做法是
w ← w + yx, y = 1,如下图所示。根据向量加法的平行四边形法则,一次更新,就可以使得新
的法向量 w + x 与 x 的夹角小于 90 度,这就对该误分类点完成了修正。但是由于学习率的存
在,实际上更新后的法向量为 w + ηx,因此一次更新可能不会让法向量和误分类点的夹角小于
90 度,需要多次更新才能达到目的。
同理,如果一个负类点被误分为正类,即 w
⊤
x > 0,那表示 w 和 x 夹角小于 90 度。修正的方
法就是使 w 和 x 夹角小大于 90 度。通常做法是 w ← w + yx, y = −1 。如下图所示。根据向
量减法的三角形法则,一次更新,就可以使得新的法向量 w − x 与 x 的夹角大于 90 度,这就
对该误分类点完成了修正。同样由于学习率的存在,实际上可能需要多次更新才能达到目的。
63

10.2 参数更新
我们可以证明,当学习率足够小的时候,划分直线与误分类点的距离在参数更新后会变得更小
(这里不在意参数更新后,误分类点是否被正确分类)。这是感知机参数更新的性质,具体证明过
程如下:
对于某个误分类点
−→
x
i
, ˜y
i
, 假设它被选中用于更新参数。
1. 假设迭代之前,分类超平面为 S, 该误分类点距超平面的距离为 d
2. 假设迭代之后,分类超平面为 S
′
, 该误分类点距超平面的距离为 d
′
则:
∆d = d
′
− d =
1
−→
w
′
2
−→
w
′
·
−→
x
i
+ b
′
−
1
∥
−→
w ∥
2
−→
w ·
−→
x
i
+ b
= −
1
−→
w
′
2
˜y
i
−→
w
′
·
−→
x
i
+ b
′
+
1
∥
−→
w ∥
2
˜y
i
−→
w ·
−→
x
i
+ b
≃ −
˜y
i
∥
−→
w ∥
2
−→
w
′
−
−→
w
·
−→
x
i
+
b
′
− b
= −
˜y
i
∥
−→
w ∥
η˜y
i
−→
x
i
·
−→
x
i
+ η˜y
i
= −
˜y
2
i
∥
−→
w ∥
2
η
−→
x
i
·
−→
x
i
+ 1
< 0
因此有 d
′
< d 这里要求
−→
w
′
≃
−→
w , 因此步长 η 要相当小。
具体的感知器参数学习策略如下图所示(摘自邱锡鹏的《神经网络与深度学习》):
图 10.4: 二分类感知器的参数学习算法
在有的文章中(例如周志华的《机器学习》),最后得到的更新公式为:
w ← w + α∆w
b ← b + ∆b
其中,∆w = α(y − ˆy)x,∆b = α(y − ˆy)。
64

10.3 感知器收敛性
这是因为它将样本的类别映射为 0 和 1,同时采取平方和损失函数,所以权值更新的公式不一
样,不过思想都是一样的。这种情况下的更新公式推导可以参考这篇文章《机器学习 _ 感知机》
。
10.3 感知器收敛性
感知机的迭代一定会停下来吗?由感知机算法的定义,可以知道,当找到一条直线,能将平面上
的点都分类正确,那么感知机就会停止。显然,要达到这个终止条件,训练集必须是线性可分的。
如果训练集不是线性可分的,那么上述的感知机算法永远不会停止。
[Noviko, 1963] 证明了对于两类问题,如果训练集是线性可分的,那么感知器算法可以在有限
次迭代后收敛。然而,如果训练集不是线性可分的,那么这个算法则不能确保会收敛。
当数据集是两类线性可分时, 对于训练集 D =
x
(n)
, y
(n)
N
n=1
, 其中 x
(n)
为样本的增广特征向
量, y
(n)
∈ {−1, 1}, 那么存在一个正的常数 γ(γ > 0) 和权重向量 w
∗
, 并且 ∥w
∗
∥ = 1, 对所有 n
都满足 (w
∗
)
⊤
y
(n)
x
(n)
≥ γ. 我们可以证明如下定理.
定理 10.1. 感知器收敛性
给定训练集 D =
x
(n)
, y
(n)
N
n=1
, 令 R 是训练集中最大的特征向量的模,即
R = max
n
x
(n)
如果训练集 D 线性可分,两类感知器的参数学习算法 3.1 的权重更新次数不超过
R
2
γ
2
详细的证明过程参考邱锡鹏的《神经网络与深度学习》第 3.4.2 节(感知器的收敛性)。
10.4 感知机的缺陷
虽然感知器在线性可分的数据上可以保证收敛,但其存在以下不足:
(1)在数据集线性可分时,感知器虽然可以找到一个超平面把两类数据分开,但并不能保证其泛
化能力。
(2)感知器对样本顺序比较敏感.每次迭代的顺序不一致时,找到的分割超平面也往往不一致。
(3)如果训练集不是线性可分的,就永远不会收敛。
65
10.4 感知机的缺陷
66
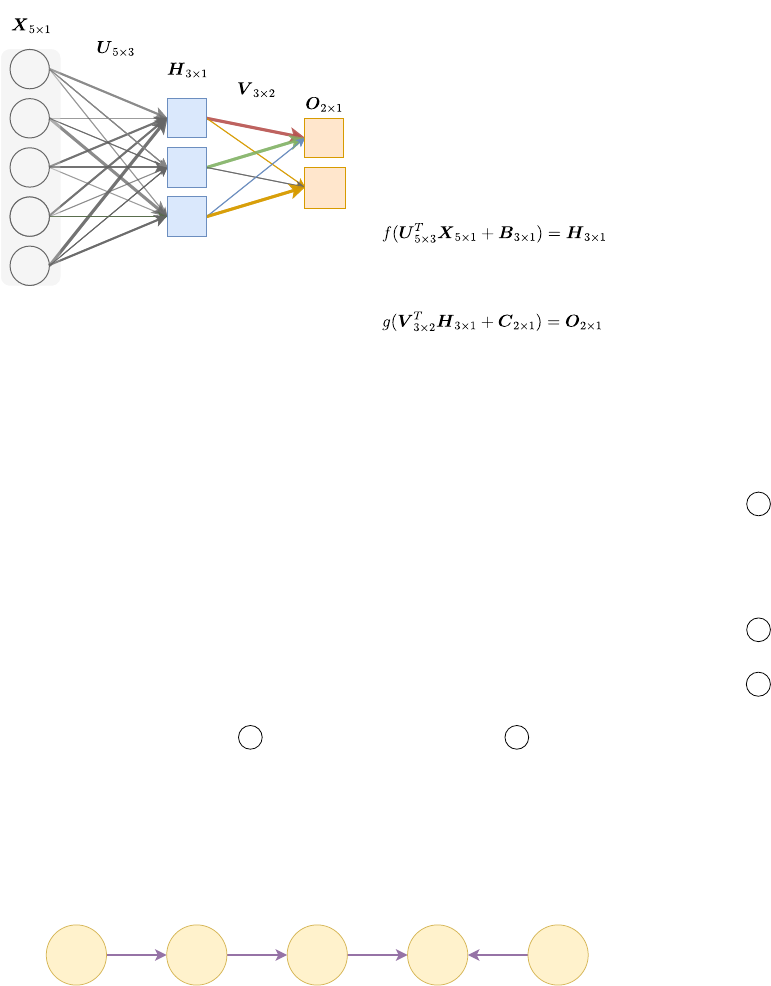
第十一章 Recurrent Neural Networks
11.1 Simple Recurrent Network
11.1.1 前向传播
我们熟悉的神经网络可能是这样的:
input
layer
input→hidden
hidden
layer
output
layer
hidden→output
Description
Uistheweightmatrixfromthe
inputlayertothehiddenlayer
Vistheweightmatrixfromthe
hiddenlayertotheoutputlayer
图 11.1: 三层神经网络示意图
这是一个简单的多层神经网络。它的输入维度是 5,输出维度是 2,隐藏层的维度是 3。用数学
公式表示:
f(U
3×5
X
5×1
+ B
3×1
) = H
3×1
1
其中,f 是隐藏层的激活函数,U 是隐藏层的权重矩阵,B 是隐藏层的偏置向量,当然以下两
种写法在数学上也是等价的:
f(U
T
5×3
X
5×1
+ B
3×1
) = H
3×1
2
f(X
1×5
U
5×3
+ B
1×3
) = H
1×3
3
一般在机器学习的书籍中惯用的写法是 2 。在这里遵循惯例,沿用 2 的写法。那么,从隐藏层
到输出层则表示为:
g(V
T
3×2
H
3×1
+ C
2×1
) = O
2×1
数据在这样的网络中流动(向前传播)的过程是很容易理解和想象的,如果将每一层用一个单元
来表示,可以有更简洁的图例:
X H O
U V
L Y
图 11.2: 三层神经网络简要示意图(包括反向传播过程)
67
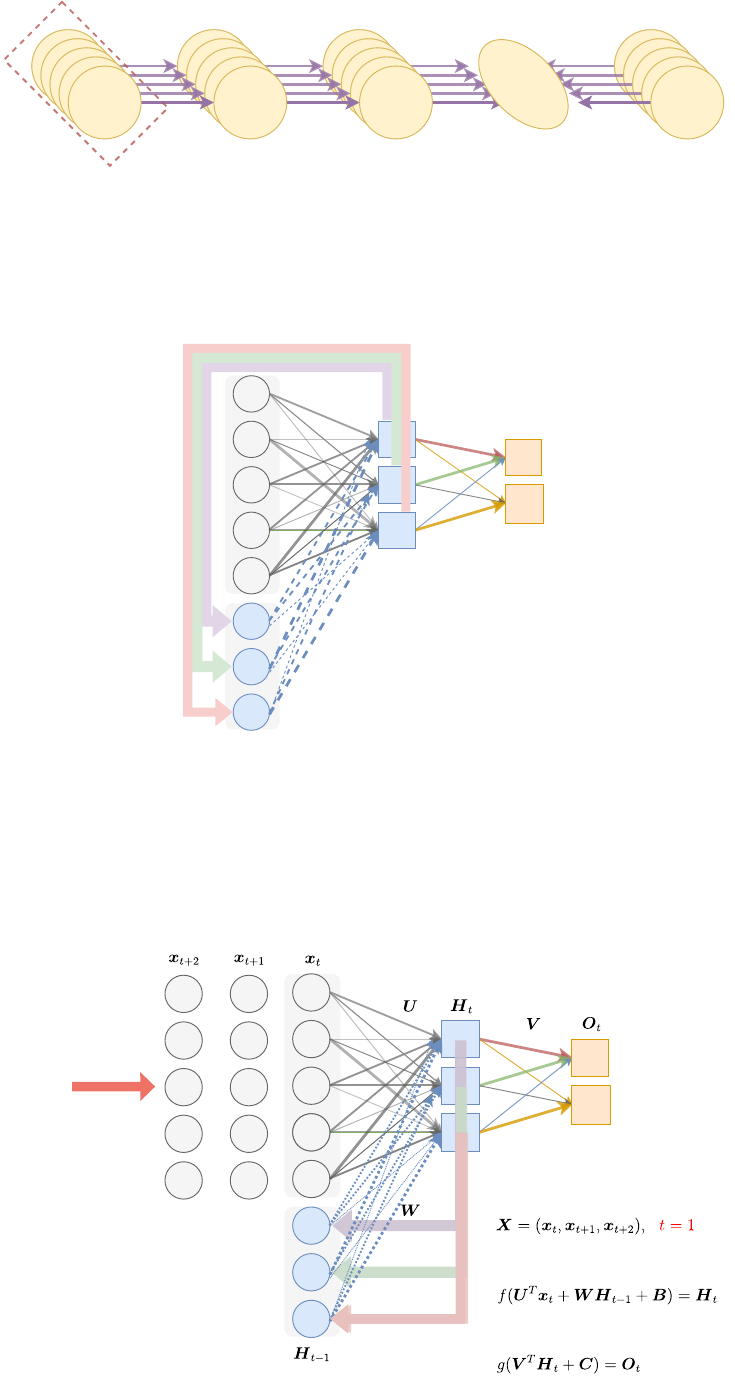
11.1 SIMPLE RECURRENT NETWORK
如果加上 batch size 的话,是这个样子的:
X H O
U V
YX H O
U V
Y
X H O
U V
YX H O
U V
Y
X H O
U V
YX H O
U V
Y
X H O
U V
YX H O
U V
Y
X H O
U V
Y
L
batchsize=5
图 11.3: 三层神经网络简要示意图 (batch size)
与 DNN 不同,Simple RNN 是包含循环结构的网络,几乎没有平面图能很好地展示 Simple RNN
的循环过程,但我尝试画了一张示意图:
图 11.4: Simple RNN 展开示意图
图中,正方形单元存在激活函数,而圆形单元则没有激活函数,因此,圆形单元会将输入值直
接输出,不会对输入的数值作改动。在同一层中,实线和虚线代表着不同的权重矩阵。实际上,
图11.4的输入数据只有一个时间步(time step),这并没有发挥 RNN 的长处。RNN 处理的数据
应该是序列数据,并且具有多个时间步,如图11.5:
68
A
Description
Round units have no activation
functions.
Square units have activation
function.
Wistherecurrentweightmatrixof
thehiddenlayer.
a sample
input → hidden
hidden → output
3timesteps
图 11.5: Simple RNN 展开示意图
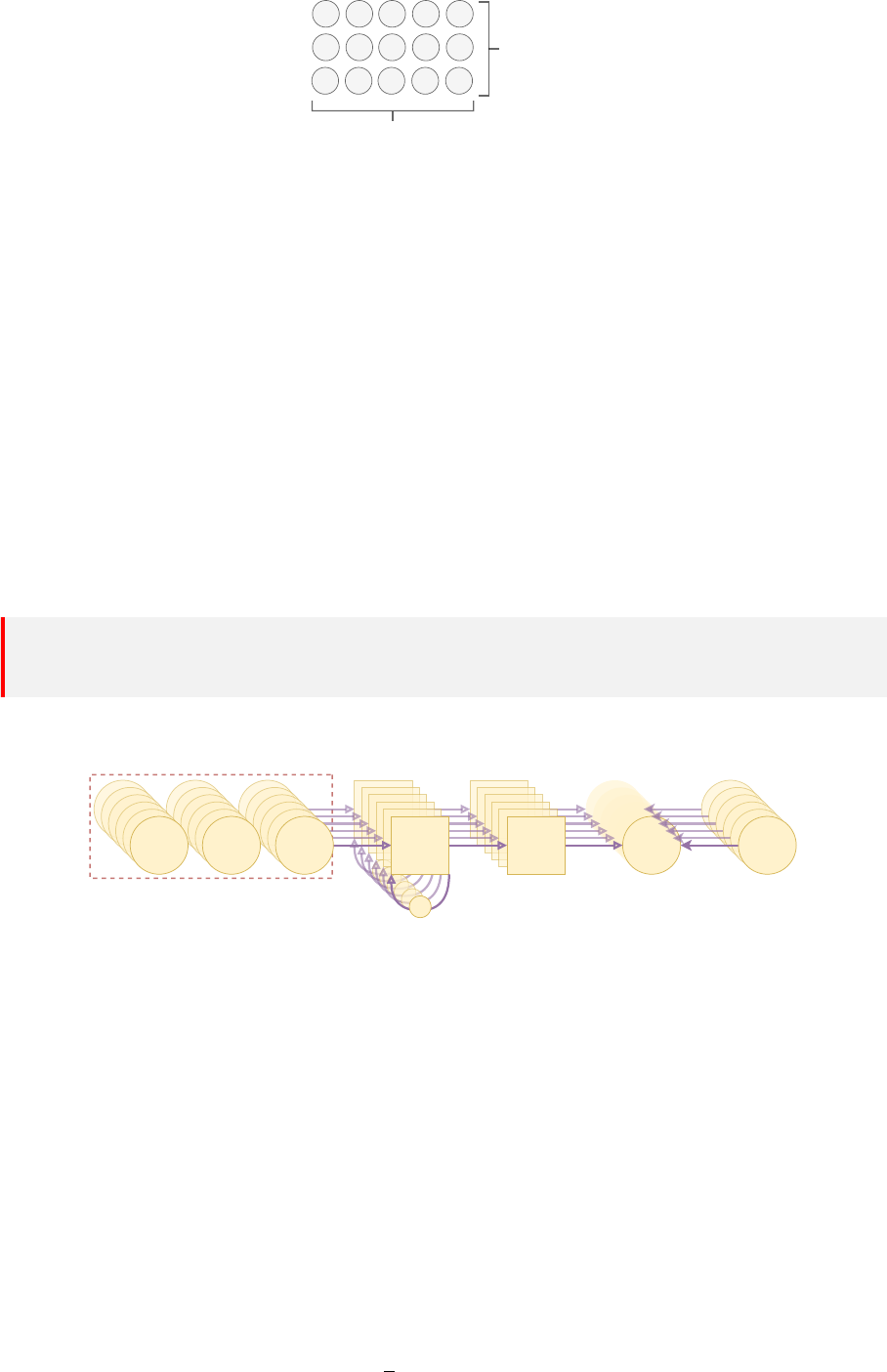
11.1 SIMPLE RECURRENT NETWORK
图11.5中展示的样本数据有 3 个时间步,每一个时间步的数据都是 5 维的,也就是说这个样本
是这样的:
3 time steps
dimensions per time step
各个样本时间步数可能不一样,一般而言,在数据预处理时,我们会将所有样本的时间步处理成
等长的。从图11.5可以看出隐藏层 H
t
不仅由 x
t
决定,也受到 H
t−1
的影响(t 代表第 t 个时
间步),这是 RNN 和 DNN 的不同点,也正是 RNN 循环思想的体现。而 RNN 的输出层 O
t
只
由当前时间步的隐藏层 H
t
决定,这点和 DNN 是一样的。
对于任意 t 时刻,从输入层到隐藏层,用数学公式表示如下:
f(U
T
X + W H
t−1
+ B) = H
t
f(□
T
5×3
□
5×1
+ □
3×3
□
3×1
+ □
3×1
= □
3×1
)
其中,U 是输入层到隐藏层的权重矩阵,W 是隐藏层的循环权重矩阵。隐藏层到输出层的公式
为:
g(V
T
H
t
+ C) = O
t
g(□
T
3×2
□
3×1
+ □
2×1
) = □
2×1
U 、W 和 V 三个权重矩阵和传播过程中是权值共享的。
权值共享是指 U、W 和 V 三个权重矩阵在前向传播的过程中不会改变,不同时间步所使
用的权重矩阵都是一样的。
将 RNN 每一层用一个单元表示,并加上 batch size,可以得到以下图示:
L
X
U V
YH OXX
W
X
U V
YH OXX
W
X
U V
YH OXX
W
X
U V
YH OXX
W
X
U V
YH OXX
W
X
U V
YH OXX
W
batchsize=5
11.1.2 反向传播
与 DNN 一致,RNN 也是通过梯度下降的方法来寻找 U、V、W 这三个参数的最优解,此处我
们考虑较复杂的 Many to Many 形式,损失函数暂定为 MSE 损失函数,由于序列的每个位置都
有损失函数,因此最终损失为:
L =
τ
X
1
L
t
(11.1)
假定我们最终的损失函数为 L,这里假设为 MSE,即:
L =
1
2
output
X
j=1
ˆy
t
j
− y
t
j
2
69
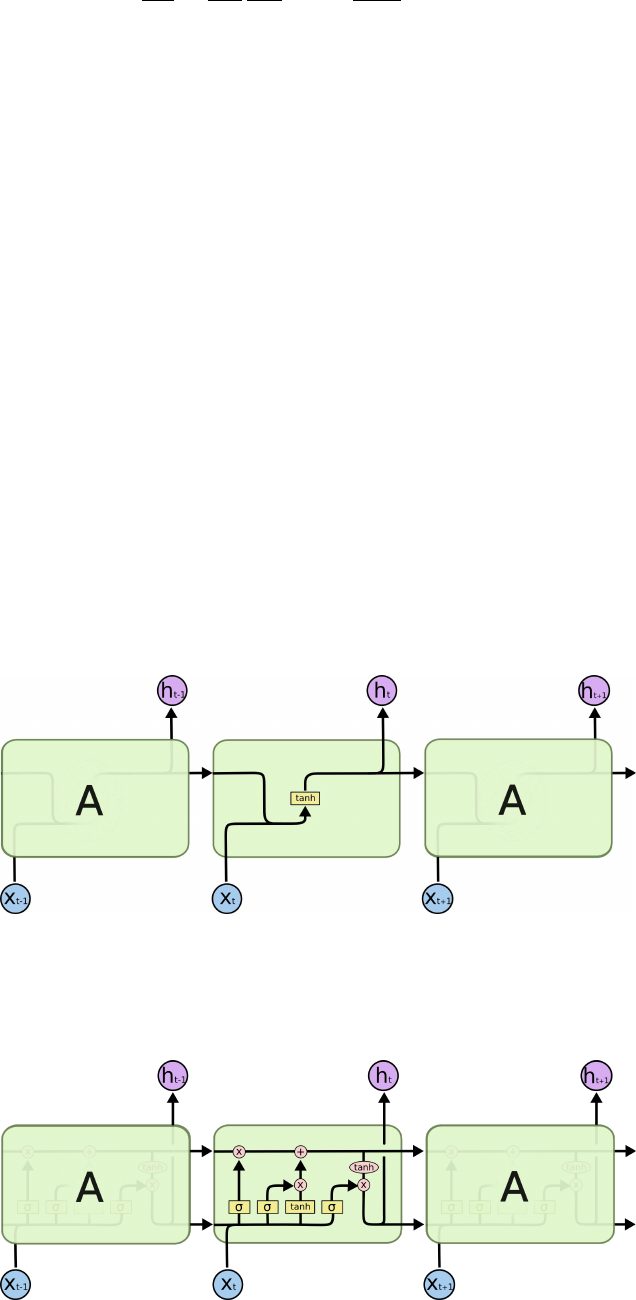
11.2 LSTM
输出层
∂L
∂ ˆy
t
=
∂L
∂L
t
∂L
t
∂ ˆy
t
= 1 ×
∂L
(t)
∂o
(t)
= ˆy
t
− y
t
(11.2)
关于 W
O
和 B
O
的梯度计算如下:
11.1.3 title
11.2 LSTM
11.2.1 LSTM 概述
传统 RNN 模型容易产生梯度消失的问题,难以处理长序列的数据。而造成梯度消失的原因,本
质上是因为隐藏层状态 H
t
的计算方式导致梯度被表示为连乘积的形式,因此 Hochreater 和
Schmidhuber 在 1997 年提出了长短期记忆网络 LSTM,通过精心设计的隐藏层神经元缓解了传
统 RNN 的梯度消失问题。
11.2.2 LSTM 与 RNN 的区别
如果我们略去 RNN 网络的输出层和损失函数,那么模型可以简化为如图11.6的形式(只保留
RNN 的隐藏层),通过线条指示的路径可以清晰地看出隐藏状态 H
t
由 H
t−1
和 x
t
共同决定。
H
t
一方面是 RNN 层当前的输出,另一方面用于计算 H
t+1
图 11.6: RNN 隐藏层
LSTM 和 RNN 区别在于隐藏层的不同。虽然 LSTM 也有这种链状结构,不过其循环结构和
RNN 不同。LSTM 的循环结构中有 4 个神经网络层,并且他们之间的交互非常特别。
图 11.7: LSTM 隐藏层
可以发现,LSTM 和 RNN 的隐藏层都只有一个输出,就是 H
t
,并且 H
t
都参与了下一时刻的
前向传播。但除了 H
t
,LSTM 还有一个隐藏状态也参与了前向传播,但这个隐藏状态没有被输
70
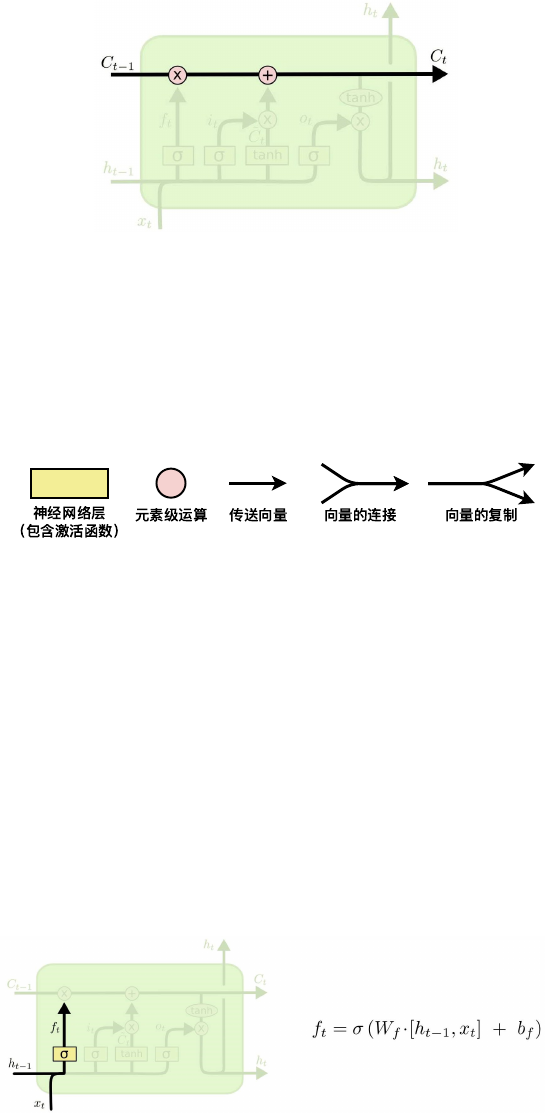
11.2 LSTM
出。我们称这个隐藏状态为细胞状态 C
t
(Cell State)。C
t
在 LSTM 中实质上起到了 RNN 中隐
藏状态 H
t
的作用。
除了 H
t
和细胞状态 C
t
,图中还有三个结构,这些结构一般称之为门控结构 (Gate)。LSTM 的
门控结构一般包括遗忘门,输入门和输出门三种,这三个门结构都是用来控制 C
t
的状态。
图 11.8: cell state
LSTM 的关键是细胞状态 C
t
,C
t
横穿整个 LSTM 单元顶部的水平线。LSTM 通过门结构对细
胞状态添加或者删除信息。门是一种选择性让信息通过的方法。它们由一个 Sigmoid 神经网络
层和一个元素级相乘操作组成。
在开始之介绍 LSTM 各个门结构前,我们先介绍一下将用到的标记。
在上图中,每条线表示向量的传递,从一个结点的输出传递到另外结点的输入。粉红圆表示向量
的元素级操作,比如相加或者相乘。黄色方框表示神经网络的层。线合并表示向量的连接,线分
叉表示向量复制。接下来按运算顺序介绍 LSTM 的三个门结构。
11.2.3 遗忘门
LSTM 的第一步是决定我们将要从细胞状态中扔掉哪些信息。该决定由一个叫做“遗忘门 (For-
get Gate)”的 Sigmoid 层控制。H
t−1
和 x
t
被输入遗忘门,经过 Sigmoid 激活函数,输出一个
向量 f
t
,f
t
的元素与 C
t−1
的元素一一对应,并且 f
t
的元素都是 0 ∼ 1 之间的数,1 表示“完
全保留该信息”,0 表示“完全丢弃该信息”。即遗忘门以一定的概率控制是否遗忘上一个时刻的
细胞状态。
f
t
= σ (W
f
h
t−1
+ U
f
x
t
+ b
f
) (11.3)
11.2.4 输入门
第二步是决定我们将会把哪些新信息存储到元胞状态中。这步分为两部分:
• 首先,有一个叫做“输入门 (Input Gate)”的 Sigmoid 层决定我们要更新哪些信息。
71
11.3 带窥孔的 LSTM
• 接下来,一个 tanh 层创造了一个新的候选值
˜
C
t
,该值可能被加入到元胞状态中。
在第三步中,LSTM 把这两个值组合起来用于更新元胞状态。
i
t
= σ (W
i
h
t−1
+ U
i
x
t
+ b
i
) (11.4)
˜
C
t
= tanh (W
C
h
t−1
+ U
C
x
t
+ b
C
) (11.5)
11.2.5 细胞状态更新
现在我们该将旧细胞状态 C
t−1
更新到新状态 C
t
了。上面的步骤中已经决定了该怎么做,这一
步我们只需要实际执行即可。
C
t
= C
t−1
⊙ f
t
+ i
t
⊙
˜
C
t
(11.6)
⊙ 是矩阵的 Hadamard 积 (两个矩阵相同位置元素的乘积)。新状态即为旧状态乘以需要忘记的
概率,加上新的候选值乘以需要更新的比率。
11.2.6 输出门
最后,我们需要决定最终的输出。输出将会基于目前的细胞状态,并且会加入一些过滤。首先我
们建立一个 Sigmoid 层的输出门 (Output Gate),来决定我们将输出元胞的哪些部分。然后我们
将元胞状态通过 tanh 之后(使得输出值在-1 到 1 之间),与输出门相乘,这样我们只会输出我
们想输出的部分。
o
t
= σ (W
o
h
t−1
+ U
o
x
t
+ b
o
) (11.7)
h
t
= o
t
⊙ tanh
˜
C
t
(11.8)
11.3 带窥孔的 LSTM
本文前面所介绍的 LSTM 是最普通的 LSTM,但并非所有的 LSTM 模型都与前面相同。事实
上,似乎每一篇 paper 中所用到的 LSTM 都是稍微不一样的版本。不同之处很微小,不过其中
一些值得介绍。
一个流行的 LSTM 变种,由 Gers & Schmidhuber (2000) 提出,加入了“窥视孔连接 (peephole
connection)”。也就是说我们让各种门可以观察到元胞状态。
11.4 GRU
另一个变化更大一些的 LSTM 变种叫做 Gated Recurrent Unit,或者 GRU,由 Cho, et al. (2014)
提出。GRU 将遗忘门和输入门合并成为单一的“更新门 (Update Gate)”。GRU 同时也将元胞
状态 (Cell State) 和隐状态 (Hidden State) 合并,同时引入其他的一些变化。该模型比标准的
LSTM 模型更加简化,同时现在也变得越来越流行。
图中,r
t
是 GRU 模型的重置门部分,用于控制前一时刻隐藏状态 h
t−1
对当前状态的影响。若
h
t−1
不重要,从语言模型角度看,即从当前开始表达新的意思,与上文无关,则重置门关闭,数
学表达式为:
r
t
= σ (W
r
h
t−1
+ U
r
x
t
+ b
r
) (11.9)
72
11.4 GRU
图中 z
t
是 GRU 模型的更新门部分,用于决定是否忽略当前输入 x
t
,类似 LSTM 中的输入门
i
t
。从语言模型角度看,即判断当前词 x
t
对整体意思的表达是否重要,数学表达式为:
z
t
= σ (W
z
h
t−1
+ U
z
x
t
+ b
z
) (11.10)
定义完 GRU 的重置门和更新门之后,我们再来看 GRU 的细胞更新。当更新门打开时,h
t
由
h
t−1
和 x
t
决定;当更新门被关闭时,h
t−1
将仅由 h
t−1
决定,帮助梯度反向传播,与 LSTM 相
同,这种机制有效地缓解了梯度消失现象。数学表达式为:
˜
h
t
= tanh (W r
t
⊙ h
t−1
+ Ux
t
+ b
f
) (11.11)
h
t
= (1 − z
t
) ⊙ h
t−1
+ z
t
⊙
˜
h
t
(11.12)
73
11.4 GRU
74
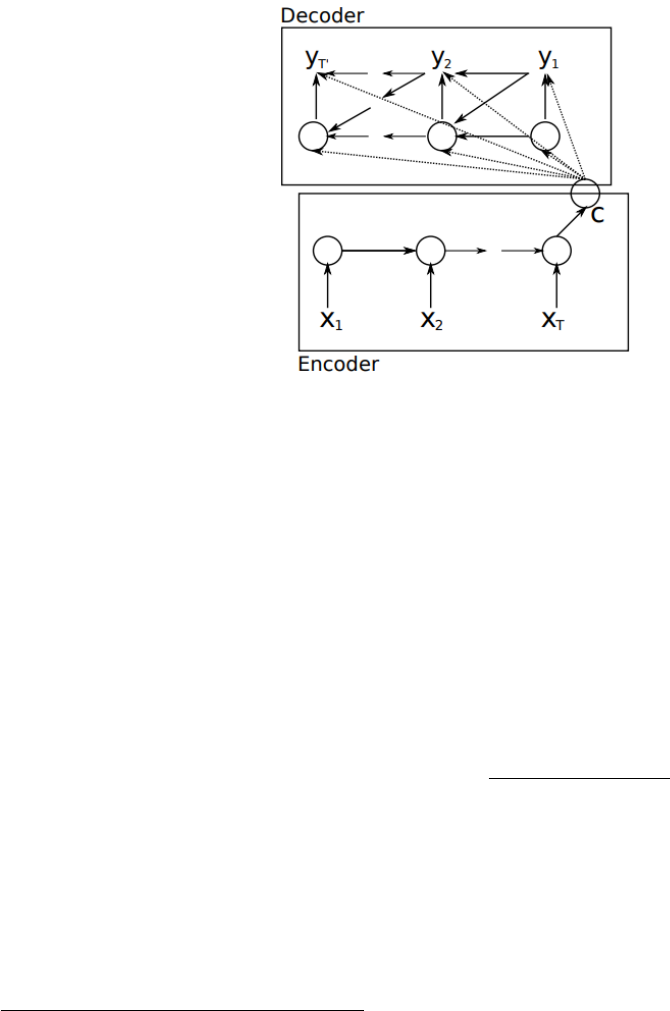
第十二章 Seq2Seq
12.1 Encoder-Decoder
Kyunghyun Cho 等人在 2014 年 6 月 3 日将论文《Learning Phrase Representations using RNN
Encoder–Decoder for Statistical Machine Translation》发布于 Arxiv,提出了 Encoder–Decoder
模型结构。论文提出的 RNN Encoder-Decoder 模型由两个 RNN 组成:
简要地回顾 RNN 的知识:
RNN 是一个包含隐藏状态 h 和可选输出 y 的神经网络,它接受可变长序列 x = (x
1
, . . . , x
T
) 的
输入。在每个时间步,隐藏状态 h
⟨t⟩
按照如下公式更新:
h
⟨t⟩
= f
h
⟨t−1⟩
, x
t
其中 f 是非线性激活函数。f 可以像 logistic、sigmoid function 一样简单,也可以像 long short-
term memory(LSTM)一样复杂。
以输入序列的下一个字符作为预测目标来训练,RNN 可以学习序列上的概率分布
1
。在这种情况
下,每个时间步长 t 的输出是条件分布 p (x
t
|x
t−1
, . . . , x
1
)。例如,对于所有 j = 1, ··· , K,可以
使用 softmax 激活函数输出多项式分布(1-K 编码)
p (x
t,j
= 1|x
t−1
, . . . , x
1
) =
exp
w
j
h
⟨t⟩
P
K
j
′
=1
exp
w
j
′
h
⟨t⟩
(12.1)
其中 w
j
是权重矩阵 W 的行。通过组合这些概率,我们可以用如下公式计算序列 x 的概率:
p(x) =
T
Y
t=1
p (x
t
|x
t−1
, . . . , x
1
) (12.2)
从这个学习的分布中,通过在每个时间步长迭代采样符号来直接抽样新序列。
1
此时,RNN 的拟合目标就是这个概率分布。
75
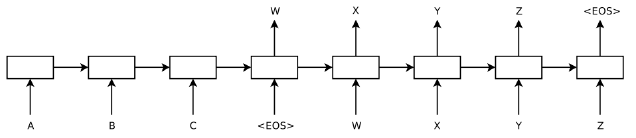
12.2 SEQ2SEQ
RNN Encoder-Decoder 模型:
Encoder 将输入序列 X 编码为一个固定长度的向量 c,Decoder 将输入的固定长度向量 c 解码
成输出序列 Y 。从概率的角度来看,这种结构是一种通用方法,可学习一个可变长序列在另一
个可变长序列下的条件分布:p (y
1
, . . . , y
T
′
|x
1
, . . . , x
T
),值得注意的是代表了输入序列长度的 T
和输出序列长度 T
′
可以不一样。
编码器是一个 RNN,依次读取输入序列 x 的每个字符。当它读取每个字符时,RNN 的隐层状
态会根据公式(1)改变。当读到序列的结尾(由 end-of-sequence 符号标记)后,RNN 隐层状
态 c 包含了整个输入序列的信息。
模型的解码器是另一个 RNN,通过给定隐藏状态 h
⟨t⟩
和下一个输出字符 y
t
,解码器被训练输出
序列。然而,与上述的 RNN 不同,y
t
和 h
t
都受制于 y
t−1
和 Encoder 隐藏状态 c。因此,在 t
时刻解码器的隐藏状态是由下述公式计算:
h
⟨t⟩
= f
h
⟨t−1⟩
, y
t−1
, c
(12.3)
类似的,下一个 symbol 的条件分布为:
P (y
t
|y
t−1
, y
t−2
, . . . , y
1
, c) = g
h
(t)
, y
t−1
, c
(12.4)
f 与 g 为激活函数,g 必须能生成有效的概率,比如利用 softmax。
12.2 Seq2Seq
正式提出 Sequence to Sequence 的文章是《Sequence to Sequence Learning with Neural Net-
works》。Sequence to Sequence 的意思是:输入一个序列,输出另一个序列。Seq2Seq 一词
带有歧义,在原论文中,Seq2Seq 指代输入和输出都是序列的机器学习任务,但现在很多人都
将 Seq2Seq 视作一种模型,或者特指原文论中的模型。在我看来,Seq2Seq 更准确的含义是序
列学习任务,而不是作为模型的概念。即使 Seq2Seq 指代模型,也应该是一类模型(输入和输
出都是序列的模型),而不是一种模型。之所以强调 Seq2Seq 的含义,是因为 Seq2Seq 往往和
Encoder-Decoder 有关,如果模糊 Seq2Seq 的含义,Seq2Seq 和 Encoder-Decoder 两者同时出现
容易让人感到混乱。
这篇论文提出了如下图结构的模型(<EOS> 是句子结束的标识符):
实际上,这就是一个 Encoder-Decoder 结构的模型,但是它比 RNN Encoder-Decoder 模型简
单一些。因为 Decoder 在 t 时刻是由 h
t
和 y
t−1
计算出 y
t
,而没有 c。论文中的 Encoder 和
Decoder 都是用 4 层 LSTM。
LSTM 的目标是估计条件概率 p (y
1
, . . . , y
T
′
|x
1
, . . . , x
T
) ,其中 (x
1
, . . . , x
T
) 是输入序列,y
1
, . . . , y
T
′
是对应的输出序列。模型先获得输入序列 (x
1
, . . . , x
T
) 的固定维度的向量表示 v,v 是 Encoder
的最后一个隐藏状态,同时也是 Decoder 的初始隐藏状态。然后模型通过标准的 LSTM 计算公
式计算出 y
1
, . . . , y
T
′
的条件概率:
p (y
1
, . . . , y
T
′
|x
1
, . . . , x
T
) =
T
′
Y
t=1
p (y
t
|v, y
1
, . . . , y
t−1
)
76
12.3 ATTENTION 机制
12.3 Attention 机制
Attention 机制由视觉图像领域提出来,在 2014 年,Bahdanau 在《Neural Machine Translation
by Jointly Learning to Align and Translate》上将其应用到机器翻译任务上,这是第一个应用到
NLP 领域的论文。之后,15、16、17 乃至今年,都有各式各样的 attention 机制结合深度学习网络
模型被用于处理各种
NLP
的任务。在
2017
年,
google
机器翻译团队发表的《
Attention is all you
need》中大量使用了自注意力机制(self-attention)来学习文本表示,脱离传统的 RNN/CNN,
同时也使用了新颖的 multi-head 机制。自注意力机制也成为了大家近期研究的热点,可以应用
到各种 NLP 任务上。
Attention 机制经过长时间的发展,虽然不同论文里的实现方法可能各不一样,但是基本上都遵
循着同一个范式。其中包含三个成分:
Key(键) 与值相对应同时又用来与查询计算相似度作为 Attention 选取的依据
Query(查询) 一次执行 Attention 时的查询
Value(值) 被注意并选取的数据
对应的公式为:
Attention (K, Q, V ) = softmax(Similarity(K, Q))V (12.5)
可以看出 attention 的计算分为三步:
计算 K、Q 的相似矩阵
对相似矩阵作归一化处理
其中,相似矩阵的计算有很多种方式:
77

