高等代数
siwing
2022 年 2 月 27 日
2
目录
第一部分 线性代数初步 1
第一章 基本概念 3
1.1 集合 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
1.2 映射与变换 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
1.3 代数运算 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
1.4 运算律 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
第二章 线性方程组 11
2.1 高斯消元法 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11
2.2 解的情况及其判别准则 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15
2.3 快速消元法与行列式的递归定义 . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15
2.3.1 二阶和三阶行列式 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16
2.3.2 四阶行列式 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
2.3.3 归纳证明 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20
2.4 Cramer 法则 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
2.5 后话——Laplace 公式与平行多面体有向体积 . . . . . . . . . . . . . . . . . . . . 23
第三章 行列式 25
3.1 斜对称多线性函数与行列式的界定定理 . . . . . . . . . . . . . . . . . . . . . . . . 25
3.2 行列式的几何意义——Leibniz formula . . . . . . . . . . . . . . . . . . . . . . . . 27
3.3 标量面积 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29
3.4 行列式的逆序式定义 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30
3.4.1 排列与逆序数 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31
3.4.2 n 阶行列式的逆序数定义 . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32
3.5 对比行列式的三种定义 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33
3.6 行与列的对称地位 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33
3.7 行列式的性质 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35
3.7.1 行列式展开式的角度 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35
3.7.2 几何体积的角度 [wx] . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 37
3.8 行列式按一行 (列) 展开 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 43
3.9 拉普拉斯定理 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 46
3
目录
3.9.1 范德蒙行列式 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 48
第四章 向量空间 51
4.1 n 维向量 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 51
4.2 线性相关 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 52
4.3 极大线性无关组 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 55
4.4 线性相关与线性方程组的有解判别 . . . . . . . . . . . . . . . . . . . . . . . . . . 59
第五章 矩阵初步 61
5.1 矩阵的秩 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 61
5.2 线性方程组有解判别定理 (下) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 65
5.3 矩阵的运算 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 66
5.4
矩阵乘积的行列式与秩
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 69
5.5 矩阵的逆 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 72
5.5.1 逆矩阵与线性方程求解 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 74
5.6 矩阵的分块乘法 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 75
5.7 初等矩阵 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 77
第六章 线性空间 81
6.1 线性空间的定义 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 81
6.2 线性空间的简单性质 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 83
6.3 向量加法交换律的 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 84
6.4 维数、基、坐标 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 84
6.5 基变换与坐标变换 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 85
6.5.1 基变换解释 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 86
6.6 线性子空间 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 87
6.7 子空间的交与和 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 88
6.8 子空间的直和 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 91
6.9 线性空间的同构 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 93
第七章 线性变换 97
7.1 平面上基本的线性变换 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 97
7.1.1 旋转变换 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 97
7.1.2 镜射变换 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 97
7.1.3 伸缩变换 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 98
7.1.4 推移变换 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 98
7.1.5 线性变换的表示与矩阵乘法的诞生 . . . . . . . . . . . . . . . . . . . . . . 99
7.1.6 线性变换的分解 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 100
7.2 线性映射的定义与性质 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 100
4
7.3 线性映射的运算 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 102
7.4 线性映射和线性变换的矩阵表示 . . . . . . . . . . . . . . . . . . . . . . . . . . . . 105
第八章 附录 111
8.1 附录 I 线性代数的含义 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 111
8.2 附录 II 名词解释 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 112
8.3 附录 III 代数结构 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 115
8.4 附录 IV 空间 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 118
8.5 附录 V 补充证明 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 120
第一部分
线性代数初步
1

第一章 基本概念
1.1 集合
一个集合是我们的感官或思维所能辨识、确认的事物聚集而成的整体,这些事物称
为该集合的元素。
———康托尔
集合论是近现代数学的基石,很多数学概念的精确定义都有赖于集合论。当集合论的创始者康
托发表他大胆的新观念与论述时,只有少数的数学家认识到它的重要性。但当它逐渐发展,集合
的理论几乎渗透了数学的所有领域,并对它们的发展产生广泛的影响,甚至还改变了原有定理的
形貌。事实上,在某些数学领域,如拓扑的发展本质上完全仰赖于集合论的方法。如今,集合论
的语言已成为全世界数学家所共认及引述的用语。集合论显示了一种统合的力量,赋予数学各
个分支一个共通的基底,并使它们的概念达到相当清晰且明确的境界。
在通俗的用法中,正如康托尔所说,集合表示一些不同的事物的聚合,且从某种观点来看,这些
事物属于同一族类或相似。事实上,这个定义缺乏精确,并会导致一些悖论
1
,这直接导致了第
三次数学危机
2
,并促使了近代公理集合论的兴起和发展。最早的公理化工作由德国数学家策梅
洛 (Zermelo) 所承担,他于 1908 年建立他的集合论公理系统。后经弗兰克尔 (Frankel)、冯诺伊
曼
(Von Neuman)
和斯科伦
(Skolem)
等人的凡次改进,终于形成了著名的
ZFC
系统。
ZFC
系
统避免了历史上已被发现的悖论,而且至今未被发现有新的悖论。不幸的是,哥德尔第二不完备
定理表明:ZFC 的相容性不能在 ZFC 自身之内证明。因为 ZFC 的延展包括了通常意义上的大
部分数学,所以 ZFC 的相容性也不能在其他数学分支中证明,但 ZFC 的相容性可从弱不可达
基数的存在
3
(独立于 ZFC) 而得出。虽然 ZFC 无法自证相容性,但是几乎没有人怀疑 ZFC 有
什么未被发觉的矛盾。人们普遍相信如果 ZFC 有什么未被发觉的矛盾早就该被发掘出来了。
如今,人们称康托尔所创建的集合论为古典集合论,又因康托尔只以朴素的形式陈述他的理论,
通常又叫做朴素集合论。虽然朴素集合论存在一些矛盾,但它已足以用于引介许多重要的数学
定义与概念。因此,本节只叙述一些集合论中朴素意义下的必要概念。
康托尔创建古典集合论的最重要的思想方法就是概括原则:任给一个一元谓词,即性质 p,则就
能把所有具有性质 p 的对象,也仅由这些具有性质 p 的对象 x 汇集起来构成一个集合。用符号
来表达就是
A = {a | p(x) } 或 x ∈ A ↔ p(x)
通常使用大写字母 A, B, C, . . . 来表示集合,用小写字母 a, b, c, . . . 来表示集合的元素。记 A 为
一个集合,如果 a 是 A 中的元 素,则称 a 属于 A,记为 a ∈ A,否则记为 a /∈ A。我们也可以
将集合 A 表示为 A = {a | a ∈ A},其中 a ∈ A 可以用 A 中元素满足的共同性质代替,比如说
偶数集合 = {a 为整数 | a ≡ 0 mod 2}。注意到集合中元素总是不重复的。
定义1.1 子集: 如果集合 A 中的每一个元素均是集合 B 中元素,则称 A 是 B 的子集 (subset),
换言之,即若 a ∈ A,则 a ∈ B。此时我们记为 A ⊆ B 或 B ⊇ A。
1
罗素悖论、布拉利-福尔蒂悖论和康托尔悖论。
2
虽然第二、三次危机确实存在,但第一次危机并无史实依据,而是后人推测和编造的。
3
ZFC 系统无法证明弱不可达基数的存在。
3
1.1 集合
定义1.2 相等: 如果集合 A ⊆ B 且 B ⊆ A,即 a ∈ A 当且仅当 a ∈ B,称 A 与 B 相等,并记
为 A = B。
定义1.3 真子集: 如果 A ⊆ B 且 A 6= B,我们称 A 为 B 的真子集 (proper subset),记为 A ⊂ B
或者 A ⊊ B。
定义1.4 空集: 不含任何元素的集合称为空集 (empty set),记为 ∅。空集 ∅ 被认为是任何集合
的子集,且是任何非空集合的真子集。注意到,空集是唯一被定义的集合。后来的发展证实了引
入空集在整化集合的论证上颇具效用。
常用的集合符号有:N 自然数集,Z 整数集,Z
∗
非零整数集;Q 有理数集,Q
∗
非零有理数集。
定义1.5 有限集、无限集: 如果集合 A 的元素个数有限,称 A 为有限集 (nite set),其元素个
数称为集合的阶 (cardinality 或 order of nite set),记为 |A|。元素个数无限的集合,即无限集
(innite set),它的阶定义为 ∞。
定义1.6 族、系: 元素本身为集合的集合称为族或系。有一个很重要的族是一个已知集 S 的所
有子集的集合,它称为 S 的幂集合,记为 P (S)。
我们已熟知,互异的实数 a, b 存在大小关系,即 a < b 或 b < a。若 a < b,我们也可以说,对
于数对 (a, b) 而言,关系 < 成立。从另一种观点来看,这个关系可以用所有满足该关系的序数
对的集合来表示。这个想法引导我们有了如下定义:
定义1.7 关系(二元关系): 集合 S 中的二元关系 R 是指 S 中元素所成序对的某种集合。若
(a, b) ∈ R,我们也说 (a, b) 满足关系 R,有时我们也写为 aRb。
上面的定义中,序对一词是按直观的意义引用,意指两物 a 与 b 的聚合,但 a 是为此聚合中的
第一元素,b 为第二个。
定义1.8 定义域与值域: 设 R 是 S 中的一个二元关系,由 (x, y) ∈ R 所确定的所有 x 组成的集
合称为 R 的定义域或前域,记为 dom R(the domain of R),dom R = {x|∃y ∈ S, (x, y) ∈ R}。相
似的,对于 x ∈ S,使得 (x, y) ∈ R 的所有 y 组成的集合称为 R 的值域或后域,记为 ran R(the
range of R),ran R = {y|∃x ∈ S, (x, y) ∈ R}。R 的定义域和值域的并集称为 R 的变域或全域,
记为 FLD(R)(the eld of R),FLD(R) = dom R
S
ran R。显然,FLD(R) ⊆ S。
不同的关系可以有不同的性质,下面列出了比较重要的一些性质,其中 R 表示 S 中的关系。
• R 具有反身性:对所有 x ∈ S,xRx 成立。
• R 具有对称性:若 xRy 则 yRx 成立。
• R 具有非对称性:S 中没有元素 x, y 可使 xRy 和 yRx 同时成立。
• R 具有反对称性:若 S 中的元素 x, y 同时满足 xRy 和 yRx,则 x = y。
• R 具有传递性:若 xRy 且 yRz,则 xRz。
• R 具有连通性:若 x 6= y,则 xRy 或 yRx。
• R 具有左唯一性:若 xRz 且 yRz,则 x = y。
• R 具有右唯一性:若 xRy 且 xRz,则 y = z。
• R 具有双唯一性:。R 同时具有左唯一性和右唯一性。
一个很常见的关系是等价,等价关系不但在数学的每个角落里都可以找到,甚至在所有科学里均
可见其踪迹。
定义1.9 等价关系 (equivalent): 等价描述同类物件之间的关系,若集合 S 中的关系具有以下
三个性质,且其前域为 S,则称此关系为等价关系。
1. 反身性:x 等价于 x;
2. 对称性:若 x 等价于 y,则 y 等价于 x;
3. 传递性:若 x 等价于 y 且 y 等价于 z,则 x 等价于 z。
4
1.2 映射与变换
若物件 x 等价于 y,那么 x 和 y 必定存在某种定义明确的关系,而且经由某种运算可以将 x 变
换为 y,也可以将 y 变换回 x。
1.2 映射与变换
定义1.10 映射: 设 X 与 Y 是两个集合,所谓集合 X 到集合 Y 的一个映射就是指一个法则 φ,
它使 X 中每一个元素 x 都有 Y 中一个确定的元素 y 与之对应。映射常写成
φ : X 7−→ Y 或 y = φ(x)
其中,y 称为 x 在映射 φ 下的像,而 x 称为 y 在映射 φ 下的一个原像(或逆像)。
由定义可以看出,集合 X 到集合 Y 的一个法则 φ,在满足以下三个条件时才是一个映射:
1. φ 对于 X 中每个元素都必须有象;
2. X 中相等元素的象也必须相等,亦即 X 中每个元素的象是唯一的;
3. X 中每个元素的象必须属于 Y 。
映射是通常函数概念的一种推广,集合 X 相当于定义域。不过应注意,集合 Y 包含值域,但不
一定是值域。就是说,在映射 φ 之下不一定 Y 中每个元素都有原象。注意,多值函数虽然有多
个值,但也是一个映射,因为映射并不要求一定映射到实数域,也可以映射到数对 R
n
。
定义1.11 满射 (onto; surjective): 设 φ 是集合 X 到 Y 的一个映射,我们用 φ(X) 代表 X
在映射 φ 下像的全体,称为 X 在映射 φ 下的像集合。显然
φ(X) ⊂ Y
如果 φ( X) = Y ,映射 φ 就称为映上的
4
或满射。换而言之,满射意味着在 φ 之下,Y 的每个元
素在 X 中都有原像。
定义1.12 单射 (one-to-one; injective): 如果在映射 φ 下,X 中不同元素的像也一定不同,即
由 x
1
6= x
2
一定有 φ (x
1
) 6= φ (x
2
),那么映射 φ 就称为 X 到 Y 的一个单射,或 X 到 Y 里 的
一一映射。
定义1.13 双射 (one-to-one correspondence; bijective): 一个映射如果既是单射又是满射
就称为 1 − 1 对应或双射。
非映射 非映射
单射但非满射
满射但非单射 双射 非单射亦非满射
图 1.1: 不同映射辨识
定义1.14 相等的映射: 集合 X 到集合 Y 的两个映射 φ 及 τ,若对 X 的每个元素 x 都有
φ(x) = τ(x),则称它们相等,记作 φ = τ 。
4
φ : X 7−→ Y 且 φ 是映上的意味着 φ 是 X 到 Y 上 的一个映射。
5

1.3 代数运算
定义1.15 映射乘法/复合映射: 设 φ, τ 分别是集合 X 到 Y 、Y 到 M 的映射,乘积 τ φ 定义为
(τφ)(x) = τ (φ(x)), x ∈ X
即相继施行 φ 和 τ 的结果, τ σ 是 X 到 M 的一个映射。
映射的乘法具有结合律,设 φ, τ, ψ 分别是集合 M 到 M
′
、M
′
到 M
′′
、M
′′
到 M
′′′
的映射,映
射乘法的结合律为
(ψτ )φ = ψ(τφ)
证明. 等式两端显然都是 M 到 M
′′′
的映射,要证明它们相等,只需要证明它们对于 M 中每个
元素的作用都相同,即
(ψτ )φ(a) = ψ(τ φ)(a), 对每个a ∈ M
由定义
(ψτ )φ(a) = (ψτ )(φ(a)) = ψ(τ (φ(a)))
ψ(τ φ)(a) = ψ((τ φ)(a))) = ψ( τ (φ(a)))
这就证明了映射的结合律。
不难证明,两个双射映射的乘积也是一个双射。根据映射乘法的定义,容易看出,映射并不满足
交换律。这告诉我们一个事实:结合律是更一般的规律。
定义1.16 恒等映射: 设 M 是一集合,定义
σ(a) = a, a ∈ M
即 σ 把每个元素映到它自身,称为集合 M 的恒等映射或单位映射,记为 1
M
。在不致引起混淆
时,也可以简单地记为 1。
定义1.17 逆映射: 对于 X 到 Y 的双射 φ 我们可以自然地定义它的逆映射,记为 φ
−1
。因为 φ
是满射,所以 Y 中每个元素都有原像,又因为 φ 是单射,所以 Y 中每个元素只有一个原像,我
们定义
φ
−1
(y) = x, 当φ(x) = y, x ∈ X, y ∈ Y
显然,φ
−1
是 Y 到 X 的一个双射,并且
σ
−1
σ = 1
X
, σσ
−1
= 1
Y
定义1.18 变换: M 到 M 自身的映射,有时也称为 M 到自身的变换。
同样可定义满射变换、单射变换和双射变换,恒等映射显然也是一个恒等变换。
1.3 代数运算
抽象代数的主要任务是研究各种抽象的代数系统(代数结构),所谓代数结构是指带有运算的集
合。现在我们要严格指出,所谓“带有运算”究竟是什么意思。
定义1.19 代数运算: 设 M 是一个集合,如果有一个法则,它对 M 中任意两个有次序的元素 a
与 b,在 M 中都有一个唯一确定的元素 d 与它们对应,则称这个法则是集合 M 的一个代数运
算。
如果我们用记号
◦
表示这个代数运算,则平常把
a
与
b
通过
◦
所确定的元素
d
记为
a ◦ b = d
6
1.4 运算律
就是说,对 M 中任二元素 a, b,通过所规定的法则 ◦,“算”出一个元素 d 来,而 d 必须属于
M。这正是通常的加法和乘法运算所共有的最本质的属性。因此,代数运算就是通常加法和乘法
运算在最一般情况下的一种自然推广。
设 M 是一个集合,用 T (M ) 表示 M 的全体变换作成的集合。任取 σ, τ ∈ T (M),则对 M 中
任意元素 x,规定
στ (x) = σ(τ(x))
显然 στ 也是 M 的一个变换,即 στ ∈ T (M)。我们称此法则为变 换的乘法,它是 T (M) 的一
个代数运算,并把 στ 叫做变换 σ 与 τ 的乘积。
若用 ε 表示集合 M 的恒等变换,则对任意 σ ∈ T (M) 都有
σε(x) = εσ(x) = σ(x), x ∈ M
从而
εσ = σε = σ
即在变换的乘法中, 恒等变换起着数 1 在数的普通乘法中相同的作用。
令 S(M ) 表示集合 M 的全体双射变换作成的集合,于是 S(M) ⊆ T (M),即 S(M) 是 T (M ) 的
一个子集。可以证明,变换乘法也是 S(M ) 的一个代数运算,即 M 的任意两个双射变换的乘积
仍是 M 的一个双射变换。
1.4 运算律
抽象代数虽然是讨论具有代数运算的集合,但并不是讨论对代数运算不加任何限制的集合。事
实上,数、多项式、矩阵、函数等的普通运算,一般都满足通常所熟悉的运算规则,诸如结合律、
分配律或交换律等,抽象代数在研究各种代数系统时,也不能脱离开这些运算律。
定义1.20 结合律: 设 M 是一个有代数运算 ◦ 的集合,如果对 M 中任意元素 a, b, c 都有
(a ◦ b) ◦ c = a ◦ (b ◦ c)
则称 M 的这个代数运算 ◦ 满足结合律。
当然,数、多项式、矩阵及函数等对通常的加法与乘法都满足结合律。但是,一般的代数运算不
一定满足结合律。
抽象代数主要讨论满足结合律的代数运算。下面将看到,具有这种性质的代数运算会对元素的
运算带来什么影响。
设集合 M 有代数运算 ◦,现在从 M 中任取四个元素 a, b, c, d, 则写法
a ◦ b ◦ c ◦ d
应该说是毫无意义的。因为,代数运算每次只能对两个元素进行计算,四个元素只能采取加括号
的方法逐步加以计算。但易知,这四个元素共有以下五种加括号的方法:
[(a ◦ b) ◦ c] ◦ d a ◦ [(b ◦ c) ◦ d]
[a ◦ (b ◦ c)] ◦ d a ◦ [b ◦ (c ◦ d)]
(a ◦ b) ◦ (c ◦ d)
其中每一个都是 M 中一个确定的元素,当 ◦ 满足结合律时,下面将知道这五种加括号的方法的
结果是相等的,即它们是 M 中同一个元素,这是便可以不加括号,而把这个共同的元素记为
a ◦ b ◦ c ◦ d
7

1.4 运算律
在这种规定下,写法 a ◦ b ◦ c ◦ d 才有确定的意义。
一般,对 M 中 n 个元素 a
1
, a
2
, ··· , a
n
,可以证明(可以参考贾考勃逊著《抽象代数学》第一
卷)共有
s =
(2n − 2)!
n!(n − 1)!
种加括号方法,兹分别表示成
Π
1
(a
1
◦ a
2
◦ ··· ◦ a
n
) , Π
2
(a
1
◦ a
2
◦ ··· ◦ a
n
) , ··· , Π
s
(a
1
◦ a
2
◦ ··· ◦ a
n
)
定理 1.1
若集合 M 的代数运算 ◦ 满足结合律,则对 M 中任意 n ⩾ 3 个元素无论怎样加括号,其
结果都相等。
根据这个定理,对于满足结合律的代数运算来说,任意 n 个元素只要不改变元素的前后次序,就
可以任意结合而不必再加括。由于数、多项式、矩阵和线性变换的普通加法与乘法都满足结合
律,从而在对这些对象进行这两种运算时便可以任意结合,而不必加括号。这一结论不仅在中学
数学中,而且在高等代数或其他课程中从未证明过,甚至从未提及过,而现在则由上述定理全部
统一解决了。这一点充分说明,正是由于抽象代数所讨论的代数系统具有抽象性,从而决定了其
具有较广泛的应用范围。下面再讨论交换律。
定义1.21 交换律: 如果集合 M 的代数运算 ◦ 对 M 中任意元素 a, b 都有
a ◦ b = b ◦ a
则称 M 的这个代数运算 ◦ 满足交换律。
满足结合律和交换律的代数运算有以下重要意义
定理
1.2
若集合 M 的代数运算 ◦ 既满足结合律又满足交换律,则对 M 中任意 n 个元素进行运算
时可以任意结合和交换元素的前后次序,其结果均相等。
最后再讨论分配律
定义1.22 分配律: 如果集合 M 有两个代数运算 ◦ 及 ⊕,对 M 中任意元素 a, b, c 都有
a ◦ (b ⊕ c) = (a ◦ b) ⊕ (a ◦ c)
则称 ◦ 对 ⊕ 满足左分配律。如果
(b ⊕ c) ◦ a = (b ◦ a) ⊕ (c ◦ a)
则称 ◦ 对 ⊕ 满足右分配律。
定理 1.3
如果集合 M 有两个代数运算 ◦ 及 ⊕,其中 ⊕ 满足结合律,而 ◦ 对 ⊕ 满足左分配律,则
对 M 中任意元素 a 及 b
1
, b
2
, ··· , b
n
有
a ◦ (b
1
⊕ b
2
⊕ ··· ⊕ b
n
) = (a ◦ b
1
) ⊕ ··· ⊕ (a ◦ b
n
)
证明. 根据 ⊕ 满足结合律以及分配律的定义,对 n 用数学归纳法即可得证。
对右分配律有类似结论,不再赘述。
显然,结合律比分配律更为基础,因为分配律依赖于结合律。第二个定理在结合律的基础上应用
交换律,似乎又暗示了结合律比交换律更重要。经验上正是如此,结合律一般比交换律更广泛、
普遍。在介绍映射的复合时,我们可以发现其符合结合律是自明的,但其是否具有交换律则需要
8

1.4 运算律
定义。现实中,很多事物都可以抽象为映射,如果我们要求交换性,那么符合此要求的事物就会
大大减少。因此,半群,几乎是抽象代数中最基本的代数结构,它要求集合的代数运算满足结合
律,但并不要求满足交换律。
另外,正如第一个定理所述,结合律能让我们做很多事情。如果一个运算同时具有结合律和交换
律,那么毫无疑问它将是一个非常好的结构。在运算中,我们可以任意修改运算顺序和运算对
象,即可以随意对运算元素进行排列组合。如果只有结合律的话,我们只能改变运算顺序,例如
abcde = a(bc)de = abc(de)
我们可以先算 ab,也可以先算 bc 或 de,换而言之,结合律能让我们随意组合相邻元素,合成更
复杂的运算或化简运算。如果只有交换律的话,我们能做的事情就更少了
(((ab)c)d)e = (e(d(c(ba)))) = ···
无论如何都要先进行 ab 的运算,对运算的简化程度很低。
同样的,分配律也能帮助我们简化运算。如果有分配律,对于下式
a ◦
B
z }| {
(b ⊕ c ⊕ ···)
我们可以将 a 与组成 B 的任意部分进行结合。例如,我们可以利用分配律将幂运算 (5x + 2)
2
展开为 25x
2
+ 20x + 4,也可以化简含有未知量的方程
4(x − 3) = 20
4x − 12 = 20
4x − 12 + 12 = 20 + 12
4x = 32
x = 8
如果没有分配律,我们无法做到这些,甚至无法提取多项式的公因式。
9
1.4 运算律
10
第二章 线性方程组
线性方程是线性代数的起源之一,因此线性方程组可以作为代数课程首先讲述的内容。
2.1 高斯消元法
定义2.1 n 元线性方程组: 含有 n 个未知量的线性方程组称为 n 元线性方程组。
a
11
x
1
+ a
12
x
2
+ ··· + a
1n
x
n
= b
1
a
21
x
1
+ a
22
x
2
+ ··· + a
2n
x
n
= b
2
.
.
.
a
s1
x
1
+ a
s2
x
2
+ ··· + a
sn
x
n
= b
s
(2.1)
其中,每个未知量前面的数 a
11
, a
12
, ··· , a
sn
是系数,b
1
, b
2
, ··· , b
s
是常数项,常数项一般写在
等号的右边。方程的个数 s 与末知量的个数 n 可以相等,也可以是 s < n 或 s > n 的关系。
对于线性方程组 (2.1),如果 x
1
, x
2
, ··· , x
n
分别用数 c
1
, c
2
, ··· , c
n
代人后,每个方程都变成恒等式,
那么称 n 元有序数组 (c
1
, c
2
, ··· , c
n
) 是线性方程组 (2.1) 的一个解。方程组 (2.1) 的所有解组成
的集合称为这个方程组的解集。对于有实际问题背景的线性方程组,符合实际问题需要的解称
为可行解。
线性方程组的系统化解法最早出现于公元前 100 年的中国古籍《九章算术》(见《九章算术》的
第八章“方程术
1
”),随后传入日本和欧洲。虽然方程术已包含许多重要的代数运算技巧,可惜
在随后的近两千年时间中,一套较为完整的线性方程组理论并未在中国出现。今天,我们称此
算法为高斯消去法或高斯消元法 (Gaussian elimination) 以纪念德国数学家高斯 (Carl Friedrich
Gauss) 的广泛使用故而推广了这个方法。
高斯消元法的主要思想是:设法消去 n 元线性方程组的 n − 1 个未知量,剩下一个含有一个未
知量的一元一次方程,那么就能求出该未知量的值,进而得到 n −1 元线性方程组。类似地,可
以逐个求出其他未知量的值。
具体而言,在高斯消元法中,采用的主要代数运算是代入与消去 (elimination by substitution),
其目的是消去未知量,即使得未知量的系数为 0。消去运算也可以称为取代 (substitution),具体
地说,将第 j 式取代为第 i 式通乘 k 与第 j 式之和,k 6= 0,此运算依据的原理为等量公理:将
方程式等号两边同乘或同加一个非零数不会改变等式关系。取代是求解方程式的主要运算,另
外还有两个辅助运算也很管用。伸缩 (scaling) 是将某个方程式通乘一个非零数以改变方程式的
系数,原理亦为等量公理,因此方程组的解维持不变;交换 (exchange) 是置换任两个方程式的
位置,目的仅为调整方程组的阵列形式,显然此举也不会改变解。
等量公理
a, b, c 三数中,若 a = b,则:
1. a + c = b + c
2. a − c = b − c
1
今天我们所使用的“方程”一词源自于此。
11
2.1 高斯消元法
3. ac = bc
4.
a
c
=
b
c
(c 6= 0)
反之,若:
1. a + c = b + c
2. a − c = b − c
3. ac = bc (c 6= 0
4.
a
c
=
b
c
(c 6= 0)
其中一者成立,则 a = b。
定义2.2 线性方程组的初等变换: 使用高斯消元法求解线性方程组即是对线性方程组重复施行
以下三种变换。它们合称为线性方程组的初等变换。
1. 伸缩:用一非零数乘某一方程
2. 取代:把一个方程的倍数加到另一个方程
3. 交换:互换两个方程的位置
经过一系列的初等变换得到的新方程组和原方程组是同解的。显然,同解满足反身性、对称性和
传递性,因此同解是线性方程组之间的一种等价关系。
高斯消元法的具体运算,其实就是系统地用所给方程组作适当的“线性组合”,把它转换成简单
易解的形式。容易发现,高斯消元法的运算只涉及系数,与未知量无关。也就是说,在解方程组
的过程中,实际上只对各方程中各项的系数进行了运算(加、减、乘、除),每次将代表未知数
的字母抄写一遍实际上是一种累赘。为了书写的简便,更为了突出解方程组中本质的东西——系
数的运算,我们采用分离系数法(见112页),将线性方程组中代表未知数的字母略去,将等号也
略去,只写出各方程的各系数,将每个方程的各项数从左到右依次写成一行,将各方程中同一个
未知数的系数上下对齐,得到一个矩形数表,这个矩阵数表称为系数矩阵。
a
11
x
1
+ a
12
x
2
+ ··· + a
1n
x
n
= b
1
a
21
x
1
+ a
22
x
2
+ ··· + a
2n
x
n
= b
2
···
a
s1
x
1
+ a
s2
x
2
+ ··· + a
sn
x
n
= b
s
=⇒
a
11
a
12
··· a
1n
a
21
a
22
··· a
2n
.
.
.
.
.
.
.
.
.
.
.
.
a
s1
a
s2
··· a
sn
(2.2)
若将系数矩阵与等号右边的常数列并在一起,可得到此方程组的增广矩阵 (augmented matrix)。
a
11
a
12
··· a
1n
b
1
a
21
a
22
··· a
2n
b
2
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
a
s1
a
s2
··· a
sn
b
s
(2.3)
虽然,我们在这里先指出了矩阵的概念,其逻辑上也是先有了矩阵理论,
再定义方阵的行列式,但实际上,行列式
2
概念最早出现在解线性方程组
的过程中。当行列式理论发展到一定程度后,矩阵理论才发展起来,此时
才有了矩阵的数学概念。虽然如此,但作为一种简记符号,矩阵的思想很
早就萌芽。成书最迟在东汉前期的《九章算术》中,已经出现过以矩阵形
式表示线性方程组系数以解方程的图例,可算作是矩阵的雏形。
矩阵的很多性质都在行列式的研究中被讨论过(例如, 行列式行与列的变换的很多性质与矩阵的
行列变换性质基本一致),也正是行列式的研究中频繁地出现矩阵的概念,才促使数学家考虑必
须把它们作为一个实体引入数学大家庭。矩阵和行列式两个分支的共同发展, 又反过来促进了它
们自身内容的进一步深入, 矩阵理论与 19 世纪抽象代数思想的发展是不可割裂的, 它促使矩阵
作为一个重要的数学结构来研究, 从而发展出庞大的矩阵论这一数学分支。
2
十七世纪晚期,关孝和与莱布尼茨的著作中已经使用行列式来确定线性方程组解的个数以及形式。十八世纪开始,
行列式开始作为独立的数学概念被研究。十九世纪以后,行列式理论进一步得到发展和完善。
12

2.1 高斯消元法
增广矩阵完整的保留了线性方程组的所有信息,其尺寸由其所描述的方程式与未知数的数目决
定:增广矩阵的每一行 (row) 对应一个方程式的系数与常数,每一列 (column) 记录同一个未知
数的系数,最右列记录常数。表面上,矩阵以一种极为简洁的方式记录了线性方程组,隐藏的数
学意义是:矩阵让我们将线性方程组视为一个完全的独立数学物件,因此可与其他同类的物件
相比较。譬如,我们可比较两个线性方程组是否拥有相同的解。
高斯消元法的目的就是通过不改变解的运算,将繁杂的方程组型式转换为与之同解的简单型式。
由于增广矩阵的一行对应线性方程组的一个方程式,我们可以直接对增广矩阵的行执行初等变
换,此时,这称为矩阵的初等行
3
变换 (elementary row operation):
1. 将第 i 行通乘 k,k 6= 0,加到第 j 行。
2. 第 j 行通乘 k,k 6= 0。
3. 置换第 i 行和第 j 行。
类似地,可以定义矩阵的初等列变换。但我们不能对增广矩阵执行初等列变换,因为这会改变方
程组的解。显然对增广矩阵执行基本行运算
显然比起操作线性方程组方便许多,于是往后将以增广矩阵取代线性方程组。增广矩阵经过有
限次数的基本行运算转换为另一个增广矩阵,我们称这两个增广矩阵是行等价的 (row equiva-
lent)。基本行运算依循等量公理确保线性方程组的解不会改变,因此两个行等价的增广矩阵必
定有相同的解。接下来的问题是如何利用基本行运算有效地化简增广矩阵以达到求解的目的。
高斯消去法指出一条明确的求解途径:
执行一连串有效的基本行运算,直到将增广矩阵简化至与
原矩阵行等价的行阶梯形矩阵 (echelon form) ,然后使用反向代入法 (back-substitution) 可依
次解出未知数。
为了清楚描述梯形矩阵,引入以下两个定义:
定义2.3 主元 (pivot)
4
: 矩阵一行上的主元是指该行由左至右最先出现的非零元,亦称为轴元。
包含轴元的列称为轴列,包含轴元的行称为轴行。
定义2.4 零行、零列: 零行是指矩阵中所有的元皆为零的行,零列是矩阵中所有的元皆为零的列。
行阶梯形矩阵是指形如下式的矩阵,它具有两个性质:
1. 每个轴列的零元在其轴元的下方
2. 主元(首非零元)的列指标随着行指标的增加而严格增大
■ □ □ □ □
0 0 ■ □ □
0 0 0 ■ □
0 0 0 0 0
,
0 ■ □ □ □ □ □
0 0 ■ □ □ □ □
0 0 0 0 ■ □ □
0 0 0 0 0 ■ □
其中轴元 (以 ■ 表示) 是任意非零数,轴行中排在轴元之后的元 (以 □ 表示) 可以是任意数。
高斯消去法实际作法利用主元以消去其下方的所有元,这解释了为何主元不得为零。
以上消去过程显示仅须行使取代与交换运算便可将给定的矩阵转化成梯形,但因为消去程序可
能有多种行交换方式,最后产生的梯形矩阵也因此不同。值得注意的是,不论如何进行消去程
序,梯形矩阵的轴元位置总是固定的,这个现象可由观察确认 (严格的证明请见“简约列梯形式
的唯一性”)。
高斯消去法得到梯形增广矩阵后,我们的求解工作已近尾声,接下来可以用反向代入法限制并解
出各个未知数。但我们还可以让梯形矩阵变得更简单些,也就是得到简化行阶梯矩阵,此时可以
直接写出方程组的解(若有解)。简化行阶梯矩阵是形如下式的矩阵,它具有四个性质:
1. 本身是阶梯形矩阵
3
大陆的“行”相当于台湾的“列”,因为台湾书籍惯用竖向排版。
4
台湾教材称之为轴元或领先元,英文称为 pivot,含义为 diagonal entries of determinant.
13

2.1 高斯消元法
2. 主元全为 1
3. 主元所在列其余元素全为 0
■ □ 0 0 □
0 0 ■ 0 □
0 0 0 ■ □
0 0 0 0 0
,
0 ■ 0 □ 0 0 □
0 0 ■ □ 0 0 □
0 0 0 0 ■ 0 □
0 0 0 0 0 ■ □
其中主元 (以 ■ 表示) 为 1,以 □ 表示的元可以是任意数。
下面来证明高斯消元法确实是有效的,即高斯消元法能应用于任意多个方程、未知量的线性方程
组。这等价于证明以下定理。
定理
2.1
任意一个矩阵都可以经过一系列初等行变换化成阶梯形矩阵。
证明. 零矩阵按定义是阶梯形矩阵。下面考虑非零矩阵,对非零矩阵的行数 s 使用数学归纳法。
s = 1 时,矩阵只有一行,这是阶梯形矩阵。
假设 s −1 行的矩阵都能经过初等行变换化成阶梯形矩阵。下面看 s 行的矩阵 A,它的 (i, j) 元
用 a
ij
表示。
如果 A 的第 1 列元素不全为 0,那么互换两行位置可以使矩阵的 (1, 1) 元不为 0 ,因此 不妨设
A 的 (1, 1) 元 a
11
6= 0,把 A 的第 1 行的 −
a
21
a
11
倍加到第 2 行,第 1 行的 −
a
31
a
11
倍加到第 3 行,
···,第 1 行的 −
a
s1
a
11
倍加到第 s 行,A 变成下述矩阵 B:
B =
a
11
a
12
··· a
1n
0 a
22
−
a
21
a
11
a
12
··· a
2n
−
a
21
a
11
a
1n
.
.
.
.
.
.
.
.
.
0 a
s2
−
a
s1
a
11
a
12
··· a
sn
−
a
s1
a
11
a
1n
把 B 的右下方的 (s −1) ×(n −1) 矩阵记作 B
1
。如果 A 的第 1 列元素全为 0,那么考虑 A 的
第 2 列。若 A 的第 2 列元素不全为 0,不妨设 a
12
6= 0,把 A 的第 1 行的适当倍数分别加到第
2, 3, ··· , s 行上,可以把 A 变成下 述矩阵 C:
C =
0 a
12
a
13
··· a
1n
0 0 a
23
−
a
22
a
12
a
13
··· a
2n
−
a
22
a
12
a
1n
.
.
.
.
.
.
.
.
.
.
.
.
0 0 a
s3
−
a
s2
a
12
a
13
··· a
sn
−
a
s2
a
12
a
1n
,
把矩阵 C 的右下方的 (s −1) × (n −2) 矩阵记作 C
1
。如果 A 的第 1、2 列元素全都为 0,那么
考虑 A 的第 3 列,以此类推。
由于 B
1
, C
1
, ··· 都是 s − 1 行矩阵,根据归纳假设,它们可以经过初等行变换分别化成阶梯形
矩阵 J
1
, J
2
, ···。因此,A 可以经过初等行变换化成下述形式的矩阵之一:
a
11
a
12
··· a
1n
0
.
.
. J
1
0
,
0 a
12
a
13
··· a
1n
0 0
.
.
.
.
.
. J
2
0 0
, ···
这些都是阶梯形矩阵。根据数学归纳法原理,对于任意正整数 s,s 行非零矩阵都可以经过初等
行变换化成阶梯形矩阵。
推断 2.1-1 任意一个矩阵都可以经过一系列初等行变换化成简化行阶梯形矩阵。
14
2.2 解的情况及其判别准则
2.2 解的情况及其判别准则
使用高斯消元法最终得到阶梯形线性方程组:
c
11
x
1
+ c
12
x
2
+ ··· + c
1r
x
r
+ ··· + c
1n
x
n
= d
1
c
22
x
2
+ ··· + c
2r
x
r
+ ··· + c
2n
x
n
= d
2
···
c
rr
x
r
+ ··· + c
rn
x
n
= d
r
0 = d
r+1
0 = 0
···
0 = 0
(2.4)
其中 c
ii
6= 0, i = 1, 2, ··· , r。如果方程组中出现 0 = 0 的恒等式,去掉即可。
分析一下解的情况:n 元线性方程组解的情况有且只有 3 种情况,即无解、唯一解、无穷多个解。
1. 如果 d
r+1
6= 0,与 0 = d
r+1
矛盾,显然无解。
2. 当 d
r+1
是零或着没有 0 = 0 的方程时,分两种情况(n 是变量的个数,r 是方程个数):
(a) r = n,唯一解
(b) r < n,无穷多个解。
此时,方程组的解集的特点是:等号左边是主变量,右边是常数和自由未知量。
主变量:以主元为系数的未知量
自由未知量:主变量以外的未知量。
(c) r > n,不可能出现这种情况。
当方程的数量比未知量数量多的时候,多出来的方程一定会消去,变成 0 = 0 恒等式。
2.4式是线性方程组的一般形式,如果等号右边全为 0,则称为齐次线性方程组,它是一种特殊情
况,自然也符合上述解的情况。
a
11
x
1
+ a
12
x
2
+ ··· + a
1n
x
n
= 0
a
21
x
1
+ a
22
x
2
+ ··· + a
2n
x
n
= 0
······
a
s1
x
1
+ a
s2
x
2
+ ··· + a
sn
x
n
= 0
(2.5)
对于任何齐次线性方程组,零解就已经是一个解。所以,齐次线性方程组不会出现无解的情形,
而当 r = n,齐次线性方程组只有零解。因此,有如下定理:
定理 2.2. 齐次线性方程组非零解存在定理
在齐次线性方程组中(如2.5式),如果 s < n,那么它必有非零解。
证明. 2.5式中,s 代表方程的个数;由前面的叙述可知,若阶梯形线性方程组的方程个数 r 少
数未知量的个数 n,则2.5式有非零解。因为 r ≤ s,若 s < n,则必有 r < n,亦即2.5式有非零
解。
现在讨论线性方程组的解的情况是基于阶梯形矩阵(方程组)的,有没有方法在不进行初等变换
的情况下就能判断解的情况呢?
2.3 快速消元法与行列式的递归定义
上一节介绍了高斯消元法求解线性方程组,你可以发现高斯消元法虽简单,但十分繁琐。如果是
一个含有三个方程的三元线性方程组,消去第一个未知量要两次初等变换,消去第二个未知量
15

2.3 快速消元法与行列式的递归定义
要一次初等变换,一共需要三步才求解出其中一个未知量的值。而求出三个未知量的值则需要
3 × 3 = 9 步。这仅仅是三个未知量的情况,如果未知量个数更多,则需要更多次初等变换。
这显然是很低效的,有没有高效一些的运算方法在不进行初等变换的情况下就能判断解的情况,
甚至求出唯一解呢?如果有一步到位的方法自然最好。抱着这样的目的,数学家着手研究,研究
成果即是行列式。
一般来说,中国大陆(不包括香港)21 世纪以来的教材一般直接给出“n 阶行列式的展开式”来
作定义,但是这样便需要对排列群 (permutation group)(或称作对称群,symmetricgroup)有
一定的认识才可以妥善地做好。因为五阶行列式展开后共有 120 项,六阶行列式展开后共有 720
项,而一般地 n 阶行列式展开后共有 n! 项,所以对于初学者或是对排列群认识不深的人来说,
直接使用展开式来作讨论是难以胜任自如的。想当年 Cramer 和 Vandermonde 乃是非常优秀的
代数学家,而且他们对于排列群又有着深刻的认识,所以他们才直截了当地处理那个巨大的展开
公式;但对于一般人来说,这样讨论行列式肯定是吃力难懂的。
在基础数学中,从逻辑来看,行列式有两个自然的源起:其一是 n 阶线性方程组的基础理论,其
二则是 n 维平行体的高维有向体积 (high dimensional oriented volume)。但从历史来看,
行列式最早源于对 n 阶线性方程组唯一解条件的探索,人们由此发现了一种快速的高斯消元法,
并将之定义为行列式。到了后来,人们又发现了有向体积也是行列式。
很多教材是先讲行列式,给出其展开式作为定义,后讲线性方程组。这会让不少读者困惑于行列
式为何而来,又为何恰好可以作为解线性方程组的工具。
2.3.1 二阶和三阶行列式
那么高斯消元法是如何定义行列式的呢?回到线性方程组的基本问题:
在什么条件之下,一组 n 个 n 元线性方程具有唯一解?再者,在满足唯一解条件的
情形,试求以方程组系数表达其唯一解组之公式。
当 n = 1 时,解答很简单,但它提供了我们一个起点,所以我们先把这时的结果写出如下。
ax = b
当 a 6= 0 时有唯一解,其解公式为 x =
b
a
。
接着讨论 n = 2 的情形。设方程组为
(
a
1
x + b
1
y = c
1
1
a
2
x + b
2
y = c
2
2
为求出 x 的解,要先消去 y,下述方法可以做到:b
2
× 1 − b
1
× 2 ,整理可得
(a
1
b
2
− a
2
b
1
)x = c
1
b
2
− c
2
b
1
所以,如果 (a
1
b
2
−a
2
b
1
) 6= 0,则 x 的解是唯一的。若 (a
1
b
2
−a
2
b
1
) = 0,则方程可能无解或有
无穷解。至于 y 的解,同理,a
2
× 1 − a
1
× 2 可得到
(a
2
b
1
− a
1
b
2
)y = c
1
a
2
− c
2
a
1
由此可见,同样的条件 (a
1
b
2
− a
2
b
1
) 6= 0 也可以保证 y 的解是唯一的,亦即方程有唯一解的充
要条件是 (a
1
b
2
− a
2
b
1
) 6= 0。当这个条件成立时,x 和 y 的解可以分别用下述公式表示:
x =
c
1
b
2
− c
2
b
1
a
1
b
2
− a
2
b
1
y =
a
1
c
2
− a
2
c
1
a
1
b
2
− a
2
b
1
这个就是我们想探求者在 n = 2 时的情形。我们发现方程组的解的唯一性是取决于某一个量是
16

2.3 快速消元法与行列式的递归定义
否不为 0
5
,亦即
(
a
1
x + b
1
y = c
1
a
2
x + b
2
y = c
2
当(a
1
b
2
− a
2
b
1
) 6= 0有唯一解。 (2.6)
上述结果和 n = 1 的情形很类似,实际上这点并非偶然,这就是我们企图用归纳法证明的问题。
在此引进二阶行列式的记号,并用2.6式唯一解的条件来定义:
a
1
b
1
a
2
b
2
= a
1
b
2
− a
2
b
1
上述代数表达式称为该方程组系数的「二阶行列式」,相当于 (a
1
b
2
−a
2
b
1
) 的另一种写法(我们
也定义对应于 ax = b 的「一阶行列式」为 a 本身)。当这个二阶行列式不为 0 时,x, y 就会有
唯一解,而且其唯一解之公式就可以用上述符号如下表达之,亦即:
x =
c
1
b
2
− c
2
b
1
a
1
b
2
− a
2
b
1
=
c
1
b
1
c
2
b
2
a
1
b
1
a
2
b
2
y =
a
1
c
2
− a
2
c
1
a
1
b
2
− a
2
b
1
=
a
1
c
1
a
2
c
2
a
1
b
1
a
2
b
2
当 n = 3 时,设方程组为:
a
1
x + b
1
y + c
1
z = d
1
1
a
2
x + b
2
y + c
2
z = d
2
2
a
3
x + b
3
y + c
3
z = d
3
3
因为 c
1
, c
2
, c
3
至少有一个不为零,不失一般性,设 c
2
6= 0,则通过 c
2
×
1
− c
1
×
2
先消去 z:
(a
1
c
2
− a
2
c
1
) x + (b
1
c
2
− b
2
c
1
) y = d
1
c
2
− d
2
c
1
4
通过 c
3
× 2 − c
2
× 3 :
(a
2
c
3
− a
3
c
2
) x + (b
2
c
3
− b
3
c
2
) y = d
2
c
3
− d
3
c
2
5
再通过 (b
2
c
3
− b
3
c
2
) × 4 − (b
1
c
2
− b
2
c
1
) × 5 消去 y:
{(a
1
c
2
− a
2
c
1
) (b
2
c
3
− b
3
c
2
) − (a
2
c
3
− a
3
c
2
) (b
1
c
2
− b
2
c
1
)}x
= {(d
1
c
2
− d
2
c
1
) (b
2
c
3
− b
3
c
2
) − (d
2
c
3
− d
3
c
2
) (b
1
c
2
− b
2
c
1
)}
6
通过以上三个步骤,方程组变为如下:
■x + 0y + 0z = ■
■x + ■y + 0z = ■
a
3
x + b
3
y + c
3
z = d
3
其中 ■ 代表某个数。当我们消去 y, z 之后,展开
6
式中 x 的系数时,发现所得的 8 项之中只
有 2 项是不含有 c
2
者,而且它们刚好互相抵消。同样情况亦出现在右方的常数项,所以我们可
以提出公因子 c
2
,并且将 6 重写成:
c
2
(a
1
b
2
c
3
− a
1
b
3
c
2
+ a
2
b
3
c
1
− a
2
b
1
c
3
+ a
3
b
1
c
2
− a
3
b
2
c
1
) x
= c
2
(d
1
b
2
c
3
− d
1
b
3
c
2
+ d
2
b
3
c
1
− d
2
b
1
c
3
+ d
3
b
1
c
2
− d
3
b
2
c
1
)
为何 c
2
会成为公因子呢?原因是当初我们用了两次 2 式来消去 z,而其中 c
2
是乘了两次的。
由此得出 x 有唯一解的充要条件为
5
这句话的意思是:只剩下一个变元时,无论是哪个变元,它们的系数的绝对值是一样的。
17

2.3 快速消元法与行列式的递归定义
a
1
b
2
c
3
− a
1
b
3
c
2
+ a
2
b
3
c
1
− a
2
b
1
c
3
+ a
3
b
1
c
2
− a
3
b
2
c
1
6= 0 (2.7)
上式可重写为
a
1
(b
2
c
3
− b
3
c
2
) − a
2
(b
1
c
3
− b
3
c
1
) + a
3
(b
1
c
2
− b
2
c
1
) 6= 0 (2.8)
仔细观察,上式那些 (b
2
c
3
− b
3
c
2
) 其实是 y, z 某部分系数的二阶行列式。例如 (b
2
c
3
− b
3
c
2
) 是
把 a
1
所在的行( 1 式)和列 (x 的系数) 删掉而计算余下系数的行列式。由此「后见之明」可
以看到了一 个更好的做法, 即我们只需直接考虑:
(b
2
c
3
− b
3
c
2
) × 1 − (b
1
c
3
− b
3
c
1
) × 2 + (b
1
c
2
− b
2
c
1
) × 3
则 y, z 就可以 一蹴而成 地全被消去,并且可以直接得出 (在此不需假设 c
2
6= 0)
a
1
b
2
c
2
b
3
c
3
− a
2
b
1
c
1
b
3
c
3
+ a
3
b
1
c
1
b
2
c
2
x = d
1
b
2
c
2
b
3
c
3
− d
2
b
1
c
1
b
3
c
3
+ d
3
b
1
c
1
b
2
c
2
(2.9)
上述有效的消元法让我们坚信2.8式是比2.7式更能突出其要点, 用2.8式来定义三阶行列式要比
用2.7式来得顺当自然, 即:
a
1
b
1
c
1
a
2
b
2
c
2
a
3
b
3
c
3
= a
1
b
2
c
2
b
3
c
3
− a
2
b
1
c
1
b
3
c
3
+ a
3
b
1
c
1
b
2
c
2
用上述三阶行列式的符号,重写2.9式,可得
a
1
b
1
c
1
a
2
b
2
c
2
a
3
b
3
c
3
x =
d
1
b
1
c
1
d
2
b
2
c
2
d
3
b
3
c
3
(2.10)
而相对于 y 和 x 时的情形,我们同样可得
a
1
b
1
c
1
a
2
b
2
c
2
a
3
b
3
c
3
y =
a
1
d
1
c
1
a
2
d
2
c
2
a
3
d
3
c
3
a
1
b
1
c
1
a
2
b
2
c
2
a
3
b
3
c
3
z =
a
1
b
1
d
1
a
2
b
2
d
2
a
3
b
3
d
3
(2.11)
上述三个公式便是著名的 Cramer rules 在三个三元一次方程的情形。总结上述三元的讨论,即
有
a
1
x + b
1
y + c
1
z = d
1
a
2
x + b
2
y + c
2
z = d
2
a
3
x + b
3
y + c
3
z = d
3
当
a
1
b
1
c
1
a
2
b
2
c
2
a
3
b
3
c
3
6= 0 时有唯一解
并且这个唯一解可以用2.10式和2.11式表达之。再者,若2.10式和2.11式左边的系数为 0,且右边
不为 0 时,显然方程组无解。若作右边也为 0,则三个方程其中之一可用另外两个方程表示。
2.3.2 四阶行列式
对于四个四元线性方程:
a
1
x + b
1
y + c
1
z + d
1
w = e
1
1
a
2
x + b
2
y + c
2
z + d
2
w = e
2
2
a
3
x + b
3
y + c
3
z + d
3
w = e
3
3
a
4
x + b
4
y + c
4
z + d
4
w = e
4
4
我们当然可以运用消元法先消去 w,再消去 z,最后消去 y,得到只剩 x 的等式。但是在 n = 3
的情形,我们已经发现了一个更为有效的方法可以一蹴而成地消去其他变元,所以依样画葫芦地
18

2.3 快速消元法与行列式的递归定义
来试一试其法是否依然可行,即
b
2
c
2
d
2
b
3
c
3
d
3
b
4
c
4
d
4
×
1
−
b
1
c
1
d
1
b
3
c
3
d
3
b
4
c
4
d
4
×
2
+
b
1
c
1
d
1
b
2
c
2
d
2
b
4
c
4
d
4
×
3
−
b
1
c
1
d
1
b
2
c
2
d
2
b
3
c
3
d
3
×
4
如上述方法是可行的,则 x 的系数便是我们所求的「四阶行列式」,亦即
a
1
b
1
c
1
d
1
a
2
b
2
c
2
d
2
a
3
b
3
c
3
d
3
a
4
b
4
c
4
d
4
= a
1
b
2
c
2
d
2
b
3
c
3
d
3
b
4
c
4
d
4
− a
1
b
1
c
1
d
1
b
3
c
3
d
3
b
4
c
4
d
4
+ a
3
b
1
c
1
d
1
b
2
c
2
d
2
b
4
c
4
d
4
− a
4
b
1
c
1
d
1
b
2
c
2
d
2
b
3
c
3
d
3
(2.12)
上述依样试用的消元法所得的 y, z, w 的系数分别如下,所以此法是否依然可以一蹴而成地消去
y, z, w,当然就取决于的 y, z, w 的系数是否都自然而然地为 0!亦即
b
1
b
2
c
2
d
2
b
3
c
3
d
3
b
4
c
4
d
4
− b
2
b
1
c
1
d
1
b
3
c
3
d
3
b
4
c
4
d
4
+ b
3
b
1
c
1
d
1
b
2
c
2
d
2
b
4
c
4
d
4
− b
4
b
1
c
1
d
1
b
2
c
2
d
2
b
3
c
3
d
3
?
= 0
c
1
b
2
c
2
d
2
b
3
c
3
d
3
b
4
c
4
d
4
− c
2
b
1
c
1
d
1
b
3
c
3
d
3
b
4
c
4
d
4
+ c
3
b
1
c
1
d
1
b
2
c
2
d
2
b
4
c
4
d
4
− c
4
b
1
c
1
d
1
b
2
c
2
d
2
b
3
c
3
d
3
?
= 0
d
1
b
2
c
2
d
2
b
3
c
3
d
3
b
4
c
4
d
4
− d
2
b
1
c
1
d
1
b
3
c
3
d
3
b
4
c
4
d
4
+ d
3
b
1
c
1
d
1
b
2
c
2
d
2
b
4
c
4
d
4
− d
4
b
1
c
1
d
1
b
2
c
2
d
2
b
3
c
3
d
3
?
= 0
(2.13)
用四阶行列式的定义(2.12式),它们可以分别改写如下
b
1
b
1
c
1
d
1
b
2
b
2
c
2
d
2
b
3
b
3
c
3
d
3
b
4
b
4
c
4
d
4
c
1
b
1
c
1
d
1
c
2
b
2
c
2
d
2
c
3
b
3
c
3
d
3
c
4
b
4
c
4
d
4
d
1
b
1
c
1
d
1
d
2
b
2
c
2
d
2
d
3
b
3
c
3
d
3
d
4
b
4
c
4
d
4
(2.14)
我们可以展开以上四个行列式,就可以验证它们的确恒等于零,但可预见随着行列式的阶数增
加,这种做法就越来越繁琐。因此,我们需要寻求的出路是对行列式的性质作深入探讨。像2.13式
这样的公式能普遍成立,我们相信此时绝非偶然,肯定有其本质的原因。
我们可以看到2.14式的行列式比较特别,它们全是有两列 (columns) 完全一样的四阶行列式。所
以,若我们能够证明任何有两列全同的行列式的值恒为 0(这种特性称之为交错性 (alternating
property)),则2.13式(快速消元法)就会普遍成立。可惜这个方法涉及寻找四阶行列式的确实
数值,所以仍受着繁复公式的牵制,我们不妨避重就轻,改为研讨下述的「特性」。
「把一个行列式中的两列互换时,它的新旧值是否只相差一个负号?」
若上述特性(称之为「斜对称性」(skew-symmetric property))能够普遍成立,则只需把两个全
同之列互换,例如:
b
1
b
1
c
1
d
1
b
2
b
2
c
2
d
2
b
3
b
3
c
3
d
3
b
4
b
4
c
4
d
4
= −
b
1
b
1
c
1
d
1
b
2
b
2
c
2
d
2
b
3
b
3
c
3
d
3
b
4
b
4
c
4
d
4
即说明此类行列式的值必为 0。于是这种「行列式的快速消元」是可行的。
交错性与斜对称性在一般抽象环、域的行列式理论中是有少许差别的,但在这里我们可以
把它们当作同一样的概念。
19

2.3 快速消元法与行列式的递归定义
2.3.3 归纳证明
接下来要做的就是通过归纳法证明出斜对称性普遍成立,由此可得出 n 阶行列式的归纳定义,并
且 n 个 n 元方程的唯一解条件使用行列式表示,即是 Cramer 法则。
1 对于二阶行列式,由其定义式可知
a
1
b
1
a
2
b
2
= a
1
b
2
− a
2
b
1
= −(b
1
a
2
− b
2
a
1
) = −
b
1
a
1
b
2
a
2
所以斜对称性在 n = 2 时成立。
2 对于三阶行列式,有三种互换方法要考虑,如互换第一列和第二列:
a
1
b
1
c
1
a
2
b
2
c
2
a
3
b
3
c
3
= a
1
b
2
c
3
− a
1
b
3
c
2
+ a
2
b
1
c
3
+ a
3
b
1
c
2
− a
3
b
2
c
1
= −(b
1
a
2
c
3
− b
1
a
3
c
2
+ b
2
a
3
c
1
− b
2
a
1
c
3
+ b
3
a
1
c2 − b
3
a
2
c
1
)
= −
b
1
a
1
c
1
b
2
a
2
c
2
b
3
a
3
c
3
同理可证馀下的两种互换方法,即互换第一列和第三列,及互换第二列和第三列。斜对称性在
n = 3 时亦成立
3 对于四阶行列式,上述的直接验证方法很费时。在此,我们将改用性质来证明。首先回顾四
阶行列式的定义式(2.12式):
D =
a
1
b
1
c
1
d
1
a
2
b
2
c
2
d
2
a
3
b
3
c
3
d
3
a
4
b
4
c
4
d
4
= a
1
D
1,1
− a
2
D
2,1
+ a
3
D
3,1
− a
4
D
4,1
(2.15)
在这里我们引入了简约符号 D
i,j
,它代表把原来的四阶行列式内的第 i 行和第 j 列删去后,所
得的三阶行列式。例如
D
2,1
=
a
1
b
1
c
1
d
1
a
2
b
2
c
2
d
2
a
3
b
3
c
3
d
3
a
4
b
4
c
4
d
4
=
b
1
c
1
d
1
b
3
c
3
d
3
b
4
c
4
d
4
由上述重写的定义式2.15的可以看到,若在原来的四阶行列式中所互换的两列不涉及第 1 列,则
以上每一个 D
i,1
都有相应的换列发生:由已知的 n = 3 的情形得知每个 D
i,1
也转作 −D
i,1
,因
此原来的四阶行列式 D 也转为 −D。余下只需验证涉及第 1 列的换列。
稍加分析后,我们只需集中讨论第 1 列和第 2 列的互换。例如,第 1 列和第 3 列的互换可用下
述一串换列来得出。
0. 起始: A—B—C—D
1. 互换第 2 列和第 3 列: A—C—B—D
2. 互换第 1 列和第 2 列: C—A—B—D
3. 互换第 2 列和第 3 列: C—B—A—D
由于第 1 步和第 3 步都引入一个负号,所以其作用互相抵消,若可验证第 2 步也同样地引入一
个负号,则换列涉及第 1 列的验证便可完成。
在行列式的定义式2.15中,第一列是有别于其余各列的,因为用来写下定义式的系数是取于第一
20

2.3 快速消元法与行列式的递归定义
列者,而其他列的系数则全都统括在那些低一阶的子行列式内。所以,当第一列和第二列互换
后,看起来定义式便会变得面目全非、难以处理。因此,我们先要做一些准备功夫,把那些三阶
行列式再进一步分解下去,即将原来四阶行列式的第 2 列系也提出来,这样第 2 列和第 1 列系
数便可以处于同等地位。例如:
D
1,1
=
b
2
c
2
d
2
b
3
c
3
d
2
b
4
c
4
d
4
= b
2
c
3
d
3
c
4
d
4
− b
3
c
2
d
2
c
4
d
4
+ b
4
c
2
d
2
c
3
d
3
= b
2
D
12,12
− b
3
D
13,12
+ b
4
D
14,12
当我们把2.15式中的四个三阶子行列式如前述分解后,便得出:
D =a
1
(b
2
D
12,12
− b
3
D
13,12
+ b
4
D
14,12
)
−a
2
(b
1
D
12,12
− b
3
D
23,12
+ b
4
D
24,12
)
+a
3
(b
1
D
13,12
− b
2
D
23,12
+ b
4
D
34,12
)
−a
4
(b
1
D
14,12
− b
2
D
24,12
+ b
3
D
34,12
)
=(a
1
b
2
− a
2
b
1
)D
12,12
+ (a
3
b
1
− a
1
b
3
)D
13,12
+ (a
1
b
4
− a
4
b
1
)D
14,12
+ (a
2
b
3
− a
3
b
2
)D
23,12
+ (a
4
b
2
− a
2
b
4
)D
24,12
+ (a
3
b
4
− a
4
b
3
)D
34,12
由上式我们立即可看到若把的第 1 列和第 2 列互换(即把 a
i
和 b
i
互 换),则每个 D
ij,12
保持
不变,但其系数却都引进了负号,所以整体上 D 便转为 −D。斜对称性得,所以「有效消元法」
在 n = 4 时依然可行。
4 现在让我们先正式地定义 n 阶行列式。考虑下述 n 个 n 元一次的线性方程组(n > 3)
a
11
x
1
+ a
12
x
2
+ ··· + a
1n
x
n
= b
1
a
21
x
1
+ a
22
x
2
+ ··· + a
2n
x
n
= b
2
···
a
n1
x
1
+ a
n2
x
2
+ ··· + a
nn
x
n
= b
n
(2.16)
则由它的系数集所得的 n 阶行列式 D 定义为
D =
a
11
a
12
···
a
1n
a
21
a
22
··· a
2n
.
.
.
.
.
.
.
.
.
.
.
.
a
n1
a
n2
··· a
nn
= a
11
D
1,1
− a
21
D
2,1
+ ··· + (−1)
n+1
a
n1
D
n,1
=
n
P
i=1
(−1)
i+1
a
i1
D
i,1
(2.17)
其中每一个 D
i,1
, 1 ≤ i ≤ n,都是低一阶的子行列式,它们把原来 n 阶行列式内的第 i 行和第
1 列删去。
现在让我们来归纳地证明2.17式定义的 n 阶行列式就是我们所需求者,要点在于验证其斜对称
性。归纳假设所有不高于 n − 1 阶的行列式(n ≥ 3)已具有斜对称性,我们把 n 阶行列式的换
列分成下述两种情形来考虑:
一、不涉及第 1 列的换列
从定义式2.17可以直接看到,其中每一个 D
i,1
也都有相应的换列,由归纳假设知道这种换列使
得每一个 D
i,1
变为 −D
i,1
,而 a
i,1
则全部不变,易见这种换列使得 D 变为 −D。
二、第 1 列和第 k 列的互换
这个情况和在讨论四阶行列式的斜对称性证明时一样,我们只需集中讨论第 1 列和第 2 列的互
换。而验证的方法则是把那些 D
i,1
分别再用 (n − 1) 阶行列式的归纳定义式展开成一些 (n − 2)
阶子行列式(即 D
ij,12
)的倍数和,然后研讨最后所得的展开式中每一个的系数在上述换列后的
21

2.4 CRAMER 法则
变化。D
ij,12
的定义是把 D 的第 i 行和第 j 行、以及第 1 列和第 2 列删去,所得的 (n − 2) 阶
子行列式。易见可以有下述两种途径得出含有 D
ij,12
者:
(i) 从 D
i,1
中删掉相对于 D 的第 j 行和第 2 列
(ii) 从 D
j,1
中删掉相对于 D 的第 i 行和第 2 列
可参考下述图示:
图 2.1: 得到 D
ij,12
的途径
不失一般性,这里假设 i < j 。在方法 (i) 中得到的 D
ij,12
,其系数(在 D 中展开)为
(−1)
i+1
a
i1
· (−1)
(j−1)+1
a
j2
= (−1)
i+j+1
a
i1
a
j2
在方法 (ii) 中而得到的 D
ij,
12
,其系数为
(−1)
j+1
a
j1
· (−1)
i+1
a
i2
= (−1)
i+j+2
a
j1
a
i2
于是在 D 的展开中,D
ij,12
是以下述形式出现的:
D = ··· + (−1)
i+j+1
(a
i1
a
j2
− a
j1
a
i2
)D
ij,12
+ ···
由此可见,当 D 的第 1 列和第 2 列互换后,即 a
i1
↔ a
i2
, a
j1
↔ a
j2
,那么展开式中 D
ij,12
的系
数变为:
a
i1
a
j2
− a
j1
a
i2
→ a
i2
a
j1
− a
j2
a
i1
= −(a
i1
a
j2
− a
j1
a
i2
)
总括来说,当 D 的第 1 列和第 2 列互换后,在它的上述表成 (n − 2) 阶子行列式中 D
ij,12
的展
开中,每个中 D
ij,12
保持不变,但其系数则变号,所以整体上对中 D 的影响是中 D → −D。斜
对称性得证。
2.4 Cramer 法则
从上面的叙述可知,对于如下线性方程组:
a
11
x
1
+ a
12
x
2
+ ··· + a
1
n
x
n
= b
1
a
21
x
1
+ a
22
x
2
+ ··· + a
2n
x
n
= b
2
···
a
n1
x
1
+ a
n2
x
2
+ ··· + a
nn
x
n
= b
n
(2.18)
利用行列式的斜对称性,可以解出 x
1
:
a
11
a
12
··· a
1n
a
21
a
22
··· a
2n
.
.
.
.
.
.
.
.
.
.
.
.
a
n1
a
n2
··· a
nn
x
1
=
b
1
a
12
··· a
1n
b
2
a
22
··· a
2n
.
.
.
.
.
.
.
.
.
.
.
.
b
n
a
n2
···
a
nn
可以解出 x
2
,并变形为类似 x
1
的解的形式,其余变量的解同理:
22

2.5 后话——LAPLACE 公式与平行多面体有向体积
a
12
a
11
··· a
1
n
a
22
a
21
··· a
2n
.
.
.
.
.
.
.
.
.
.
.
.
a
n2
a
n1
··· a
nn
x
2
=
b
1
a
11
··· a
1
n
b
2
a
21
··· a
2n
.
.
.
.
.
.
.
.
.
.
.
.
b
n
a
n1
··· a
nn
⇓
a
11
a
12
··· a
1n
a
21
a
22
··· a
2n
.
.
.
.
.
.
.
.
.
.
.
.
a
n1
a
n2
··· a
nn
x
2
=
a
11
b
1
··· a
1n
a
12
b
2
··· a
2n
.
.
.
.
.
.
.
.
.
.
.
.
a
1n
b
n
··· a
nn
定理 2.3. Cramer 法则
如果2.18式的线性方程组的系数矩阵的行列式 D = |A| 6= 0,则方程组有唯一解,并且解
为:
x
1
=
D
1
D
, x
2
=
D
2
D
, ··· , x
n
=
D
n
D
其中 D
j
(j = 1, 2, ··· , n) 是把行列式 D 中第 j 列的元素用方程组的常数项 b
1
, b
2
, ··· , b
n
代换所得的一个 n 阶行列式,即
D
j
=
a
11
··· a
1,j−1
b
1
a
1,j+1
··· a
1n
a
21
··· a
2,j−1
b
2
a
2,j+1
··· a
2n
··· ··· ··· ··· ··· ··· ···
a
n1
··· a
n,j−1
b
n
a
n,j+1
··· a
nn
注意,克莱姆法则只能用于方程的个数与未知量个数相等且系数行列式不等于零的线性方程组。
如果方程个数多于未知量个数,可以通过消元法消去多余的方程,使得两者相等。若2.18式的系
数矩阵行列式 D 为 0,且存在一个未知量 x
i
对应的 D
i
不为零,显然无解;若 D 为零,且所
有 D
i
也为零,则有无穷解。
在实际运算中,当矩阵的维数较高时,计算行列式是非常困难的。也就是说,计算行列式的时间
复杂度随维数的增长非常快,对于一个 n 阶的方阵,使用行列式定义的公式计算,其时间复杂
度是 O( n!)。克莱姆法则虽然直接给出了线性方程组的解,但由于其适用条件的限制和直接根据
系数矩阵计算其行列式非常困难,因此,在实际计算中并未被采用。
推断 2.3-1 若是齐次线性方程组,那么 D = |A| 6= 0,此时只有零解。如果齐次线性方程组有非
零解,那么一定有 |A| = 0。
推断 2.3-2 如果非齐次线性方程组无解或有两个不同的解,则它的系数行列式必为零。
如何记住 Cramer 法则(解的情况)呢?
Cramer 法则是解线性方程组的一般方法,我们找一个特殊的方程(组)来协助记忆即可:
Ax = b
当 A 6= 0 时,有唯一解;当 A = 0 且 b 6= 0,无解; 当 A = 0 且 b = 0,无穷解。
2.5 后话——Laplace 公式与平行多面体有向体积
对于求解线性方程组来说,行列式本质上就是一种快速消元法,其递归公式由归纳法推导出。行
列式的递归定义又被称为「行列式按列(行)展开」,后来,行列式的递归公式又被推广出拉普
拉斯公式
数学家在后来的研究中发现,同样符合斜对称性和多线性的有向体积(莱布尼兹公式)和行列式
是同一个东西。由此,行列式与几何产生联系,有了几何意义。再后来,人们为了确定行列式每
一项的正负号,引入了排列的概念,从而行列式又可以借助排列来定义。
23
2.5 后话——LAPLACE 公式与平行多面体有向体积
行列式的归纳式定义最自然、顺理成章的,但是一般教材都直接采用 n 阶行列式展开式(排列
式)来定义行列式。这是违背数学直觉的做法,但为什么教材喜欢这么编写呢?猜测其中一个原
因是:用递归法(降阶法)定义行列式时,完整地证明行列式的基本性质是困难的,有些教材为
此花费了较多篇幅(如蓝以中的《线性代数引论》),更多的是对行列式的两个基本性质(转置、
换行)避而不证。
24
第三章 行列式
3.1 斜对称多线性函数与行列式的界定定理
为了方便讨论 n 阶行列式的其他性质,在此引入列向量的记号。令
a
i
=
a
1i
a
2i
.
.
.
a
ni
b =
b
1
b
2
.
.
.
b
n
e
i
=
0
.
.
.
1
i处
.
.
.
0
其中,e
i
是标准基底向量。
列向量的加和乘积运算是直接用其分量加以定义的,即
a
1
+ a
2
=
a
11
+ a
12
a
21
+ a
22
.
.
.
a
n1
+ a
n2
, λa
1
=
λa
11
λa
21
.
.
.
λa
n1
在这种符号体系下,我们把 D 重写成
D =
a
11
a
12
··· a
1n
a
21
a
22
··· a
2n
.
.
.
.
.
.
.
.
.
.
.
.
a
n1
a
n2
··· a
nn
= det(a
1
, a
2
, ··· , a
n
)
一般来说,当我们对于某一问题或某一事物由表及里作深入探讨时,要点在于精益求精地掌握其
本质和精要所在,所以在进一步研讨行列式时,我们的中心课题就是要对于行列式的各种各样性
质作系统的整理。行列式的两个基本性质在于其斜对称性和多线性。由行列式的定义式2.17易见
它对于第一列是线性 (linear) 的,即:
det(λa
1
+ µa
∗
1
, a
2
, ··· , a
n
) =
n
X
i=1
(−1)
i+j
(λa
i1
+ µa
∗
i1
)D
i,j
= λ det(a
1
, a
2
, ··· , a
n
) + ··· + µ det(a
∗
1
, a
2
, ··· , a
n
)
运用斜对称性,就可以把线性条件推广到其他各列,例如第二列:
det(a
1
, λa
2
+ µa
∗
2
, ··· , a
n
) = det(λa
2
+ µa
∗
2
, a
1
, ··· , a
n
)
= −λ det(a
2
, a
1
, ··· , a
n
) − µ det(a
∗
2
, a
1
, ··· , a
n
)
= λ det(a
1
, a
2
, ··· , a
n
) + µ det(a
1
, a
∗
2
, ··· , a
n
)
上述对于每一列都是线性的特性称为多线性 (multilinear),一般有下述定义:
25

3.1 斜对称多线性函数与行列式的界定定理
定义3.1 多线性函数: 设 f(x
1
, x
2
, ··· , x
n
) 为一个以向量为变量的多元函数。若对于每一个
j(1 ≤ j ≤ n),当 x
1
, ··· , x
j−1
, x
j+1
, ··· , x
n
,全部固定不动时 f 恒为 x
j
的线性函数,则称 f
为多线性函数。
现在我们证明下述定理,它说明了斜对称性和多线性两者基本上已经界定了行列式的基本性质,
也就是说行列式就是 n 个列向量的斜对称多线性函数。
定理 3.1. 行列式界定定理
设 f(a
1
, a
2
, ··· , a
n
) 为一个含有 n 维向量变量的函数,并满足斜对称性和多线性,则
f(a
1
, a
2
, ··· , a
n
) = f(e
1
, e
2
, ··· , e
n
) · det(a
1
, a
2
, ··· , a
n
) (3.1)
证明. 要证上述定理,即是证下式成立
f(a
1
, a
2
, ··· , a
n
) − f(e
1
, e
2
, ··· , e
n
) · det(a
1
, a
2
, ··· , a
n
) = 0
令
F (a
1
, a
2
, ··· , a
n
) = f(a
1
, a
2
, ··· , a
n
) − f(e
1
, e
2
, ··· , e
n
) · det(a
1
, a
2
, ··· , a
n
)
易见 F (a
1
, a
2
, ··· , a
n
) 也满足斜对称性和多线性,而且 F (e
1
, e
2
, ··· , e
n
) = 0。我们要用这三
点已知条件推论 F (a
1
, a
2
, ··· , a
n
) ≡ 0。
我们可以用标准基底列向量,把每个 a
j
写成它们的线性组合,即:
a
1
= a
11
e
1
+ a
21
e
2
+ ··· + a
n1
e
n
=
n
X
i
1
=1
a
i
1
1
e
i
1
a
2
= a
12
e
1
+ a
22
e
2
+ ··· + a
n2
e
n
=
n
X
i
2
=1
a
i
2
2
e
i
2
···
a
n
= a
1n
e
1
+ a
2n
e
2
+ ··· + a
nn
e
n
=
n
X
i
n
=1
a
i
n
n
e
i
n
运用 F 的多线性,逐步把 F 展开如下:
F (a
1
, a
2
, ··· , a
n
) = F (
n
X
i
1
=1
a
i
1
1
e
i
1
,
n
X
i
2
=1
a
i
2
2
e
i
2
, ··· ,
n
X
i
n
=1
a
i
n
n
e
i
n
)
=
n
X
i
1
=1
a
i
1
1
F (e
i
1
,
n
X
i
2
=1
a
i
2
2
e
i
2
, ··· ,
n
X
i
n
=1
a
i
n
n
e
i
n
)
=
n
X
i
1
=1
a
i
1
1
n
X
i
2
=1
a
i
2
2
F (e
i
1
, e
i
2
, ··· ,
n
X
i
n
=1
a
i
n
n
e
i
n
)
.
.
.
=
n
X
i
1
=1
a
i
1
1
n
X
i
2
=1
a
i
2
2
···
n
X
i
n
=1
a
i
n
n
F (e
i
1
, e
i
2
, ··· , e
i
n
) (1)
上述 (1) 式有 n
n
个展开项,但每一个展开项都是 0,加总之后还是 0。理由如下:
1. 当下标 (i
1
, i
2
, ··· , i
n
) 之中有任何两个相同时,则由 F 的斜对称性可知
F (e
i
1
, e
i
2
, ··· , e
i
n
) = −F (e
i
1
, e
i
2
, ··· , e
i
n
)
因此,F (e
i
1
, e
i
2
, ··· , e
i
n
) 的值必为 0。
2. 当 n 个下标都相异时,由其斜对称性可得 F (e
i
1
, e
i
2
, ··· , e
i
n
) = ±F (e
1
, e
2
, ··· , e
n
) = 0。
26

3.2 行列式的几何意义——LEIBNIZ FORMULA
行列式界定定理说明了,不管一个函数如何定义,只要它满足斜对称性和多线性,其函数
值一定等于 f(e
1
, e
2
, ··· , e
n
) · det(a
1
, a
2
, ··· , a
n
) = 0。若 f(e
1
, e
2
, ··· , e
n
) 的值已经给
定,那么满足斜对称性和多重线性的函数是唯一的。特别地,若 f(e
1
, e
2
, ··· , e
n
) = 1,该
函数就是行列式。由此可见,斜对称性和多线性已经决定了行列式的全部性质。
有些教材将行列式界定定理以及 f (e
1
, e
2
, ··· , e
n
) = 1 条件称为行列式公理定义,而不是
给出行列式的计算公式作为其定义。这是因为,我们仅凭斜对称性和多线性就可以推导出
行列式的计算公式,这可以参考3.2节:Leibniz formula。
3.2 行列式的几何意义——Leibniz formula
一个 n × n 阶矩阵 A = [a
ij
] 的行列式存在多种不同的定义方式,目前最被广泛采用的定义当属
莱布尼兹 (Gottfried Wilhelm Leibniz) 公式:
det A =
X
p
σ(p)a
p
1
1
a
p
2
2
···a
p
n
n
其中 p = (p
1
, p
2
, . . . , p
n
) 是数组 (1, 2, . . . , n) 的排列 (permutation,或称置换),总共有 n! 种可
能。函数 σ(p) 是排列 p 的符号差 (sign) 或称签名 (signature)。任何一个排列 p 可以分解成换
位 (transposition) 的复合运算,例如,p = (3, 5, 1, 2, 4) 的换位分解是 (1, 3) ◦ (2, 4) ◦ (2, 5),排
列 p 至自然排序 (1, 2, 3, 4, 5) 的换位过程如下:
(3, 5, 1, 2, 4)
(2,5)
−−−→ (3, 4, 1, 2, 5)
(2,4)
−−−→ (3, 2, 1, 4, 5)
(1,3)
−−−→ (1, 2, 3, 4, 5)
我们定义 σ(p) = 1 若 p 包含偶数个换位,σ(p) = −1 若 p 包含奇数个换位。下文从行列式的几
何定义出发,解说如何从三个设定的性质推导出莱布尼兹行列式公式。
推导莱布尼兹公式
将 n ×n 阶矩阵 A 以列向量 (column vector) 表示为 A =
a
1
a
2
··· a
n
。若 n = 2,以平面
上二维向量 a
1
和 a
2
当作交于原点的两边可定义一个平行四边形。若 n = 3,以空间中三维向
量 a
1
, a
2
, a
3
当作交于原点的三边可定义一个平行六面体。推广至有限维空间 R
n
,a
1
, a
2
, . . . , a
n
也定义了一个平行多面体,其体积记为 f(a
1
, a
2
, . . . , a
n
)。
如果 f (a
1
, . . . , a
n
) = 0,矩阵 A 对应的平行多面体称为退化 (degenerate)。如果存在 n 个连续
函数 a
1
(t), . . . , a
n
(t) 使得每一 a
i
(0) = a
i
,a
i
(1) = e
i
(这里 e
i
表示第 i 元等于 1,其余元为 0
的单位向量),而且 f(a
1
(t), . . . , a
n
(t)) 6= 0,0 ≤ t ≤ 1,我们说 A 是正向 (positively oriented),
否则称为负向 (negatively oriented)。换句话说,平行多面体的体积有正负号,f(a
1
, . . . , a
n
) > 0
若 A 是正向,f(a
1
, . . . , a
n
) < 0 若 A 是负向。
根据欧式几何学知识,我们有底下三个关于平行多面体体积的基本性质:
性质一:f(e
1
, e
2
, . . . , e
n
) = 1
性质二
1
:f(a
1
, a
2
, . . . , a
n
) = 0,若存在 a
i
= a
j
,且 i 6= j
性质三
2
:对于任意 i = 1, . . . , n 和常数 k,
f(a
1
, . . . , a
i
+ a
′
i
, . . . , a
n
) = f(a
1
, . . . , a
i
, . . . , a
n
) + f(a
1
, . . . , a
′
i
, . . . , a
n
)
f(a
1
, . . . , ka
i
, . . . , a
n
) = kf(a
1
, . . . , a
i
, . . . , a
n
).
1
即上文提到的交错性
2
即线性。准确来说,应该称为多线性。
27

3.2 行列式的几何意义——LEIBNIZ FORMULA
性质一称为归一性 (normalization),无须进一步讨论。性质二说明两个相同的重合向量造成平行
多面体退化。性质三表示 f 是一个多重线性 (multilinear) 函数,意思是当所有 a
j
固定时 (j 6= i),
f 是 a
i
的线性函数。具体来说,性质三抽象了欧氏空间的性质:全等性和可剖分性。使用退化
和多重线性函数性质可推演出性质四:f 是一个斜对称函数。
在推导莱布尼兹公式前,我们先利用性质二、性质三推导出性质四(斜对称性)。
性质四:对于任意 i 6= j,交换 a
i
和 a
j
改变 f 的正负号,即
f(a
1
, . . . , a
i
, . . . , a
j
, . . . , a
n
) = −f(a
1
, . . . , a
j
, . . . , a
i
, . . . , a
n
)
证明. 因为仅有第 i 和 j 个指标改变,为了方便,我们采用简写
f(u, v) = f(a
1
, . . . , a
i
, . . . , a
j
, . . . , a
n
)
其中 u = a
i
且 v = a
j
使用性质二和三,可得
f(u, v) = f(u, u) + f( u, v)
= f (u, u + v)
= f (u, u + v) − f (u + v, u + v)
= f (−v, u + v)
= −f (v, u + v)
= −f (v, u) − f(v, v)
= −f (v, u).
定义 det A = f(a
1
, . . . , a
n
),现在开始推导莱布尼兹公式。将行向量 a
j
表示为标准基底向量
{e
1
, . . . , e
n
} 的线性组合:
a
j
=
a
1j
.
.
.
a
nj
= a
1j
e
1
+ ··· + a
nj
e
n
=
n
X
i=1
a
ij
e
i
, j = 1, . . . , n
使用性质三,对于 j = 1,写出
f(a
1
, a
2
, . . . , a
n
) = f
n
X
i=1
a
i1
e
i
, a
2
, . . . , a
n
!
=
n
X
i=1
a
i1
f(e
i
, a
2
, . . . , a
n
).
对于 j = 2,继续可得
f(a
1
, a
2
, . . . , a
n
) =
n
X
i=1
n
X
k=1
a
i1
a
k2
f(e
i
, e
k
, . . . , a
n
)
重复此程序 n 次,结果如下:
f(a
1
, a
2
, . . . , a
n
) =
X
ρ
a
ρ
1
1
a
ρ
2
2
···a
ρ
n
n
f(e
ρ
1
, e
ρ
2
, . . . , e
ρ
n
)
其中 ρ = (ρ
1
, . . . , ρ
n
) 且每一 ρ
i
∈ {1, 2, . . . , n},因此共有 n
n
种组合。如果 ρ 不是一个排列,则
存在 i 6= j 使得 ρ
i
= ρ
j
,那么根据性质二,f(e
ρ
1
, e
ρ
2
, . . . , e
ρ
n
) = 0。这表示我们仅需要针对所
有可能的排列 p 加总即可:
f(a
1
, a
2
, . . . , a
n
) =
X
p
a
p
1
1
a
p
2
2
···a
p
n
n
f(e
p
1
, e
p
2
, . . . , e
p
n
)
28
3.3 标量面积
使用性质四,f 是一个斜对称函数。若排列 p 分解成 k 个换位,则 σ(p) = (−1)
k
。所以,对于
任一排列 p:
f(e
p
1
, e
p
2
, . . . , e
p
n
) = σ(p)f(e
1
, e
2
, . . . , e
n
)
合并以上结果并使用性质一,便得到平行多面体体积算式:
f(a
1
, a
2
, . . . , a
n
) =
X
p
σ(p)a
p
1
1
a
p
2
2
···a
p
n
n
此即莱布尼兹行列式公式。
有向体积是具有多线性和斜对称性的函数,根据行列式界定定理,这样的函数是唯一的(或者只
相差一个系数)。因此,有向体积和行列式本质上是相同的。因为 f(e
1
, e
2
, . . . , e
n
) = 1,所以:
f(a
1
, a
2
, . . . , a
n
) = det(a
1
, a
2
, . . . , a
n
)
莱布尼兹公式从行列式的两个基本性质(斜对称性和多线性)出发,推导出了行列式的 n! 项展
开式。但莱布尼兹公式还有一个问题没有解决,即如何确定每一项的正负号?在3.4节,我们将
通过排列的逆序数来解决这个问题。
3.3 标量面积
上一节叙述了有向面积的推导,但我们更常见的可能是标量面积。显然,有向面积和标量面积的
前提假设是不一样的,有向面积具有斜对称性,而标量面积符合对称性。下面简述标量面积公式
的推导过程,虽然这与代数无关,但以此与有向面积作对比。至于为什么有向面积的绝对值和标
量面积具有等价性,仍是疑问。
面积是表示图形大小的度量。早在几千年前,古人已经开始探索面积的计算公式。在公元前 1700
年前,古巴比伦人留下的泥板书中,记录了大量的数学问题,其中就包括面积、体积的计算。古
人对面积的思考并不是来自于抽象或虚无缥缈的想法,而是来自社会实践。
在农耕文明时代,开始出现私有财产,人们需要一些度量手段用以划分土地。有研究表明,在古
埃及,在尼罗河每年泛滥之后,古埃及人需要使用规则的形状来重新划分土地。那时,古埃及人
就发现利用规则图形的全等性,有助于计算土地面积。古代的中国也是典型的农耕文明社会,农
田面积的计算非常重要,不仅关系到如何分配土地、还关系到如何收税。在《九章算术》的第一
卷方田的第一、二题就给出了矩形面积的计算方法。可见,在古代,面积最重要的应用就是计算
土地面积,这也激发了古人对面积问题的思考。
在不断的社会实践中,人们发现用分割法来计算土地面积比较方便。例如,一个矩形等于多个小
矩形面积之和,圆的面积可以使用多个三角形或者正六边形的面积之和来近似等等。基于分割
法的思想,我们可以先定义一种简单图形的面积,再拼接多个简单图形去近似其他图形的面积。
这不仅是古人计算图形面积的思想,也是现代数学计算图形面积的思想。
那么要选择哪种几何图形作为度量面积的基础呢?因为我们需要使用这种简单的图形以及分割
法去度量其他图形的面积,这就要求这种简单的封闭图形可以密铺一个平面。容易想象,边数最
少的可密铺封闭图形是三角形,其次是矩形/平行四边形/梯形。矩形由两个直角三角形构成,而
平行四边形和梯形可以用矩阵和三角形分割,因此,我们只需要定义矩形的面积。
从现代数学的角度来看,面积/体积是 Lebesgue 测度,或者说面积是由 Lebesgue 测度定义的。
这似乎暗示着要理解面积的定义需要先学习测度论。实际上不必如此,测度论诞生于 20 世纪,
历史上,先有面积而后有测度论,测度论只是为了完备已有数学理论而提出的。如果面积符合如
下几个朴素的要求,我们就可以推导出矩形面积的计算公式。
1. 相同/全等的图形面积应该都相等。例如:长和宽对应相等的长方形是全等的,所以面积是
长和宽的函数 f (a, b)。这里不限定长和宽的大小关系,那么得到了对称性:f(a, b) = f(b, a)。
2. 面积应当是非负函数,不存在面积为负的情况,边长不为 0 时面积不为 0。
29
3.4 行列式的逆序式定义
3. 几个无重叠图形的总面积应该是各个图形的面积之和。对于长相等的长方形,将它们对齐长
边,把宽边拼在一起,可以形成另一个长方形,宽是两者之和,这意味着可加性:f (a
1
+a
2
, b) =
f(a
1
, b) + f(a
2
, b);特别地,如果两个矩阵全等,则面积之和是单个矩阵面积的两倍,这意
味着齐次性:f(2a, b) = 2 f (a, b)。可加性和齐次性统称为多线性。
从上面三条性质还可以推导出另一条比较重要的性质:
4. 如果一个图形 A 能够完全覆盖另一个图形 B,那么 A 的面积应该比 B 的大。这也就是单
调性,面积关于边长单调递增。
当矩形的边长 a, b 为正整数时,根据多线性,可以得到矩形面积计算公式:
f(a, b) = f(
a
X
i
1,
b
X
i
1) =
a
X
i
f(1, b · 1) =
a
X
i
b
X
i
f(1, 1) = abf (1 , 1)
可以看出面积函数 f (a, b) 必须是 ab 的常数倍,为了使用方便,不妨规定边长为 1 的正方形作
为单位面积图形,即 f(1, 1) = 1,然后用这个单位面积去丈量其他图形,那么边长为整数 a, b 的
矩形面积则为 ab。
5. 如果一个矩形的边长 a, b 不是整数,而是其他非负有理数,例如 a = x/p, b = y/q,其中
x, y, p, q 为正整数。因为有理数可以表示为两个整数之比,显然矩形面积的多线性可以推
广到有理数域。e.g. 把单位正方形的一个边均分成 p 段,另一边均分为 q 段,则单位正方
形正好是 pq 个边长分别为 1/p, 1/q 的小矩形构成,则边长为 a, b 的矩形面积应该 ab。即
对于非负有理数,有 qf (a, b) = f(qa, b),上述矩形面积公式任然成立。
6. 当边长 a, b 是一般实数时,因为任意实数都可以用有理数数列进行逼近,所以矩形面积公
式对于实数也成立。
7. f 关于 a 连续(即证明 f (a, b) 在 a 趋向于 0 时右极限为 0,首先单调递减有下界所以极
限一定存在,其次用第三个描述说明 f(a, b) 可以任意接近于 0,因此极限为 0)
虽然,我们对面积函数有几个朴素的要求,但矩形面积的计算公式只根据多线性就可以推导出
来。而多线性实际上体现了欧式空间的全等性和可剖分性,前者体现了欧氏空间中可平移、旋转
和反射而不变的性质,后者表示“长宽分别为 a, b 倍的矩形 A 可以剖分为 ab 个矩形 B”。
在很多情况下,面积或测度可以被人为是积分,但实际上积分只是计算面积的公式,这是 Radon-
Nikodym 定理的内容。
容易发现,标量面积是以实数为因变量,而有向面积以向量作为因变量。有向面积函数的因变量
交换次序,面积的方向改变,但并不会影响因变量维度的次序,因变量向量还是原来的向量。而
标量面积的因变量交换次序,在几何的角度上看,因变量的维度也已经改变,如下图。对应到行
列式,相当于即交换两行,又交换两列,因此不变号。从这个角度上看,标量面积和有向面积得
到统一。
注意 f(a, b) = f (b, a) 含义:原来 a 为长,b 为宽,变为 b 为长,a 为宽。
用行列式表示就是
a 0
0 b
=⇒
0 b
a 0
=⇒
b 0
0 a
这个变换经历了两次行列交换操作,所以符号反转两次,符号不变。
3.4 行列式的逆序式定义
30
3.4 行列式的逆序式定义
图 3.1: 面积函数的对称性
3.4.1 排列与逆序数
定义3.2 排列: 由 n 个数字 1, 2, 3, ··· , n 组成一个有序数组 (j
1
, j
2
, ··· , j
n
) 称为一个 n 级排列,
其中 j
1
表示排列的第 1 个数,j
2
表示排列的第 2 个数,j
n
表示排列的第 n 个数。
定义3.3 逆序: 在一个 n 级排列中, 如果某个较大的数排在某个较小的数的前面,则称这两个数
构成该排列的一个逆序。
定义3.4 逆序数: 一个排列中逆序的总数称为该排列的逆序数。排列 (j
1
, j
2
, ··· , j
n
) 的逆序数记
为 τ(j
1
, j
2
, ··· , j
n
)。
定义3.5 奇排列、偶排列: 称逆序数为奇数的排列为奇排列,逆序数为偶数的排列为偶排列。
定义3.6 对换: 将一个排列中某两个元素的位置对调,而其余的数不动,就得到一个新排列,这
样的一个变换称为一次对换。
定理 3.2
对换一次改变排列的奇偶性。
证明. (1) 对换的两数相邻。设原排列为
(A, i, j, B)
其中 A, B 表示排列中除 i, j 以外的其余数,经过对换 (i, j) 变为新排列
(A, j, i, B)
比较两个排列中的元素的次序可知,A, B 中的数的次序没有改变,并且 i, j 与 A, B 中数的次序
也没有改变,仅改变了 i 与 j 的次序。同时,新排列仅原排列增加 ( 当 i < j 时 ) 或减少 ( 当
i > j 时 ) 一个次序,所以它们的奇偶性相反。
(2) 再证一般的情况。设原排列为
(A, i, c
1
, c
2
, ··· , c
t
, j, B)
经过对换 (i, j),变为新排列
(A, j, c
1
, c
2
, ··· , c
t
, i, B)
因为将原排列中的 i 依次与 c
1
, c
2
, ··· , c
t
, j 作 t + 1 次相邻对换,得到排列
(A, c
1
, c
2
, ··· , c
t
, j, i, B)
31

3.4 行列式的逆序式定义
再将 j 依次与 c
t
, ··· , c
2
, c
1
作 t 次相邻对换,得到排列
(A, j, c
1
, c
2
, ··· , c
t
, i, B)
因此,原排列经过 2t + 1 次相邻的对换即得到新排列,而 2t + 1 为奇数,所以新、旧排列的奇
偶性相反。
推断 3.2-1 在全部 n(n ≥ 2) 级排列中, 奇排列、偶排列的个数相等, 各为
n!
2
.
证明. 证明也简单,用反证法。假设在全部 n 元排列中,有 s 个奇排列,有 t 个偶排列。现在
假设,奇、偶排列个数不相等,例如奇排列个数 > 偶排列个数。那么,将 s 个奇排列前面两个
数对换,则得到 s 个偶排列;将 t 个偶排列前面两个数对换,则得到 t 个奇排列。对换前,有
s > t;对换后有 t > s。显然矛盾,原假设不成立。
定理 3.3
任意一个 n 级排列与排列 12 ···n 都可以经过一系列对换互变,并且所作对换的个数与这
个排列有相同的奇偶性。
证明. * 使用数学归纳法。
1 1 级排列只有一个,结论显然成立。
2 假设结论对
n
−
1
级排列已经成立。
3
现在来证对 n 级排列的情形结论也成立。设 j
1
j
2
···j
n
是一个 n 级排列,如果 j
n
= n,那么
根据归纳法假设,n − 1 级排列 j
1
j
2
···j
n−1
可以经过一系列对换变成 12 ···n − 1,于是这一系
列对换也就把 j
1
j
2
···j
n
变成 12 ···n。此时,结论对 n − 1 级排列成立。
如果 j
n
6= n,那么先对 j
1
j
2
···j
n
作 j
n
, n 对换,它就变成 j
′
1
···j
′
n−1
n,这就归结成上面的情形。
因为 j
′
1
···j
′
n−1
n 与 j
′
1
···j
′
n−1
有相同的逆序数,因此结论普遍成立。相仿地 , 1, 2, ··· , n 也可用
一系列对换变成 j
1
j
2
···j
n
,因为 12 ···n 是偶排列,所以根据定理3.2,所作对换的个数与排列
j
1
j
2
··· j
n
有相同的奇偶性。
3.4.2 n 阶行列式的逆序数定义
定义3.7 n 阶行列式: 将 n
2
个数 a
ij
(i, j = 1, 2, ··· , n) 组成的记号
D =
a
11
a
12
··· a
1n
a
21
a
22
··· a
2n
.
.
.
.
.
.
.
.
.
.
.
.
a
n1
a
n2
··· a
nn
.
称为 n 阶行列式, D 等于取自不同行不同列的 n 个元素乘积的代数和,即:
D =
X
j
1
j
2
···j
n
(−1)
τ (j
1
,j
2
,···,j
n
)
a
1j
1
a
2j
2
. . . a
nj
n
其中 (j
1
, j
2
, ··· , j
n
) 是一个 n 级排列,
P
是对所有的 n 级排列求和,τ (j
1
, j
2
, ··· , j
n
) 是 n 级
排列的逆序数。
由定义可知,由于 (j
1
, j
2
, ··· , j
n
) 为一个 n 级排列,而这样的排列共有 n! 个,因此 n 阶行列式
D 是 n! 项的代数和;和式中的每一项是取自 D 中位于不同行不同列的个 n 元素的乘积; 当排
列 (j
1
, j
2
, ··· , j
n
) 为偶排列时该项带正号,奇排列时带负号。
32
3.5 对比行列式的三种定义
3.5 对比行列式的三种定义
以上三种行列式的定义都是等价的,因为它们都可以导出行列式具有斜对称性和多线性,而这两
个基本性质决定了行列式的所有其他性质。这三种定义方式各有特点,递归定义是行列式被发
现时的原始模样,揭示了高斯消元法与行列式的关系;莱布尼兹公式将行列式与几何相结合,揭
示了平行多面体的有向体积就是行列式;排列式的定义虽然十分突兀,但形式上和莱布尼兹公式
是一致的,且给出了每一项的正负号,在一定程度上让行列式的各种性质更易于证明。
相信任何人都会认同递归定义最自然地引出了行列式这个概念。在进行递归定义时,先是有了
交错性、斜对称性这两个性质,再利用斜对称性和归纳法证明快速消元法在 n 等于任意正整数
时皆成立,由此得到行列式的递归定义。最后从递归定义推导出行列式具有多线性。
莱布尼兹公式从体积函数的三个原始假设(归一性、交错性、多线性)出发,先是推导出斜对称
性,而后再利用斜对称性和多线性推导出行列式的计算公式,该计算公式形式上和行列式的排列
式定义是一致的。
基于以上两种定义,数学家们已经知道行列式的计算公式,因此基于排列和逆序数,可以直接写
出 n 阶行列式的展开式。基于此展开式又可推导出行列式的基本性质。
3.6 行与列的对称地位
使用递归定义证明行列对称
前面提到,行列式源于 n 阶线性方程组和 n 维平行多面体有向体积,由此易见它的 n
2
个变元是
自然而然地具有行、列的编排的(这也就是行列式这个名称的来由)。因此,在行列式基本性质
的研讨中,自然应该把每一列(或每一行)的 n 个变元看成一个整体。我们將用 x
j
, 1 ≤ j ≤ n,
表示 j 列向量;¯x
i
, 1 ≤ i ≤ n,表示行向量,亦即
x
j
=
x
1j
x
2j
.
.
.
x
nj
¯
x
i
= (x
i1
, x
i2
, ··· , x
im
)
在前面的讨论中,我们把行列式看成其 n 个列向量的函数,即 det(x
1
, x
2
, ··· , x
n
)。由行列式的
界定定理可见,下述三点业已构成行列式的一组特征性质:
1. 斜对称性:det(··· , x
i
, ··· , x
j
, ···) = −det(··· , x
j
, ··· , x
i
···)
2. 多线性:det(x
1
, ··· , λx
i
+ µy
i
, ··· , x
n
) = λ det(x
1
, ··· , x
i
, ··· , x
n
) +
µ det(x
1
, ··· , y
i
, ··· , x
n
)
3. det(e
1
, e
2
, ··· , e
n
) = 1
当然也可以把行列式看作 n 个行向量 {
¯
x
1
,
¯
x
2
, ··· ,
¯
x
n
} 的多项式函数,记为 f (
¯
x
1
,
¯
x
2
, ··· ,
¯
x
n
)。
我们很自然要问它是否也同样地具有上述三点基本性质?假如具有,则 f(
¯
x
1
,
¯
x
2
, ··· ,
¯
x
n
) =
det (
¯
x
1
,
¯
x
2
, ··· ,
¯
x
n
)。换言之,亦即行列式是否具有在 x
ij
↔ x
ji
互换之下保持不变的行、列对
称性?不难看到,在 n = 1, 2, 3 的情形是具有这种行、列互换,保特不变的对称性。由此,我们
当然又会想到用归纳法去研讨它是否普遍成立?由前面的经验可见,我们只要能够验证行列式
也可以对于其第一行有下述展开公式,即
D = |x
ij
|
?
=
n
X
j=1
(−1)
j+1
x
1j
D
1,j
(3.2)
假若上式得证,则可用完全同样的结论,归纳地证明 f(
¯
x
1
,
¯
x
2
, ··· ,
¯
x
n
) 的斜对称性和多线性,而
f(
¯
e
1
,
¯
e
2
, ··· ,
¯
e
n
) = 1 是显然的。兹证明式如下:
33

3.6 行与列的对称地位
证明. 我们要用已知的递归定义式2.17推导出行列式也可以按首行展开。设 |a
ij
| 6= 0,由行列式
的斜对称性和2.17式可得 (这里用到了行列式可按任意一列展开的性质,具体可参考3.8节)
det(a
1
, ··· , a
j−1
, e
1
, a
j+1
, a
n
) = (−1)
j+1
D
1,j
由 Cramer 法则可知,方程组2.18是否有唯一解只取决于其系数矩阵的行列式是否为 0,与 b 无
关。因此,我们可以令 b 为任意值。由方程组2.18在 b = e
1
时的唯一解公式,即有
x
j
=
1
D
det(··· , e
1
, ···) =
1
D
(−1)
j+1
D
1,j
将它代入2.16的第一式,即有
n
X
j=1
a
1j
x
j
=
1
D
n
X
j=1
(−1)
j+1
a
1j
D
1,j
= 1
即
n
X
j=1
(−1)
j+1
a
1j
D
1,j
= D
对于任给 |a
ij
| 6= 0 的取值恒成立。因此3.2式仍是 n
2
变元的恒等式。
推断 3.3-1 行列式对于行向量也有同样的斜对称性和多线性。再者,它也有下述对于第 i 行的
展开式
D = |x
ij
| =
n
X
j=1
(−1)
j+1
a
1j
D
1,j
使用逆序式定义证明行列对称
在行列式的逆序数定义3.7中,为了决定每一项的正负号,我们把 n 个元素按行指标排起来。事
实上,数的乘法是交换的,因而这 n 个元素的次序是可以任意写的,一般地, n 级行列式中的项
可以写成
a
i
1
j
1
a
i
2
j
2
···a
i
n
j
n
(1)
其中,i
1
i
2
···i
n
和 j
1
j
2
···j
n
是两个 n 级排列。为了根据定义3.7来决定 (1) 的符号,就要把这
n 个元素重新排一下使得它们的行指标成自然顺序,也就是排成
a
1j
′
1
a
2j
2
···a
nj
′
n
(2)
于是它的符号是
(−1)
τ
(
j
′
1
j
′
2
···j
′
n
)
(3)
事实上,利用排列的性质,不难证明,(1) 的符号等于
(−1)
τ (i
1
i
2
···i
n
)+τ (j
1
j
2
···j
n
)
(4)
现在来证明,(3) 与 (4) 是一致的。我们知道,由 (1) 变到 (2) 可以经过一系列元素的对换来实
现。每作一次对换,元素的行指标与列指标所成的排列 i
1
i
2
···i
n
与 j
1
j
2
···j
n
就都同时作一次
对换,也就是 τ (i
1
i
2
···i
n
) 与 τ (j
1
j
2
···j
n
) 同时改变奇偶性,因而它们的和
τ (i
1
i
2
···i
n
) + τ (j
1
j
2
···j
n
)
34

3.7 行列式的性质
的奇偶性不改变。这就是说,对 (1) 作一次元素的对换不改变 (4) 的值。因此,在一系列对换之
后有
(−1)
τ (i
1
i
2
···i
n
)+τ (j
1
j
2
···j
n
)
= (−1)
τ (12···n)+τ
(
j
′
1
j
′
2
···j
′
n
)
= (−1)
τ
(
j
′
1
j
′
2
···j
′
n
)
这就证明了 (3) 与 (4) 是一致的。按 (4) 来决定行列式中每一项的符号的好处在于,行指标与列
指标的地位是对称的,因而为了决定每一项的符号,我们同样可以把每一项按列指标排起来,于
是定义3.7又可写成
a
11
a
12
··· a
1n
a
21
a
22
··· a
2
n
.
.
.
.
.
.
.
.
.
.
.
.
a
n1
a
n2
··· a
nn
=
X
i
1
i
2
···i
n
(−1)
τ (i
1
,i
2
,···,i
n
)
a
i
1
1
a
i
2
2
. . . a
i
n
n
由此,立即可以推导出:将行列式的行列互换,不会改变行列式的值,即行列式转置,值不变。
另外,这也表明对行成立的性质,对列也成立。
3.7 行列式的性质
这一节讲述行列式的性质,这里会从两个角度来理解同一个内容:一是 n 阶行列式展开式的角
度,二是莱布尼兹公式的角度,也就是几何体积的角度。
3.7.1 行列式展开式的角度
定义3.8 转置行列式: 记
D =
a
11
a
12
··· a
1n
a
21
a
22
··· a
2n
.
.
.
.
.
.
.
.
.
.
.
.
a
n1
a
n2
··· a
nn
, D
T
=
a
11
a
21
··· a
n1
a
12
a
22
··· a
n2
.
.
.
.
.
.
.
.
.
.
.
.
a
1n
a
2n
··· a
nn
D
T
为行列式 D 的转置行列式, 转置行列式也可记为 D
′
.
性质 1
行列互换,行列式不变。即行列式与它的转置行列式相等,D
T
= D.
性质 2:齐次性
行列式一行或一列的公因子可以提到行列式外面,或者说用一个数乘行列式的一行(列)
相当于用这个数乘此行列式,即:
a
11
a
12
··· a
1n
.
.
.
.
.
.
.
.
.
.
.
.
ka
i1
ka
i2
··· ka
in
.
.
.
.
.
.
.
.
.
.
.
.
a
n1
a
n2
··· a
nn
= k
a
11
a
12
··· a
1n
.
.
.
.
.
.
.
.
.
.
.
.
a
i1
a
i2
··· a
in
.
.
.
.
.
.
.
.
.
.
.
.
a
n1
a
n2
··· a
nn
.
推断 3.3-2 行列式中某一行(列)为零,则行列式为零。
35
3.7 行列式的性质
性质 3: 可加性
若行列式某一行 ( 列 ) 的元素都是两数之和,则该行列式为下列两个行列式的和。而这两
个行列式除这一行(列)以外全与原来行列式的对应的行(列)一样。
例如第 i 行元素都是两数之和:
a
11
a
12
··· a
1n
.
.
.
.
.
.
.
.
.
.
.
.
a
i1
+ b
i1
a
i2
+ b
i2
··· a
in
+ b
in
.
.
.
.
.
.
.
.
.
.
.
.
a
n1
a
n2
··· a
nn
=
a
11
a
12
··· a
1n
.
.
.
.
.
.
.
.
.
.
.
.
a
i1
a
i2
··· a
in
.
.
.
.
.
.
.
.
.
.
.
.
a
n1
a
n2
··· a
nn
+
a
11
a
12
··· a
1n
.
.
.
.
.
.
.
.
.
.
.
.
b
i1
b
i2
··· b
in
.
.
.
.
.
.
.
.
.
.
.
.
a
n1
a
n2
··· a
nn
性质 4: 交错性
如果行列式中有两行(列)相等,那么行列式为零。
证明. 设行列式
a
11
a
12
··· a
1n
.
.
.
.
.
.
.
.
.
a
i1
a
i2
··· a
in
.
.
.
.
.
.
.
.
.
a
k1
a
k2
··· a
kn
.
.
.
.
.
.
.
.
.
a
n1
a
n2
··· a
nn
=
X
j
1
···j
n
(−1)
τ (j
1
···j
i
···j
k
···j
n
)
a
1j
1
···a
ij
i
···a
kj
k
···a
nj
n
(1)
中第 i 行与第 k 行相同,即
a
ij
= a
kj
, j = 1, 2, ··· , n (2)
为了证明 (1) 为零。只需证明 (1) 的右端所出现的项全能两两相消就行了。事实上,与项
(−1)
τ (j
1
···j
i
···j
k
···j
n
)
a
1j
1
···a
ij
i
···a
kj
k
···a
nj
n
同时出现的还有
(−1)
τ (j
1
···j
k
···j
i
···j
n
)
a
1j
1
···a
ij
k
···a
kj
i
···a
nj
n
比较这两项,由 (2) 有
a
ij
i
= a
kj
i
, a
ij
k
= a
kj
k
也就是说,这两项有相同的数值。但是排列
j
1
···j
i
···j
k
···j
n
与j
1
···j
k
···j
i
···j
n
相差一个对换,因而有相反的奇偶性,所以这两项的符号相反。易知,全部 n 级排列可以按上
述形式两两配对。因之,在 (1) 的右端,对于每一项都有一数值相同但符号相反的项与之成对出
现,从而行列式为零。
性质 5
行列式中两行(列)成比例,则行列式为零。
性质 6
把行列式的某一行(列)的倍数加到另一行(列),行列式不变。
36
3.7 行列式的性质
性质 7: 斜对称性/反称性
对换行列式中两行(列)位置,行列式反号。
证明.
6
r
k
− r
i
a
11
a
12
··· a
1n
··· ··· ··· ···
a
i
1
+ a
k1
··· ··· a
in
+ a
kn
··· ··· ··· ···
−a
i1
··· ··· −a
in
··· ··· ··· ···
a
n1
a
n2
··· a
nn
6
r
i
+ r
k
a
11
a
12
··· a
1n
··· ··· ··· ···
a
k1
a
k2
··· a
kn
··· ··· ··· ···
−a
i1
−a
i2
··· −a
in
··· ··· ··· ···
a
n1
a
n2
··· a
nn
a
11
a
12
··· a
1n
··· ··· ··· ···
a
i1
a
i2
··· a
in
··· ··· ··· ···
a
k1
a
k2
··· a
kn
··· ··· ··· ···
a
n1
a
n2
··· a
nn
6
r
i
+ r
k
a
11
a
12
··· a
1n
··· ··· ··· ···
a
i1
+ a
k1
a
2i
+ a
k2
··· a
in
+ a
kn
··· ··· ··· ···
a
k1
a
k2
··· a
kn
··· ··· ··· ···
a
n1
a
n2
··· a
nn
= −
a
11
a
12
··· a
1n
··· ··· ··· ···
a
k1
a
k2
··· a
kn
··· ··· ··· ···
a
i1
a
i2
··· a
in
··· ··· ··· ···
a
n1
a
n2
··· a
nn
3.7.2 几何体积的角度 [wx]
一个矩阵的行列式就是一个平行多面体的 (定向) 体积,这个多面体的边对应矩阵
的行。如果学生们得知了这个秘密 (在纯粹代数式的教学中,这个秘密被小心地隐
藏起来),那么行列式的整个理论将成为多重线性形式理论的一部分。倘若用别的
方式来定义行列式,任何敏感的人都将会永远痛恨诸如行列式、Jacobian 式以及
隐函数定理这些东西。
———俄国数学家阿诺尔德 (Vladimir Arnold)〈论数学教育〉[112 ]
在线性代数发展历史中,行列式和矩阵理论一直有着密切的关系。行列式概念最早出现于解线
性方程组的过程中,十七世纪末,日本数学家关孝和与德国数学家莱布尼茨 (Gottfried Wilhelm
Leibniz) 的著作就已使用行列式来确定线性方程组解的数目与形式。十九世纪以后,矩阵的引入
使得更多的行列式性质被发现,行列式的发展遂渐趋完善。今天多数线性代数教科书都会开辟一
个专门讨论行列式的章节,但主要的目的并非求解线性方程组,而是为了顺利导入矩阵的特征多
项式。不过,美国数学教授阿斯勒 (Sheldon Axler) 却抱持反对的态度,他认为行列式是线性代
数核心原理的推导结果,而不是行列式推导出线性代数的核心原理。1994 年,阿斯勒发表〈断
绝行列式〉( Done with determinants! ),该文严厉抨击行列式目前于线性代数的「地位」,之后
并获得不少数学家的共鸣和回响。阿斯勒反对行列式的理由在于行列式难以理解,不具直觉,而
且常在缺乏明显动机的情况下被引用。不仅如此,行列式与线性代数理论的基调不甚相合。行列
式的计算公式与主要的矩阵运算无关,它像是从一堆矩阵元拼贴出来的蒙太奇,让人困惑如此怪
异的公式究竟是怎么冒出来的。虽然我们无法改变或简化行列式公式,但仍可尝试编排出易于
理解的推导过程。本文从计算平行四边形的面积推导行列式的运算公式,这么做虽有违行列式
诞生的初衷,但此法能够丰富行列式的几何直觉解释并显现行列式的一些重要性质。
设 (a, b) 和 (c, d) 为平面上的两个向量 (见图3.2)。考虑矩阵 A =
a b
c d
,我们定义函数 f (A) =
37

3.7 行列式的性质
f
a b
c d
为 (a, b) 和 (c, d) 所张的平行四边形面积。通常我们会拣选最便捷的解题途径 [见112页],
不过在此我采用一种比较不寻常的作法:先找出此函数必须满足的条件,等待条件充足后,再着
手推导面积函数 f 的公式。
图 3.2: 两个向量张开一个平行四边形
首先考虑最简单情况:(a, b) = (1, 0),(c, d) = (0, 1)。两个垂直的标准单位向量张开单位正方形,
于是有下面的性质。
性质一:f(I) = f
1 0
0 1
= 1,其中 I 是单位矩阵。
再看另一个极端情况:(a, b) = (c, d),两向量完全重合表示所张的平行四边形面积等于零。
性质二 (交错性):若 A 有相同的两列 (row),则 f(A) = 0。
上述两个性质仍不足以规范函数 f ,我们需要更多有关平行四边形的几何性质,特别是所夹向量
改变时,平行四边形面积如何随之变化。图3.3显示向量 (a, b) 的长度伸缩 k 倍,对应的平行四
边形面积亦等比例改变,因此 f 满足下列关系:
f
ka kb
c d
= k · f
a b
c d
图 3.3: 伸缩向量即伸缩平行四边形
从基础几何学可知 (a + a
′
, b + b
′
) 和 (c, d) 所张的平行四边形面积恰为 (a, b) 和 (c, d) 所张的平
行四边形面积与 (a
′
, b
′
) 和 (c, d) 所张的平行四边形面积之和 (见图3.4),亦即
f
a + a
′
b + b
′
c d
= f
a b
c d
+ f
a
′
b
′
c d
运用对称原理,同样也有
f
a b
kc kd
= k · f
a b
c d
f
a b c + c
′
d + d
′
= f
a b
c d
+ f
a b
c
′
d
′
.
我们将上述线性关系合并为一个性质。
性质三 (多线性):考虑 A 的任一列,当其他列都固定时,f(A) 为该列的线性函数。
38
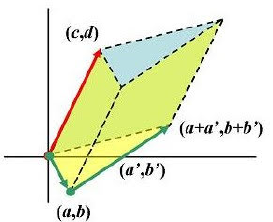
3.7 行列式的性质
图 3.4: 两个平行四边形面积之和等于另一个平行四边形面积
这里要特别强调 f (A) 并非矩阵 A 的线性函数,也就是说,f(kA) = kf(A) 和 f (A + B) =
f(A) + f(B) 不成立。对于 2 × 2 阶矩阵 A,性质三说明
f(kA) = f
ka kb
kc kd
= k · f
a b
kc kd
= k
2
· f
a b
c d
= k
2
f(A).
推广至 n × n 阶矩阵 A,则有 f(kA) = k
n
f(A)。
如果将 A 的两列对调,f(A) 是否改变?交互使用性质二和性质三可以推出下面的结果:
f
a b
c d
= f
a b
a b
+ f
a b
c d
= f
a b
a + c b + d
= f
a b
a + c b + d
− f
a + c b + d
a + c b + d
= f
−c −d
a + c b + d
= −f
c d
a + c b + d
= −f
c d
a b
− f
c d
c d
= −f
c d
a b
.
性质四是性质二和性质三的必然结果。
性质四 (斜对称性):交换 A 的两列改变 f(A) 的正负号。
性质四迫使函数 f(A) 必须是有号 (signed) 或定向 (oriented) 面积。根据性质一,将右手拇指
外的四根手指向手掌弯曲的方向视为由第一列至第二列的旋转方向,则面积为正,反之,面积为
负,此即右手定则。如果最初设定性质一为 f (I) = f
1 0
0 1
= −1,则按左手定则计算有号面
积。另外,假如我们要求平行四边形的面积必须为非负数,f
a b
c d
≥
0
,则性质三不复成立。
我们宁可打破旧有的几何概念接受有号面积,也不愿放弃这个美好的性质:行列式是每一列的线
性函数 (当固定其他列时)。
准备就绪,现在可以利用上述性质推导 f 函数。类似性质四的推演过程,先运用性质三来分解
f,如下:
39
3.7 行列式的性质
f
a b
c d
= f
a 0
c d
+ f
0 b
c d
= f
a 0
0 d
+ f
a 0
c 0
+ f
0 b
c 0
+ f
0 b
0 d
= ad · f
1 0
0 1
+ ac · f
1 0
1 0
+ bc · f
0 1
1 0
+ bd · f
0 1
0 1
.
由性质二可知 f
1 0
1 0
= 0,f
0 1
0 1
= 0,再由性质四和性质一,
f
0 1
1 0
= −f
1 0
0 1
= −1.
合并以上结果,我们导出 f(A) 的计算公式:
f(A) = f
a b
c d
= ad − bc
这就是大家熟知的二阶行列式公式。为方便辨识,我们改以 det A 或 |A| 替代 f (A):
det A =
a b
c d
≜ ad − bc
推导行列式公式的过程虽然使用了性质四,但性质四也是由前面三个性质所导出,所以性质一、
二与三唯一决定行列式的计算公式。沿用上述方法,通过推导空间中平行六面体的体积可得三
阶行列式公式 (见“内积与外积是怎么来的? ”)。稍后我们将以归纳法推演高阶行列式的计算
公式。
接着推演行列式的其他性质。不论前述的四个性质或下面介绍的性质,对任何 n 阶方阵 A 都是
成立的。
性质五:若 A 包含一个零列,则 det A = 0。
以二阶行列式为例,利用性质三,将纯量 0 提出,就有
a b
0 0
= 0
a b
∗ ∗
= 0
性质六:列取代运算,即任一列乘以常数 k 再加进另一列,不改变行列式。
以二阶行列式为例,若第 1 列乘以 k 加进第 2 列,使用性质三和性质二,计算如下:
a b
c + ka d + kb
=
a b
c d
+
a b
ka kb
=
a b
c d
+ k
a b
a b
=
a b
c d
.
性质七:若 A 为三角矩阵,det A 等于主对角元乘积。
假设三角矩阵 A = [a
ij
] 的主对角元皆不含零,以列取代运算将 A 化简为对角矩阵,
D =
a
11
.
.
.
a
nn
性质六指出列取代运算不改变行列式,因此 det A = det D。利用性质三,逐次将 D 的主对角元
提出,再使用性质一,可得
det D = a
11
···a
nn
· det I = a
11
···a
nn
40

3.7 行列式的性质
性质八:若 A 是一个可逆矩阵,则 det A 6= 0;若 A 是不可逆的,则 det A = 0。
对矩阵 A 执行基本列运算,将 A 化简为上三角矩阵 U = [u
ij
],性质四指出列交换运算改变
行列式正负号,性质六则说明列取代运算不改变行列式,因此 det A = ±det U。再由性质七,
det U = u
11
···u
nn
,推论当 A 是可逆时,所有 u
ii
全不为零,故 det A 6= 0 ;当 A 不可逆时,U
必有一个零列,即至少有一 u
ii
= 0,则 det A = 0。
性质九:det(AB) = (det A)(det B)
这可能是最困难证明的一个性质,下面分开两个情况讨论。若 AB 不可逆,则 A 或 B 至少有一
个是不可逆矩阵,性质八给出 det(AB) = 0 = (det A)(det B)。若 A 和 B 都是可逆矩阵,定义
函数
d(A) =
det(AB)
det B
函数 d(A) 满足上述性质一、二和三,因此 d(A) = det A。证明如下:设 A = I,
d(I) =
det(IB)
det B
=
det B
det B
= 1
确定 d(A) 满足性质一。若 A 有相同两列,则 AB 也有相同两列,所以 det( AB) = 0,也就有
d(A) = 0,d(A) 满足性质二。因为 AB 的第 i 列等于 A 的第 i 列乘以 B,对于 A 的任一列的
线性组合,AB 的该列也有同形式的线性组合,故 d(A)� det(AB) 同为该列的线性函数,因此满
足性质三。(其他证明方式请见“利用分块矩阵证明 det(AB) = (detA)(detB)”,“矩阵乘积行列
式公式的代数证法”。)
性质十:det A
T
= det A
如同性质九的证明,下面也分开两个情况讨论。若 A 不可逆,则 A
T
也不可逆,由性质八得知
det A = 0 = det A
T
。若 A 是可逆的,考虑 A 的 LU 分解 (见“LU 分解 ”),P A = LU ,其中
P 是排列 (permutation) 矩阵 (见“特殊矩阵 (16):排列矩阵 ”),L 和 U 分别为下三角和上三
角矩阵,且 L 的主对角元全都是 1。利用性质九,
(det P )(det A) = (det L)(det U )
对 P A = LU 取转置,得到 A
T
P
T
= U
T
L
T
,同样根据性质九,
(det A
T
)(det P
T
) = (det U
T
)(det L
T
)
注意,三角矩阵 L 和 U 的转置仍为三角矩阵。由性质七,得知 det L = det L
T
= 1,且 det U = det
U
T
。排列矩阵 P 为正交矩阵,满足 P P
T
= I,因此 (det P )(det P
T
) = det I = 1。另外,P 系
由单位矩阵 I 持续交换列而得,可知 det P = ±1,故 det P � det P
T
必同为 1 或-1。综合以上结
果即证得 det A = det A
T
。
另一个证法采用基本矩阵 (elementary matrix) 分解。任一可逆矩阵 A 可分解为 A = E
1
E
2
···E
k
,
其中 E
i
�1 ≤ i ≤ k,是基本矩阵。引用此性质:基本矩阵的转置不改变行列式值,即 det E
T
i
=
det E
i
(见“特殊矩阵 (10):基本矩阵 ”)。因为 A
T
= E
T
k
···E
T
2
E
T
1
,使用性质九,
det A
T
= det(E
T
k
···E
T
2
E
T
1
)
= (det E
T
k
) ···(det E
T
2
)(det E
T
1
)
= (det E
k
) ···(det E
2
)(det E
1
)
= (det E
1
)(det E
2
) ···(det E
k
)
= det(E
1
E
2
···E
k
)
= det A.
我们继续推导高阶行列式的运算方法及一般公式。性质七暗示一个行列式计算方法。对方阵 A
执行基本列运算,仅使用列交换和列取代运算可将 A 化简为上三角矩阵,因为列取代运算不改
变行列式 (性质六),而列交换改变行列式的正负号 (性质四) ,根据性质七,即有下面的公式。
41
3.7 行列式的性质
公式一:轴公式
设 A 为 n 阶方阵,U 为基本列运算 (仅使用列交换和列取代) 化简 A 后得到的上三角矩阵,p
代表所执行的列交换次数,
det A = (−1)
p
det U = (−1)
p
u
11
···u
nn
其中 U 的非零主对角元 u
ii
即为轴元 (pivot)。
重复我们推导二阶行列式的步骤可得三阶行列式,总计分解为 3
3
个行列式之和,但其中仅有
3! = 6 个非零行列式,如下:
a
11
a
12
a
13
a
21
a
22
a
23
a
31
a
32
a
33
= a
11
a
22
a
33
1 0 0
0 1 0
0 0 1
+ a
11
a
23
a
32
1 0 0
0 0 1
0 1 0
+ a
12
a
21
a
33
0 1 0
1 0 0
0 0 1
+ a
12
a
23
a
31
0 1 0
0 0 1
1 0 0
+ a
13
a
21
a
32
0 0 1
1 0 0
0 1 0
+ a
13
a
22
a
31
·
0 0 1
0 1 0
1 0 0
.
每个组合行列式对应一个排列矩阵 P
(α,β,γ)
,(α, β, γ) 代表元 1 出现于元位置 (1, α)�(2, β)�(3, γ),
排列方式计有 6 种:
(1, 2, 3), (1, 3, 2) , (2, 1, 3), (2 , 3, 1), (3, 1, 2), (3, 2, 1)
对单位矩阵
I
执行一序列的列交换即可得到排列矩阵
P
(α,β,γ)
,故 det P
(α,β,γ)
= (−1)
p
,p 表示
从 (1, 2, 3) 至 (α, β, γ) 所执行的置换总数。所以,三阶行列式公式为
a
11
a
12
a
13
a
21
a
22
a
23
a
31
a
32
a
33
= a
11
a
22
a
33
− a
11
a
23
a
32
− a
12
a
21
a
33
+ a
12
a
23
a
31
+ a
13
a
21
a
32
− a
13
a
22
a
31
.
下面是一般 n 阶行列式公式。
公式二:排列公式 (或称莱布尼兹公式)
det A =
X
(α,β,...,ζ)
(a
1α
a
2β
···a
nζ
) · det P
(α,β,...,ζ)
其中 (α, β, . . . , ζ) 表示 (1, 2, . . . , n) 的排列。
上述三阶行列式的任一列皆可作为因数提出,继续代入二阶公式,可得到一个仅含 3 个行列式
的表达形式,以第 1 列为例:
a
11
a
12
a
13
a
21
a
22
a
23
a
31
a
32
a
33
= a
11
(a
22
a
33
− a
23
a
32
) + a
12
(−a
21
a
33
+ a
23
a
31
) + a
13
(a
21
a
32
− a
22
a
31
)
=
a
11
0 0
0 a
22
a
23
0 a
32
a
33
+
0 a
12
0
a
21
0 a
23
a
31
0 a
33
+
0 0 a
13
a
21
a
22
0
a
31
a
32
0
= a
11
c
11
+ a
12
c
12
+ a
13
c
13
.
上式中,我们称 c
ij
为余因子 (cofactor),定义如下:
c
ij
def
= (−1)
i+j
det
˜
A
ij
其中
˜
A
ij
为移除 A 的第 i 列与第 j 行后得到的 (n − 1) × (n − 1) 阶子阵,det
˜
A
ij
称为余子式
(minor)。这个运算公式称为余因子展开或 Laplace 展开公式。
42

3.8 行列式按一行 (列) 展开
公式三:余因子公式 (或称 Laplace 公式)
设 i 为任一列指标,
det A =
n
X
j=1
a
ij
(−1)
i+j
det
˜
A
ij
行列式的性质同时适用于列与行 (column)。如果将 f(A) = f
a b
c d
定义为行向量
a
c
和
b
d
所张的平行四边形面积,只需要将以上讨论的「列」改成「行」,并适当修改推导算式即可。另
外,除了上述三个常见于教科书的行列式运算公式,还有两个鲜为人知的运算法,有兴趣进一步
了解的读者请参阅“Chiò 演算法——另类行列式计算法”和“Dodgson 缩合法——奇特的行列
式运算法”。
3.8 行列式按一行 (列) 展开
有了前面的叙述,我们已经知道,行列式可以按首行或首列展开,这是行列式的递归定义式。事
实上,这可以推广为行列式按任意一行(列)展开。这能容易想到,因为行列式每一项的元素都
来自与不同行不同列。关键在于,按任意行或列展开时,如何确定每一项的正负号。这将是本节
论述的重点。一般来说,将行列式的按某行(列)展开,计算上不见得有多方便,但如果行列式
某一行(列)有较多的 0 元,或者我们能让某行(列)出现较多的 0 元,这就是简化行列式的
好方法。
使用递归定义证明
利用递归定义式2.17和斜对称性,很容易证明行列式可以按任意一行或一列展开。证明过程简写
如下:
证明. 要证行列式可按任意一行(列)展开,我们要证以下两点:
1. 行列式可以按第 j 列展开(第 j 列为任意一列)。
2. 行列式是行列对称的(由此,立即可以得到行列式可以按任意一行展开)。
行列对称的证明已在第3.6节叙述,因此,这里只证第 1 点。要证第 1 点,即是证明展开式的每
一项的正负号与 j 有关。我们可以将行列式的第 j 列往左依次与相邻列交换,则交换第 j −1 次
后,第 j 列会到达第 1 列的位置,而原第 1 列则位于第 2 列,原第 2 列位于第 3 列,以此类
推。由于交换了 j − 1 次,新的行列式与原行列式相差符号 (−1)
j−1
,如下式所示。根据递归定
义式2.17将右式展开,便可证得第一点。
列j
↓
D =
a
11
··· a
1j
··· a
1n
a
21
··· a
2j
··· a
2n
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
a
n1
··· a
nj
··· a
nn
= (−1)
j−1
a
1j
a
11
··· a
1n
a
2j
a
21
··· a
2n
.
.
.
.
.
.
.
.
.
.
.
.
a
nj
a
n1
··· a
nn
= (−1)
j−1
n
X
i=1
(−1)
i+1
a
ij
D
i,j
=
n
X
i=1
(−1)
i+j
a
ij
D
i,j
注意,其中 j 为 {1, 2, ··· , n} 中的某一常数。
43
3.8 行列式按一行 (列) 展开
使用逆序式定义证明
易知,三阶行列式可以归结为二阶行列式的计算,如下:
a
11
a
12
a
13
a
21
a
22
a
23
a
31
a
32
a
33
= a
11
a
22
a
33
+ a
12
a
23
a
31
+ a
13
a
21
a
32
− a
11
a
23
a
32
− a
12
a
21
a
33
− a
13
a
22
a
31
= a
11
(a
22
a
33
− a
23
a
32
) + a
12
(a
23
a
31
− a
21
a
33
) + a
13
(a
21
a
32
− a
22
a
31
)
= a
11
a
22
a
23
a
32
a
33
− a
12
a
21
a
23
a
31
a
33
+ a
13
a
21
a
22
a
31
a
32
对于 n 阶行列式也有类似的性质, 为此我们先引入余子式和代数余子式的概念。
定义3.9 余子式: 在 n 阶矩阵中, 把元素 a
ij
所在的第 i 行和第 j 列划去后, 留下来的元素按原
来的次序构成的一个 n − 1 阶矩阵的行列式叫做元素 a
ij
的余子式, 记作 M
ij
。
M
ij
=
a
11
··· a
1,j−1
a
1,j+1
··· a
1n
.
.
.
.
.
.
.
.
.
.
.
.
a
i−1,1
··· a
i−1,j−1
a
i−1,j+1
··· a
i−1,n
a
i+1,1
··· a
i+1,j−1
a
i+1,j+1
··· a
i+1,n
.
.
.
.
.
.
.
.
.
.
.
.
a
n1
··· a
n,j−1
a
n,j+1
··· a
nn
.
根据行列式的逆序数定义3.7,行列式展开式的每一项的 n 个元素取自不同的行与列,所以对于
某一确定的行中 n 个元素 (譬如 a
i
1
, a
i
2
, ··· , a
in
) 来说,每一项都含有其中的一个且只含有其中
的一个元素。因此,n 级行列式的 n! 项可以分成 n 组,每组有 (n − 1)! 项,即每个元素会出现
有 (n −1)! 次。第一组的项都含有 a
i1
,第二组的项都含有 a
i2
,等等。再分别把第 i 行的元素提
出来,就有
a
11
a
12
··· a
1n
a
21
a
22
··· a
2n
.
.
.
.
.
.
.
.
.
a
n1
a
n2
··· a
nn
= a
i1
A
i1
+ a
i2
A
i2
+ ··· + a
in
A
in
(3.3)
定义3.10 代数余子式: 称 A
ij
为元素 a
ij
的代数余子式,且 A
ij
= (−1)
i+j
M
ij
。
证明. 显然,行列式的递归定义2.17式是3.3式的特殊情况。以下使用行列式的逆序数定义来证明
M
ij
项的符号为 −1
i+j
。
先来证明一个简单的等式,n 级行列式与 n − 1 级行列式有如下关系:
a
11
a
12
··· a
1,n−1
a
1n
a
21
a
22
··· a
2,n−1
a
2n
.
.
.
.
.
.
.
.
.
.
.
.
a
n−1,1
a
n−1,2
··· a
n−1,n−1
a
n−1,n
0 0 ··· 0 1
=
a
11
a
12
··· a
1,n−1
a
21
a
22
··· a
2,n−1
.
.
.
.
.
.
.
.
.
a
n−1,1
a
n−1,2
··· a
n−1,n−1
(I)
(I) 式左端行列式的展开式如下:
X
j
1
j
2
···j
n−1
j
n
(−1)
τ (j
1
j
2
···j
n−1
j
n
)
a
1j
1
a
2j
2
···a
n−1,j
n−1
a
nj
n
其中只有 j
n
= n 的项才可能不为零,而 a
nn
= 1,因此左端为
X
j
1
j
2
···j
n−1
n
(−1)
τ (j
1
j
2
···j
n−1
n)
a
1j
1
a
2j
2
···a
n−1,j
n−1
44

3.8 行列式按一行 (列) 展开
显然 j
1
j
2
···j
n−1
是 1, 2, ··· , n − 1 的排列,且
τ (j
1
j
2
···j
n−1
n) = τ (j
1
j
2
···j
n−1
)
由此可知,左式等右式,(I) 式得证。
根据3.3式,我们要证明 A
ij
= (−1)
i+j
M
ij
,而 A
ij
的值与 a
ij
的取值无关,因此,令:
a
i1
= ··· = a
i,j−1
= a
i,j+1
= ··· = a
in
= 0, a
ij
= 1
可得
A
ij
=
a
11
··· a
1,j−1
a
1j
a
1,j+1
··· a
1n
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
a
i−1,1
··· a
i−1,j−1
a
i−1,j
a
i−1,j+1
··· a
i−1,n
0 ··· 0 1 0 ··· 0
a
i+1,1
··· a
i+1,j−1
a
i+1,j
a
i+1,j+1
··· a
i+1,n
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
a
n1
··· a
n,j−1
a
nj
a
n,j+1
··· a
nn
= (−1)
n−i
a
11
··· a
1,j−1
a
1j
a
1,j+1
··· a
1n
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
a
i−1,1
··· a
i−1,j−1
a
i−1,j
a
i−1,j+1
··· a
i−1,n
a
i+1,1
··· a
i+1,j−1
a
i+1,j
a
i+1,j+1
··· a
i+1,n
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
a
n1
··· a
n,j−1
a
nj
a
n,j+1
··· a
nn
0 ··· 0 1 0 ··· 0
= (−1)
(n−i)+(n−j)
a
11
··· a
1,j−1
a
1,j+1
··· a
1n
a
1j
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
a
i−1,1
··· a
i−1,j−1
a
i−1,j+1
··· a
i−1,n
a
i−1,j
a
i+1,1
··· a
i+1,j−1
a
i+1,j+1
··· a
i+1,n
a
i+1,j
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
a
n1
··· a
n,j−1
a
n,j+1
··· a
nn
a
nj
0 ··· 0 0 ··· 0 1
= (−1)
2
n
−
(
i
+
j
)
M
ij
= (−1)
i
+
j
M
ij
这里, 第一步是依次地把第 i 行与它下边的一行对换,直到把它换到第 n 行为止,这样一共换了
n − i 次,因之行列式差一个符号 (−1)
n−i
;第二步是同样地把第 j 列换到第 n 列。最后,再利
用 (I) 式与显然的关系 (−1)
2n−(i+j)
= (−1)
i+j
。
根据3.3式和 A
ij
= (−1)
i+j
M
ij
,可得到行列式按一行或一列的展开式,展开式由该行(列)的
代数余子式组成,这是行列式递归定义的推广。容易看出,当固定了某一行(或某一列),那么
代数余子式的符号是依次交错的。例如:按第一列展开,第一个 A 为正,第二个为负,第三个
为正等等。
定义3.11 行列式的行 (列) 展开式: n 阶行列式 D 定义为
a
11
a
12
··· a
1n
a
21
a
22
··· a
2n
.
.
.
.
.
.
.
.
.
.
.
.
a
21
a
22
··· a
2n
=
n
X
i=1
(−1)
i+j
a
ij
D
i,j
其中每一个 D
i,j
, 1 ≤ i ≤ n,都是低一阶的子行列式,它们把原来 n 阶行列式内的第 i 行和第
j 列删去。
45

3.9 拉普拉斯定理
定理 3.4
对于任意 n 阶行列式 D,A
ij
表示 D 的元素 a
ij
的代数余子式,以下公式成立
n
X
j=1
a
kj
A
ij
= a
k1
A
i1
+ a
k2
A
i2
+ ··· + a
kn
A
in
=
D
k = i
0
k 6= i
n
X
i=1
a
il
A
ij
= a
1l
A
1j
+ a
2l
A
2j
+ ··· + a
nl
A
nj
=
D
l = j
0
l 6= j
即某行(列)的元素与其它行(列)相应元素的代数余子式的乘积之和为 0。
由行列式的交错性,容易证明上述定理,因此,在此省略证明过程。
3.9 拉普拉斯定理
定义3.12 k 级子式: 将 n 阶行列式 D 的某 k 行与某 k 列按原次序排列形成的新行列式 M 被
称为 D 的 k 级子式。
定义3.13 余子式: 将 n 阶行列式 D 的某 k 行与某 k 列去掉后,余下的元素按原次序组成的
n − k 级行列式 M
′
称为 k 级子式 M 的余子式。
定义3.14 代数余子式: 设 n 阶行列式 D 的 k 级子式 M 在 D 中所在的行、列指标分别是
i
1
, i
2
, ··· , i
k
和 j
1
, j
2
, ··· , j
k
。则 M 的余子式 M
′
前面加上符号 (−1)
(i
1
+i
2
+···+i
k
)+(j
1
+j
2
+···+j
k
)
后称做 M 的代数余子式。
例子:在如下四阶行列式中,选定第一、三行,第二、四列得到一个二阶子式 M
1 2 1 4
0 −1 2 1
0 0 2 1
0 0 1 3
M =
2 4
0 1
M 的余子式为
M
′
=
0 2
0 1
定理 3.5. 拉普拉斯定理
在 n 阶行列式 D 中任取 k 行 (1 ≤ k ≤ n),由这 k 行元素组成的所有 k 阶子式 M 与它
们的代数余子式 A 的乘积之和等于行列式 D 的值,即:
D = M
1
A
1
+ M
2
A
2
+ ··· + M
t
A
t
其中,t = C
k
n
=
n!
k!(n−k)!
,因为 M 中有 k! 项,A 有 (n − k)! 项,D 应有 n! 项。
证明. 拉普拉斯定理的证明可归结为证明如下两点:
1. 任意一个子式 M 与它的代数余子式 A 的乘积的每一项都是行列式 D 展开式中的一项
2. 等式两边项数相等
1
先证第 1 点,即证明以下引理:
引理 3.1
行列式 D 的任一个子式 M 与它的代数余子式 A 的乘积中的每一项都是行列式 D 的展
开式中的一项,而且符号也一致。
首先讨论 M 位于行列式 D 的左上方的情形:
46
3.9 拉普拉斯定理
D =
a
11
a
12
··· a
1k
a
1,k+1
··· a
1n
.
.
. M
.
.
.
.
.
.
.
.
.
a
k
1
a
k
2
··· a
kk
a
k,k
+1
··· a
kn
a
k+1,1
a
k+1,2
··· a
k+1,k
a
k+1,k+1
··· a
k+1,n
.
.
.
.
.
.
.
.
.
.
.
. M
′
.
.
.
a
n1
a
n2
··· a
nk
a
n,k+1
··· a
nn
此时 M 的代数余子式 A 为
A = (−1)
(1+2+···+k)+(1+2+··· +k)
M
′
= M
′
M 的每一项都可写作
a
1α
1
a
2α
2
···a
ka
k
其中 α
1
, α
2
, ··· , α
k
是 1, 2, ··· , k 的一个排列,所以这一项前面的符号为 (−1)
τ (a
1
α
2
···α
k
)
。
M
′
中每一项都可写作
a
k+1,β
k+1
a
k+2,β
k+2
···a
nβ
n
其中 β
k+1
, β
k+2
, ··· , β
n
是 k + 1, k + 2, ··· , n 的一个排列, 这一项 在 M
′
中前面所带的符号是
(−1)
τ ((β
k+1
−k)(β
k+2
−k)···(β
n
−k))
M
与
M
′
乘积的每一项可写为
a
1a
1
a
2α
2
···a
ka
k
a
k+1,β
k+1
···a
nβ
n
前面的符号是
(−1)
τ (a
1
α
2
···α
k
)+τ ((β
k+1
−k)(β
k+2
−k)···(β
n
−k))
因为每个 β 比每个 α 都大, 所以上述符号等于
(−1)
τ (α
1
α
2
···α
k
β
k+1
···β
n
)
因此这个乘积是行列式 D 中的一项而且符号相同。
下面来证明一般情形。设子式 M 位于 D 的第 i
1
, i
2
, ··· , i
k
行, 第 j
1
, j
2
, ··· , j
k
列, 这里
i
1
< i
2
< ··· < i
k
, j
1
< j
2
< ··· < j
k
变动 D 中行列的次序使 M 位于 D 的左上角。为此,先把第 i
1
行依次与第 i
1
−1, i
1
−2, ··· , 2, 1
行对换。这样经过了 i
1
−1 次对换而将第 i
1
行换到第一行。再将 i
2
行依次与第 i
2
−1, i
2
−2, ···2
行对换而换到第二行,一共经过了 i
2
− 2 次对换。如此继续进行,一共经过了
(i
1
− 1) + (i
2
− 2) + ··· + (i
k
− k)
= (i
1
+ i
2
+ ··· + i
k
) − (1 + 2 + ··· + k)
次行对换而把第 i
1
, i
2
, ··· , i
k
行依次换到第 1, 2, ··· , k 行。利用类似的列变换,可以将 M 的列
换到第 1, 2, ··· , k 列。一共作了
(j
1
− 1) + (j
2
− 2) + ··· + (j
k
− k)
= (j
1
+ j
2
+ ··· + j
k
) − (1 + 2 + ··· + k)
次列变换。
47

3.9 拉普拉斯定理
我们用 D
1
表示这样变换后所得的新行列式。那么
D
1
= (−1)
(i
1
+i
2
+···+i
k
)−(1+2+···+k)+(j
1
+j
2
+···+j
k
)−(1+2+···+k)
D
= (−1)
i
1
+i
2
+···+i
k
+j
1
+j
2
+···+j
k
D
即
D = (−1)
i
1
+i
2
+···+i
k
+j
1
+j
2
+···+j
k
D
1
由此看出, D
1
和 D 的展开式中出现的项是一样的, 只是每一项都差符号 (−1)
i
1
+···+i
k
+j
1
+···+j
k
。
现在 M 位于 D
1
的左上角, 所以 M · M
′
中每一项都是 D
1
中的一项而且符号一致。但是
M · A = (−1)
i
1
+···+i
k
+j
1
+···+j
k
M · M
′
= (−1)
i
1
+···+i
k
+j
1
+···+j
k
D
1
所以 MA 中每一项都与 D 中一项相等而且符号一致。
2 再证第 2 点。显然等式左边共有 n! 项,为了计算右边的项数,首先来求出根据 k 级子式的
数量 t
t = C
k
n
=
n!
k!(n − k)!
因为 M
i
中共有 k! 项,A
i
中共有 (n − k)! 项。所以右边共有
t · k! · (n − k)! = n!
项。根据引理, M
i
A
i
中每一项都是 D 中一项而且符号相同,而且 M
i
A
i
和 M
j
A
j
(i 6= j) 无公共
项,又因为等式两边项数相等,因此等式成立,拉普拉斯定理得证。
可以看出,根据拉普拉斯定理,将行列式按零元较多的行或列展开,能够大大简化计算。如果行
列式中的元素零不多,可以按照一些规则创造一些零,这需要利用行列式的性质。
3.9.1 范德蒙行列式
范德蒙行列式:
D
n
=
1 1 ··· 1
x
1
x
2
··· x
n
x
2
1
x
2
2
··· x
2
n
.
.
.
.
.
.
.
.
.
.
.
.
x
n−1
1
x
n−1
2
··· x
n−1
n
=
Y
1≤j<i≤n
(x
i
− x
j
).
证明. 用数学归纳法.
D
2
=
1 1
x
1
x
2
= x
2
− x
1
, 所以 n = 2 时结论成立.
现假设 n − 1 时结论成立, 下证 n 时结论也成立: 因为
48

3.9 拉普拉斯定理
D
n
r
n
− x
1
r
n−1
r
n−1
− x
1
r
n−2
========
.
.
.
r
2
− x
1
r
1
1 1 ··· 1
0 x
2
− x
1
··· x
n
− x
1
0 x
2
(x
2
− x
1
) ··· x
n
(x
n
− x
1
)
.
.
.
.
.
.
.
.
.
.
.
.
0 x
n−2
2
(x
2
− x
1
) ··· x
n−2
n
(x
n
− x
1
)
= (x
2
− x
1
)(x
3
− x
1
) ···(x
n
− x
1
)
1 1 ··· 1
x
2
x
3
··· x
n
x
2
2
x
2
3
··· x
2
n
.
.
.
.
.
.
.
.
.
.
.
.
x
n−1
2
x
n−1···
3
··· x
n−1
n
= (x
2
− x
1
)(x
3
− x
1
) ···(x
n
− x
1
)
Q
2≤j<i≤n
(x
i
− x
j
) =
Q
1≤j<i≤n
(x
i
− x
j
).
所以命题成立.
49
3.9 拉普拉斯定理
50
第四章 向量空间
笛卡儿在 1637 年发表的著作中用两个坐标来描述平面。向量空间是平面的一种推
广。
利用行列式可以判断数域 P 上 n 个方程的元线性方程组有没有唯一解,但是无法分辨无解和有
无穷多个解的情形,也不能用于判断方程个数与未知量个数不相等的线性方程组有无解、有多少
解。因此需要另辟途径来研究直接从线性方程组的系数和常数项判断它有没有解,有多少解的
问题,并且要研究线性方程组有无穷多个解时其解集的结构。
4.1 n 维向量
定义4.1 n 维向量: 数域 P 上一个 n 维向量就是由数域 P 中 n 个数 a
1
, a
2
, ··· , a
n
组成的有序
数组,记为
α = (α
1
, α
2
, ··· , α
n
)
其中 α
i
称为 α 第 i 个分量。向量的印刷体一般用粗体小写字母表示,如 α, β, γ。向量的手写
体一般用带就箭头的小写字母表示,如 ⃗α,
⃗
β, ⃗γ。
◦ 当 F 取 R 时,称 α 为实向量。
◦ 当 F 取 C 时,称 α 为复向量。
引入坐标系后,n 维度向量 (a
1
, a
2
, ··· , a
n
) 在几何中可以被等价定义为 n 维空间的一个点 A,
或者起点在原点 O,指向终点 A 的箭头。此时,向量也可记为
−→
OA。当 n > 3 的时候,向量没
有直观的几何意义。
定义4.2 相等: 如果 n 维向量 α = (a
1
, a
2
, ··· , a
n
), β = (b
1
, b
2
, ··· , b
n
) 的对应分量都相等,即
a
i
= b
i
(i = 1, 2, ··· , n),就称这两个向量是相等的,记作 α = β。
我们把线性方程组的增广矩阵经过初等行变换化成阶梯形矩阵后,就能判断原线性方程组有无
解,有多少解。而初等行变换包含“倍乘”和“倍加”两种运算。受此启发,我们可以在数域 P
上的所有 n 元有序数组组成的集合 P
n
中定义向量加法和数量乘法运算。
定义4.3 向量加法: 向量 γ = (a
1
+ b
1
, a
2
+ b
2
, ··· , a
n
+ b
n
) 称为向量 α = (a
1
, a
2
, ··· , a
n
), β =
(b
1
, b
2
, ··· , b
n
) 的和,记为 γ = α + β。
向量的加法满足以下四条运算律:
1. 交换律:α + β = β + α
2. 结合律:α + (β + γ) = (α + β) + γ
3. 存在单位元:α + 0 = α
4. 存在逆元:α + (−α) = 0
定义4.4 数量乘积: 设 k 为数域 P 中的数,向量 (ka
1
, ka
2
, ··· , ka
n
) 称为向量 α = (a
1
, a
2
, ··· , a
n
)
与数 k 的数量乘积,记为 kα。
51
4.2 线性相关
1. k(α + β) = kα + kβ
2. (k + l)α = kα + lα
3. k(lα) = klα
4. 1α = α
⋇ 0α = 0
⋇ −1(α) = −α
⋇ k0 = 0
⋇ 若 k 6= 0, α 6= 0,kα 6= 0
定义4.5 零向量: 分量全为零的向量 (0�0� ···�0),记为 0。
定义4.6 负向量: 向量 (−a
1
� −a
2
� ···� − a
n
) 称为向量 α = (a
1
�a
2
� ···�a
n
) 的负向量,记为 −α。
定义4.7 向量减法: 利用负向量定义和向量加法定义向量减法:α − β = α + (−β)。
定义4.8 n 维向量空间: 以数域 P 中的数作为分量的 n 维向量的全体,同时考虑到定义在它们
上面的加法和数量乘法,称为数域 P 上的 n 维向量空间。
以上已把数域 P 上全体 n 维向量的集合组成一个有加法和数量乘法的代数结构,即数域 P 上
n 维向量空间。之后进一步讨论向量之间的关系和性质,并用这些性质描述和解决线性方程组中
的一些问题。
向量通常是写成一行(如左式),有时也可以写成一列(如右式):
α = (a
1
, a
2
, ··· , a
n
) α =
a
1
a
2
.
.
.
a
n
为了区别,前者称为行向量,后者称为列向量。它们的区别只是写法上的不同。
4.2 线性相关
定义4.9 成比例: α = kβ,就是数乘关系。
定义4.10 线性组合: 给定向量组 A : α
1
, α
2
, ··· , α
n
和向量 β,若存在一组实数 k
1
, k
2
, ··· , k
n
,
使得:
β = k
1
α
1
+ k
2
α
2
+ ··· + k
n
α
n
则称向量 β 是向量组 α
1
, α
2
, ··· , α
n
的一个线性组合;也说向量 β 可以由向量组 α
1
, α
2
, ··· , α
n
线性表出。
由线性组合的定义可知,零向量是任意向量组的线性组合,只要系数全为 0 即可。任一个 n 维
向量 α = (a
1
, a
2
, ··· , a
n
) 都是单位向量组的一个线性组合。容易推断出,向量组的线性表出具
有传递性。即:
1. 向量组 α
1
, α
2
, ··· , α
t
可以经向量组 β
1
, β
2
, ··· , β
s
线性表出。
2. 向量组 β
1
, β
2
, ··· , β
s
可以经向量组 γ
1
, γ
2
, ··· , γ
p
线性表出。
3. 由 1、2 可得,向量组 α
1
, α
2
, ··· , α
t
可以经向量组 γ
1
, γ
2
, ··· , γ
p
线性表出。
定义4.11 向量组的等价: 如果向量组 α
1
, α
2
, ··· , α
t
中每一个向量 α
i
(i = 1, 2, ··· , t) 都可以经
向量组 β
1
, β
2
, ··· , β
s
线性表出,那么向量组 α
1
, α
2
, ··· , α
t
就称为可以经向量组 β
1
, β
2
, ··· , β
s
线性表出。如果两个向量组互相可以线性表出,它们就称为等价。
52
4.2 线性相关
根据向量组等价的定义,不难验证其符合等价的三个性质:反身性、对称性和传递性。
定义4.12 线性相关 1: 如果向量组 α
1
, α
2
, ··· , α
s
(s ≥ 2) 中有一个向量是可以由其余的向量
线性表出,那么向量组 α
1
, α
2
, ··· , α
s
线性相关。(直接由线性组合(线性表出)的定义得到)
由定义可知,任意一个包含零向量的向量组一定是线性相关的。在二维欧式空间,若向量组 α
1
, α
2
线性相关,表示它们成比例,即 α
1
= kα
2
或者 α
2
= kα
1
(这两个式子不一定能同时成立),这
意味着向量 α
1
, α
2
共线。在三维欧式空间,三个向量 α
1
, α
2
, α
3
线性相关意味着它们共面。
线性相关还有另一个定义方式。
定义4.13 线性相关 2: 向量组 α
1
, α
2
, ··· , α
s
(s ≥ 1) 称为线性相关的,如果有数域 P 中不全
为零的数 k
1
, k
2
, ··· , k
s
,使 k
1
α
1
+ k
2
α
2
+ ··· + k
s
α
s
= 0。
定义4.14 线性无关: 对于向量组 α
1
, α
2
, ··· , α
s
(s ≥ 1),没有一组不全为零的数 k
1
, k
2
, ··· , k
s
,
使 k
1
α
1
+ k
2
α
2
+ ··· + k
s
α
s
= 0,就称它是线性无关的;或者说,一向量组 α
1
, α
2
, ··· , α
s
称
为线性无关,如果由 k
1
α
1
+ k
2
α
2
+ ··· + k
s
α
s
= 0 可以推出 k
1
= k
2
= ··· = k
s
= 0。
稍加分析,不难发现,线性相关的两个定义在 s ≥ 2 时是一致的,而第二个定义额外说明了只含
一个向量 α 的向量组的情况,若 α 6= 0,则该向量组线性无关,若 α = 0,则该向量组线性相
关。注意的是,一个向量组线性相关并不意味着所有向量都能被剩余的向量线性表出。只要其中
有一个向量能被其余向量线性表出,那这个向量组即是线性相关的。
我们已经知道,对于如下线性方程组:
a
11
x
1
+ a
12
x
2
+ ··· + a
1s
x
s
= b
1
a
21
x
1
+ a
22
x
2
+ ··· + a
2s
x
s
= b
2
.
.
.
a
n1
x
1
+ a
n2
x
2
+ ··· + a
ns
x
s
= b
n
根据向量加法和数乘的定义,将未知量的系数按列组合,上述线性方程组可以表示为一个线性组
合:x
1
α
1
+ x
2
α
2
+ ··· + x
s
α
s
= b。将之与线性相关的两个定义作对比,可以发现,线性相关
的第一个定义对应非齐次线性方程组,而第二个定义对应齐次线性方程组。由此可知,具体判断
一个(列)向量组是否线性相关的问题可以归结为解线性方程组的问题。
线性代数的教材一般会给出以上两个线性相关的定义。我相信不少人会感觉奇怪,这两个定义
几乎是一致的,就像一句话重复了两次。其实,第 1 个线性相关的定义是最符合数学直觉的,但
若根据第 1 个定义来判断一个含有 n(n ≥ 2) 个向量的向量组是否线性相关,则最坏的情况下需
要解 n 个含有 n − 1 个未知量的线性方程组。如果使用第 2 个线性相关的定义,则只需要解 1
个含有 n 个未知量的齐次线性方程组即可。
一般地,要判断一个(列)向量组 α
i
= (a
1i
, a
2i
, ··· , a
ni
), i = 1, 2, ··· , s 是否线性相关,就是看
方程 x
1
α
1
+ x
2
α
2
+ ···+ x
s
α
s
= 0 有无非零解。也就是说,列向量组 α
1
, α
2
, ··· , α
s
线性无关
的充分必要条件是对应的齐次线性方程组只有零解。
另一方面,将线性方程组的系数按行组合,可得到一个行向量组 β
1
, β
2
, ··· , β
n
,其中
β
i
= (a
i1
, a
i2
, ··· , a
is
, b
i
), i = 1, 2, ··· , n
如果 β
1
, β
2
, ··· , β
n
行向量组线性相关,那说明某个方程可通过初等变换消去,即该方程是无效
的。基于以上定义和论述,容易推导出以下命题。
命题 4.1 如果一个向量组有部分组是线性相关的,那么这个向量组一定线性相关。
证明. 设 α
1
, α
2
, ··· , α
r
线性相关,且是 α
1
, α
2
, ··· , α
s
的部分组。由定义 2 可知,存在不全为
0 的数 k
1
, k
2
, ··· , k
r
使下式成立:
k
1
α
1
+ k
2
α
2
+ ··· + k
r
α
r
= 0
因此,显然下式也成立 (k
r+1
, ··· , k
s
全为 0):
53

4.2 线性相关
k
1
α
1
+ k
2
α
2
+ ··· + k
r
α
r
+ 0α
r+1
+ ··· + 0α
s
= 0
由第二个定义知,α
1
, α
2
, ··· , α
s
线性相关。
命题 4.2 如果一个向量组线性无关,那么它的任何一个非空的部分组也线性无关。(命题 1 的逆
否)
命题 4.3 由 n 维单位向量组成的向量组线性无关。
证明. 由 n 维单位向量和线性无关的定义:
k
1
ε
1
+ k
2
ε
2
+ ··· + k
n
ε
n
=k
1
(1, 0, ··· , 0) + k
2
(0, 1, ··· , 0) + ··· + k
n
(0, 0, ··· , 1)
= (k
1
, k
2
, ··· , k
n
)
=(0, 0, ··· , 0)
可以推出 k
1
= k
2
= ··· = k
n
= 0。这就是说, ε
1
, ε
2
, ··· , ε
n
线性无关。
命题 4.4 如果向量组 α
i
= (a
i1
, a
i2
, ··· , a
in
) , i = 1, 2, ··· , s 线性无关,那么在每一个向量上添
m 个分量所得到的 n + m 维的向量组 β
i
= (a
i1
, a
i2
, ··· , a
in
, a
i,n+1
, ··· , a
i,n+m
) 也线性无关。
证明. 因为向量组 α
i
= (a
i1
, a
i2
, ··· , a
in
) , i = 1, 2, ··· , s 线性无关,因此它对应的齐次线性方程
组 (A) 只有零解。而因为向量组 β
i
的齐次线性方程组 (B) 就是在 (A) 的基础上添加了 m 个方
程。显然,(B) 的解必然是 (A) 的解,而 (A) 的解包含 (B) 的解。因为 (A) 只有零解,而 (B)
也必有零解,因此 (B) 有解,且只有零解。
由定理2.2(齐次线性方程组非零解存在定理),可得到向量组的一个基本性质。定理4.1非常重
要,因为这一章余下的命题、推断或定理几乎都由定理4.1直接或间接证得。
定理 4.1
设 α
1
, α
2
, ··· , α
r
与 β
1
, β
2
, ··· , β
s
是两个向量组。如果满足如下两个条件,那么向量组
α
1
, α
2
, ··· , α
r
必线性相关。
1. 向量组 α
1
, α
2
, ··· , α
r
可以经 β
1
, β
2
, ··· , β
s
线性表出
2. r > s
证明. 由条件 1 可得:
α
i
=
s
X
j=1
t
ji
β
j
i = 1, 2, ··· , r
为了证明 α
1
, α
2
, ··· , α
r
线性相关,只要证可以找到不全为 0 的 x
1
, ··· , x
r
,使得下式成立
x
1
α
1
+ x
2
α
2
+ ··· + x
r
α
r
= 0
x
1
α
1
+ x
2
α
2
+ ··· + x
r
α
r
=
r
X
i=1
x
i
s
X
j=1
t
ji
β
j
=
r
X
i=1
s
X
j=1
t
ji
x
i
β
j
=
r
X
i=1
(
s
X
j=1
t
ji
x
i
)
β
j
∵
s
X
j=1
(
r
X
i=1
t
ji
x
i
)β
j
= (
r
X
i=1
t
ji
x
i
)β
1
+ (
r
X
i=1
t
ji
x
i
)β
2
+ ··· + (
r
X
i=1
t
ji
x
i
)β
s
如果能找到不全为 0 的 x
1
, ··· , x
r
使得 β
1
, β
2
, ··· , β
s
的系数全为 0,那就证明了 α
1
, α
2
, ··· , α
r
线性相关。
54

4.3 极大线性无关组
由上式可得到一个齐次线性方程组:
t
11
x
1
+ t
12
x
2
+ ··· + t
1r
x
r
= 0
t
21
x
1
+ t
22
x
2
+ ··· + t
2r
x
r
= 0
.
.
.
t
s1
x
1
+ t
s2
x
2
+ ··· + t
sr
x
r
= 0
因为条件 2:r > s,未知量的个数大于方程的个数,由定理2.2,方程组有非 0 解。
推断 4.1-1 如果向量组 α
1
, α
2
, ··· , α
r
可以经向量组 β
1
, β
2
, ··· , β
s
线性表出,且 α
1
, α
2
, ··· , α
r
线性无关,那么 r ≤ s。
证明. 证明过程与定理4.1相似。因为 α
1
, α
2
, ··· , α
r
线性无关,齐次线性方程组只有零解。又
因为其中任意一个方程都不能通过初等变换消去,所以未知量的个数不能多于方程的个数,即
r ≤ s。
推断 4.1-2 任意 n + 1 个 n 维向量必线性相关。
证明. 每个 n 维向量都可以被 n 维单位向量线性表出,且 n + 1 > n,由定理4.1可知必线性相
关。
推断 4.1-3 两个线性无关的等价的向量组,必含有相同个数的向量。
证明. 应用两次推论4.1-1可证。
4.3 极大线性无关组
定义4.15 极大线性无关组: 一向量组的一个部分组称为一个极大线性无关组,如果这个部分组
是线性无关的,并且往这个向量组中任意添一个向量(如果还有的话),所得到的新部分组都线
性相关。
显然,一个线性无关向量组的极大线性无关组就是这个向量组本身。由命题4.5和定理4.3可以看
出,极大线性无关组就是相应向量组的最小等价向量组。那么,研究一个向量组的性质就可以转
为研究它的最小等价向量组的性质。
命题 4.5 任意一个极大线性无关组都与向量组本身等价。(极大线性无关组的基本性质)
证明. %
1. 向量组显然能线性表出极大线性无关组。
2. 设 α
1
, α
2
, ··· , α
r
是 α
1
, α
2
, ··· , α
s
的极大线性无关组。显然,极大线性无关组能线性表
出自身任一向量。关键是证明 α
1
, α
2
, ··· , α
r
能线性表出 α
r+1
, α
r+2
, ··· , α
s
。
现在从 α
r+1
, α
r+2
, ··· , α
s
任选一个向量 α
w
加入极大线性无关组。由极大线性无关组的
定义可知,α
1
, α
2
, ··· , α
r
, α
w
线性相关。
如果能够证明 α
w
能由 α
1
, α
2
, ··· , α
r
线性表出,就证明了命题。
现有如下式成立
k
1
α
1
+ k
2
α
2
+ ··· + k
r
α
r
+ k
w
α
w
= 0
假设 k
w
= 0,那么 k
1
, k
2
, ··· , k
r
至少一个不为 0,上式变为
k
1
α
1
+ k
2
α
2
+ ··· + k
r
α
r
= 0
又因为 α
1
, α
2
, ··· , α
r
线性无关,所以 k
1
, k
2
, ··· , k
r
全部为 0。故此产生矛盾,可知 k
w
必不为 0。因此有
α
w
= −
k
1
k
w
α
1
−
k
2
k
w
α
2
− ··· −
k
r
k
w
α
r
由此可知 α
r+1
, α
r+2
, ··· , α
s
能被极大线性无关组线性表出。
基于上面命题的证明过程,再细加推导,可以得出如下定理。
55

4.3 极大线性无关组
定理 4.2. 线性表示的唯一性
向量组 α
1
, α
2
, ··· , α
r
线性无关,而向量组 α
1
, α
2
, ··· , α
r
, β 线性相关。则向量 β 可以
由向量组 α
1
, α
2
, ··· , α
r
线性表示,且表示法唯一。
以上内容亦可叙述如下:
假设向量向量 β 可以由向量组 α
1
, α
2
, ··· , α
r
线性表出,则表示法唯一的充分必要条件
是向量组 α
1
, α
2
, ··· , α
r
线性无关。
证明. 以上两种叙述类似,但第一种叙述的前提条件稍弱一些,需要先由以下两个条件推导出向
量 β 可以由向量组 α
1
, α
2
, ··· , α
r
线性表出。
1. 向量组 α
1
, α
2
, ··· , α
r
线性无关
2. 而向量组 α
1
, α
2
, ··· , α
r
, β 线性相关
具体推导过程可参考命题4.5的证明过程。以下证明以第二种叙述为基础。
先证充分性。要证明表示法唯一,亦即证明使得以下公式成立的系数 (k
1
, k
2
, ··· , k
r
) 是唯一的
k
1
α
1
+ k
2
α
2
+ ··· + k
r
α
r
= β (I)
由此可以想到,我们可以利用线性方程组的唯一解条件。因为向量组 α
1
, α
2
, ··· , α
r
线性无关,
根据推论4.1-2和定理5.1,向量 α
i
的维度 n 大于或等于 r,且方程组 (I) 必有 r 个有效的方程,
其余 n − r 个方程可由这 r 个有效的方程进行初等变换得到,因此,其余 n − r 个方程和 r 个
有效方程同解。根据线性方程组解的情况及其判别准则 (2.2节),r 个方程、r 个变量,此时方程
组 (I) 必有唯一解 (k
1
, k
2
, ··· , k
r
)。
再证明必要性。因为表示法唯一,即线性方程组 (I) 有唯一解。根据2.2节的内容,(I) 必有且
仅有 r 个有效的方程。也就是说,(I) 的系数矩阵的行秩为 r,因为矩阵的行秩等于列秩,而
α
1
, α
2
, ··· , α
r
是系数矩阵的 r 个列向量,因此 α
1
, α
2
, ··· , α
r
必然线性无关。
虽然向量组的极大线性无关组不是唯一的,但有如下命题成立:
命题 4.6 向量组的所有极大线性无关组等价。
证明. 每一个极大线性无关组都与向量组本身等价,由等价的传递性可知:一向量组的任意两个
极大线性无关组都是等价的。
来看一个例子:有向量组 α
1
= (1, 0, 0), α
2
= (0, 1, 0), α
3
= (1, 1, 0),在这里{α
1
, α
2
}线
性无关,而 α
3
= α
1
+ α
2
,所以{α
1
, α
2
}是一个极大线性无关组。另一方面 {α
1
, α
3
},
{α
2
, α
3
} 也都是向量组{α
1
, α
2
, α
3
}的极大线性无关组。
虽然,极大线性无关组不唯一,但我们发现上述例子中,极大线性无关组的向量个数是一
样的,那这是不是一个普遍的性质呢?
定理 4.3
一向量组的极大线性无关组都含有相同个数的向量。
证明. 因为极大线性无关组与向量组本身等价,再由等价的传递性可知,同一向量组的所有极大
线性无关组等价。由推论4.1-3可知,它们的向量个数相等。
定理4.3表明,极大线性无关组所含向量的个数与极大线性无关组的选择无关,它直接反映
了向量组本身的性质。由此定义向量组的秩。
定义4.16 向量组的秩: 向量组的极大线性无关组所含向量的个数称为这个向量组的秩。
命题 4.7 一向量组线性无关的充要条件是它的秩与它所含向量的个数相同。
56

4.3 极大线性无关组
含有非零向量的向量组一定有极大线性无关组
1
,且任一个线性无关的部分向量都能扩充成一极
大线性无关组。全部由零向量组成的向量组没有极大线性无关组,规定这样的向量组的秩为零。
命题 4.8 等价的向量组必有相同的秩。
证明. 由推论4.1-3知:等价的线性无关向量组含有相同个数的向量。
每一向量组都与它的极大线性无关组等价。由等价的传递性可知,任意两个等价向量组的极大
线性无关组也等价。应用推论4.1-3,得证。
在引入了秩的概念后,定理4.1可以等价
2
叙述为以下命题。
命题 4.9 如果向量组 (A) 可由向量组 (B) 线性表出,那么 (A) 的秩不超过 (B) 的秩。
证明. 假设向量组 (A) 和向量组 (B) 的极大线性无关组分别为 (α) 和 (β)。因为向量组 (A) 可
由向量组 (B) 线性表出,由于极大线性无关组 和向量组本身等价,因此,向量组 (α) 可由 (β)
线性表出。设 (α) 和 (β) 的向量个数分别为 a 和 b,也就是 ( A) 和 (B) 的秩分别为 a 和 b。根
据定理4.1,若 a > b,则向量组 (α) 线性相关。这与 ( α) 是极大线性无关组矛盾。因此,a ≤ b,
即 (A) 的秩不超过 (B) 的秩。
实际上,在引入线性空间和维度的概念后,定理4.1和命题4.9会有一个更直观的理解:向量组不
能张成维度高于其秩的线性空间。
根据命题4.9或者命题4.8,可以推导出以下命题。
命题 4.10 初等变换不会改变向量组的秩。
证明. 初等行变换有三种:
1. 将第 i 行(列)加到第 j 行(列)
2. 将第 i 行(列)乘以一个非零实数 k
3. 交换第 i 行(列)和第 j 行(列)的位置
现在我们基于定义4.16和命题4.9来证明本命题。实际上,要证明初等变换不会改变向量组的秩,
只需证明一次初等变换不会改变向量组的秩即可。假设现有向量组 (A) 如下:
α
1
, α
2
, ··· , α
i
, ··· , α
j
, ··· , α
n
将第 i 个向量加到第 j 个向量个向量,得到新的向量组 (A
1
) 如下:
α
1
, α
2
, ··· , α
i
, ··· , β
j
, ··· , α
n
其中,β
j
= α
i
+ α
j
。显然,向量组 (A) 和 (A
1
) 具有 n − 1 个相同的向量,它们在这 n − 1 个
向量上可以相互线性表出。向量组 (A) 和 (A
1
) 只有第 j 个向量是不同的,但它们也能相互线性
表出第 j 个向量,如下:
β
j
= 0α
1
+ 0α
2
+ ··· + α
i
+ ··· + α
j
+ ··· + 0α
n
α
j
= 0α
1
+ 0α
2
+ ··· + α
i
+ ··· + (−1)β
j
+ ··· + 0α
n
因此,此时向量组 (A) 和 (A
1
) 是等价的,它们具有相同的秩。
将向量组 (A) 的第 i 个向量乘以非零实数 k,得到新向量组 (A
2
):
α
1
, α
2
, ··· , β
i
, ··· , α
j
, ··· , α
n
其中,β
i
= kα
i
。不难证明,向量组 (A) 和 (A
2
) 也是等价的,因此它们具有相同的秩。
1
若向量组只含有一个且非零的向量,其秩为 1。
2
在这里,等价的意思是:若定理4.1成立,则可推导出命题4.9;反之,若命题4.9成立,亦可推导出定理4.1。
57

4.3 极大线性无关组
根据定义4.16,向量组的秩和向量的排列次序是没有关系的,而交换第 i 个向量和第 j 个向量的
位置并不会改变向量组,因此交换前后,秩不变。
现在把上面的概念与方程组的解的关系进行联系
命题 4.11 两个方程组同解的充要条件是其行向量组等价。
证明. 先证充分性。假设向量组 α
1
, α
2
, ··· , α
s
和 β
1
, β
2
, ··· , β
r
等价。向量组 α
1
, α
2
, ··· , α
s
对应的线性方程组如下:
a
11
x
1
+ a
12
x
2
+ ··· + a
1n
x
n
= m
1
a
21
x
1
+ a
22
x
2
+ ··· + a
2n
x
n
= m
2
.
.
.
a
s1
x
1
+ a
s2
x
2
+ ··· + a
sn
x
n
= m
s
(A
1
)
(A
2
)
.
.
.
(A
s
)
(A)
各个方程所对应的向量分别是
α
1
= (a
11
, a
12
, ··· , a
1n
, m
1
) (A
1
)
α
2
= (a
21
, a
22
, ··· , a
2n
, m
2
) (A
2
)
.
.
.
α
s
= (a
s1
, a
s2
, ··· , a
sn
, m
s
) (A
s
)
而向量组 β
1
, β
2
, ··· , β
s
对应的线性方程组为:
b
11
x
1
+ b
12
x
2
+ ··· + b
1n
x
n
= c
1
b
21
x
1
+ b
22
x
2
+ ··· + b
2n
x
n
= c
2
.
.
.
b
r1
x
1
+ b
r2
x
2
+ ··· + b
rn
x
n
= c
r
(B
1
)
(B
2
)
.
.
.
(B
r
)
(B)
向量组 β
1
, β
2
, ··· , β
r
中任意一个向量 β
i
都是 α
1
, α
2
, ··· , α
s
的线性组合,当且仅当方程 (B
i
)
是方程 (A
1
), ( A
2
), ··· , (A
s
) 的线性组合。即以下两个等式一定会同时成立:
β
i
= l
1
α
1
+ l
2
α
2
+ ··· + l
s
α
s
(B
i
) = l
1
(A
1
) + l
2
(A
2
) + ··· + l
s
(A
s
)
(1)
由等量公理可知,方程组的初等变换不会改变解,因此,方程组 (A
1
), ( A
2
), ··· , (A
s
) 的解一定
满足 (B
i
),即方程组 (A) 的解是方程组 (B) 的解。类似地,反过来亦可证明方程组 (B) 的解亦
是方程组 (A) 的解。
再证必要性。因为方程组 (A) 和 (B) 同解,所以将方程 (B
i
) 加入方程组 (A) 中,并不会改
变 (A) 的解。因此,方程 (B
i
) 对于方程组 (A) 来说,实际上是一个无效方程,即 (B
i
) 可通过
(A) 中的方程进行初等变换消去,亦即有 (1) 成立。因此,向量组 β
1
, β
2
, ··· , β
r
中每一个向量
都可以被 α
1
, α
2
, ··· , α
s
线性表出。同理可知,向量组 α
1
, α
2
, ··· , α
s
中每一个向量都可以被
β
1
, β
2
, ··· , β
r
线性表出,因此,两向量组等价。
实际上,上述必要性的证明过程不是很严谨。我们可以通过简约列梯形式的唯一性来严格
证明充分性。
线性方程组的简约型阶梯方程组是唯一的,且同解的线性方程组的简约型阶梯方程组是相
同的(因为简约型阶梯方程组相当于直接给出了解,所以简约型阶梯方程组不同,则不同
解)。
简约型阶梯方程组的行向量与原线性方程组的行向量组是等价的。若两个方程组同解,则
它们有相同的简约型阶梯方程组。由向量组等价的传递性可知,这两个方程组的行向量组
也是等价的。
58
4.4 线性相关与线性方程组的有解判别
4.4 线性相关与线性方程组的有解判别
设线性方程组为
a
11
x
1
+ a
12
x
2
+ ··· + a
1n
x
n
= b
1
a
21
x
1
+ a
22
x
2
+ ··· + a
2n
x
n
= b
2
.
.
.
a
s1
x
1
+ a
s2
x
2
+ ··· + a
sn
x
n
= b
s
其列向量为
α
1
=
a
11
a
21
.
.
.
a
s1
α
2
=
a
12
a
22
.
.
.
a
s2
··· α
n
=
a
1n
a
2n
.
.
.
a
sn
β =
b
1
b
2
.
.
.
b
s
于是线性方程组可以改写成(列)向量形式
x
1
α
1
+ x
2
α
2
+ ··· + x
n
α
n
= β
那么,2.2节的内容(解的情况及其判别准则)可以等价描述如下:
1. 方程组无解,若向量 β 无法由列向量组 α
1
, α
2
, ··· , α
n
线性表出。
2. 方程组有解,若向量 β 可以由列向量组 α
1
, α
2
, ··· , α
n
线性表出。由定理4.2:线性表示
的唯一性,又分为如下两种情况:
(a) 有唯一解,若列向量组 α
1
, α
2
, ··· , α
n
线性无关。
(b) 有无穷解,若列向量组 α
1
, α
2
, ··· , α
n
线性相关。
59
4.4 线性相关与线性方程组的有解判别
60
第五章 矩阵初步
定义5.1 矩阵: A 是数域 P 上一个 s × n 矩阵,它是由 s × n 个数 a
ij
(a
ij
∈ P ) 排成 s 行 n 列
的数表:
A =
a
11
a
12
··· a
1n
a
21
a
22
··· a
2n
.
.
.
.
.
.
.
.
.
a
s1
a
s2
··· a
sn
通常用加粗的大写拉丁字母表示,亦记为 A
s×n
。A 的每一列是一个 s 元有序数组,它是 P
s
中
的一个列向量,A 的所有列称为 A 的列向量组;同样地,A 的每一行是 P
n
中的一个行向量,
A 的所有行称为 A 的行向量组。
◦ a
ij
为矩阵的第 i 行、第 j 列,称为矩阵 A 的元素
◦ 以 a
ij
为 (i, j) 元的 s × n 矩阵可简记为 A = (a
ij
) 或 A = (a
ij
)
s×n
◦ 元素是实数的矩阵称为实矩阵;元素是复数的矩阵称为复矩阵
定义5.2 M
s×n
(P ): 元素全为 0 的矩阵称为零矩阵,记作 0,数域 P 上所有 s × n 矩阵组成的
集合记作 M
s×n
(P ),当 s = n 时,简记作 M
n
(P )。
5.1 矩阵的秩
矩阵由向量组成。如果把矩阵的每一行看成一个向量,那么矩阵就可以认为是由这些向量组成
的。同样,如果把每一列看成一个向量,那么矩阵也可以认为是由列向量组成的。由此可以定义
矩阵的秩。
定义5.3 矩阵的秩: 矩阵的行向量组的秩称为矩阵的行秩;矩阵的列向量组的秩称为矩阵的列
秩。
举一个例子,有如下矩阵:
A =
1 1 3 1
0 2 −1 4
0 0 0 5
0 0 0 0
那么,A 的行向量组是 α
1
= (1, 1, 3, 1), α
2
= (0, 2, −1, 4), α
3
= (0, 0, 0, 5), α
4
= (0, 0, 0, 0),它
的秩是 3。它的列向量组是 β
1
= (1, 0, 0, 0)
′
, β
2
= (1, 2, 0, 0)
′
, β
3
= (3, −1, 0, 0)
′
, β
4
= (1, 4, 5, 0)
′
。
它的秩也是 3。
自然地,提出一个问题,矩阵的行秩是否一定等于列秩?
61
5.1 矩阵的秩
引理 5.1
如果齐次线性方程组
a
11
x
1
+ a
12
x
2
+ ··· + a
1n
x
n
= 0
a
21
x
1
+ a
22
x
2
+ ··· + a
2n
x
n
= 0
.
.
.
a
s1
x
1
+ a
s2
x
2
+ ··· + a
sn
x
n
= 0
的系数矩阵的行秩 r < n,那么它有非零解(即无穷解)。
证明. 齐次线性方程组的系数矩阵和增广矩阵的行秩显然是一样的。因此,若其系数矩阵的行秩
r < n,则增广矩阵的行秩 r
a
< n。又因为,增广矩阵的行向量组和它的极大线性无关组是等价
的,所以它们对应的方程组同解。由定理2.2可知极大线性无关组对应的方程组存在非零解,因
此,行向量组对应的齐次线性方程组也存在非零解。引理成立。
定理 5.1
矩阵的行秩与列秩相等。
证明. 要证明行秩 = 列秩,只需证明行秩 ≥ 列秩,同时行秩 ≤ 列秩。
因为行向量和列向量只有写法上的不同,本质上没有区别。这启示我们可以对矩阵的行向量组
和列向量组分别应用引理5.1,从而证明行秩 ≥ 列秩,同时行秩 ≤ 列秩。
设所讨论的矩阵为 A,其行秩为 r,列秩为 r
1
:
A =
a
11
a
12
··· a
1n
a
21
a
22
··· a
2n
.
.
.
.
.
.
.
.
.
a
s1
a
s2
··· a
sn
先证 r ⩽ r
1
。以 α
1
, α
2
, ··· , α
s
代表矩阵 A 的行向量组,不妨设 α
1
, ··· , α
r
是它的一个极大
线性无关组。因为 α
1
, ··· , α
r
是线性无关的,所以下述方程只有零解:
x
1
α
1
+ ··· + x
r
α
r
= 0
也就是说,以下齐次线性方程组只有零解。
a
11
x
1
+ a
21
x
2
+ ··· + a
r1
x
r
= 0
a
12
x
1
+ a
22
x
2
+ ··· + a
r2
x
r
= 0
···
a
1n
x
1
+ a
2n
x
2
+ ··· + a
rn
x
r
= 0
由引理5.1,这个方程组的系数矩阵
a
11
a
21
··· a
r1
a
12
a
22
··· a
r2
.
.
.
.
.
.
.
.
.
.
.
.
a
1n
a
2n
··· a
rn
的行秩 ⩾ r。因此,在它的行向量中可以找到 r 个是线性无关的,譬如说,以下向量组线性无关。
(a
11
, a
21
, ··· , a
r1
) , (a
12
, a
22
, ··· , a
r2
) , ··· , (a
1r
, a
2r
, ··· , a
rr
)
根据命题4.4,在这些向量上添上几个分量后所得的向量组
(a
11
, a
21
, ··· , a
r1
, ··· , a
s1
) , (a
12
, a
22
, ··· , a
r2
, ··· , a
s2
) , ··· ,
(a
1r
, a
2r
, ··· , a
rr
, ··· , a
sr
)
也线性无关。它们正好是矩阵 A 的 r 个列向量,由它们的线性无关性可知矩阵 A 的列秩 r
1
至
少是 r, 也就是说 r
1
⩾ r。
62
5.1 矩阵的秩
用同样的方法可证 r ⩾ r
1
。这样就证明了矩阵的行秩与列秩相等。
因为矩阵的行秩等于列秩,所以统称为矩阵的秩。事实上,证明矩阵的行秩与列秩相等不止上述
一个方法。容易看出,矩阵的行、列向量组是存在关联或制约的,即:行向量的维度是列向量的
个数,反之,列向量的维度是行向量的个数。根据前面的命题:n + 1 个 n 维向量一定线性相关,
容易猜到矩阵的行秩和列秩应该是相等的。由此得到一个简单的证明如下。
证明. 该证明用到如下两个前提条件:
1. n + 1 个 n 维向量一定线性相关。(见55页)
2. 初等变换不会改变矩阵的秩。(见??页)
由于前提条件 1 可得到:对于一个 m × n 的矩阵 A 来说,它的行秩和列秩一定小于或等于
min(m, n) 。
假设矩阵 A 的行秩为 r(r ≤ min( m, n)),换而言之,其中有 m − r 个行向量可以被 r 个线性无
关的行向量线性表出。因此,对 A 做初等行变换,将其中 m − r 行全部化为 0,此时的矩阵记
为 B。由条件 2 可知,矩阵 A
m×n
和 B
r×n
的行秩和列秩是相等的。矩阵 B 的列秩 r
1
不可能
大于 r,因为第 r
1
+ 1 行到第 m 行都是 0 向量了,即此时列向量的维度为 r。
假设此时 r
1
不等于 r,即 r > r
1
。那么继续对 B 做初等列变换,会使得不全为 0 的列的个数
为 r
1
,将此时的矩阵记为 C
r×r
1
。这时,行向量非零行的个数 r 大于每个行向量的有效维数 r
1
。
显然,此时行向量组是线性相关的,这与前面假设行秩为 r 矛盾。
综上易知,行秩
r
一定要等于列秩
r
1
。
定理 5.2
n × n 矩阵的行列式为 0 的充要条件是矩阵的秩小于 n。
证明. 先证充分性。因为矩阵 A
n×n
的秩小于 n,所以 A 的 n 个行向量是线性相关的。当
n = 1 时,A 只有一个数,即只有一个一维向量,它又是线性相关的向量组,就是零向量,从而
|A| = |0| = 0。当 n > 1 时,矩阵 A 中有一行是其余各行的线性组合。根据行列式的性质(某
一行的倍数加到另一行,行列式不变),这一行可通过其余行的线性组合消去,即这一行就全变
成零,再由行列式的性质可知 |A| = 0。
再通过数学归纳法证明必要性。当 n = 1 时,由 |A| = 0 可知 A 仅有的一个元素就是零,因而
A 的秩为零。
假设结论对 n −1 级矩阵成立。现在来看 n 级矩阵的情况。我们以 α
1
, α
2
, ··· , α
n
代表 A 的行
向量。检查 A 的第一列元素,若它们全为零,则 A 的列向量组含有零向量,其秩必然小于 n。
若第一列元素的 n 个元素中至少有一个不为零,不妨假设 a
11
不为零。那么第二行到第 n 行减
去第一行的恰当的倍数,可以把 a
21
, a
31
, ··· , a
n1
消成零。
|
A
|
=
a
11
a
12
··· a
1n
a
21
a
22
··· a
2n
.
.
.
.
.
.
.
.
.
a
n1
a
n2
··· a
nn
=
a
11
a
12
··· a
1n
0 a
′
22
··· a
′
2n
.
.
.
.
.
.
.
.
.
0 a
′
n2
··· a
′
nn
= a
11
a
12
···
a
1n
a
′
22
··· a
′
2n
.
.
.
.
.
.
a
′
n2
··· a
′
nn
其中
(0, a
′
i2
, ··· , a
′
in
) = α
i
−
a
i1
a
11
α
1
, i = 2, ··· , n
因为 |A| = 0 且 a
11
不为 0,所以下面的 n − 1 级矩阵的行列式为零。
a
12
··· a
1n
a
′
22
··· a
′
2n
.
.
.
.
.
.
a
′
n2
··· a
′
nn
63
5.1 矩阵的秩
这也就是说,以下向量组是线性相关的:
α
2
−
a
i1
a
11
α
1
, ··· , α
n
−
a
i1
a
11
α
1
换而言之,有不全为零的数 k
2
, ··· , k
n
使得
k
2
(α
2
−
a
21
a
11
)α
1
+ ··· + k
n
(α
n
−
a
n1
a
11
α
1
) = 0
改写为下式
−(
a
21
a
11
k
2
+ ··· +
a
n1
a
11
k
n
)α
1
+ k
2
α
2
+ ··· + k
n
α
n
= 0
显然,−(
a
21
a
11
k
2
+ ··· +
a
n1
a
11
k
n
), k
2
, ··· , k
n
这组数也不全为零,因此向量组 α
1
, α
2
, ··· , α
n
线性
相关,它的秩小于 n。根据归纳法原理,必要性得证。
推断 5.2-1 齐次线性方程组
a
11
x
1
+ a
12
x
2
+ ··· + a
1n
x
n
= 0
a
21
x
1
+ a
22
x
2
+ ··· + a
2n
x
n
= 0
.
.
.
a
n1
x
1
+ a
n2
x
2
+ ··· + a
nn
x
n
= 0
有非零解的充要条件是它的系数矩阵的行列式为 0。
证明. 由定理5.2和引理5.1可证明充分性。由克拉默法则的推论2.3-1可得出条件的必要性。
定义5.4 矩阵的 k 级子式: 在一个 s × n 矩阵 A 中任意选定 k 行和 k 列(k ≤ min(s, n)),位
于这些选定的行和列的交点上的 k
2
个元素按原来的次序所组成的 k 级行列式,称为 A 的一个
k 级子式。
定理 5.3
一个 s × n 矩阵的秩是 r 的充要条件是:矩阵中有一个 r 级子式不为零,同时所有 r + 1
级子式全为零。
这个定理实际上包含两部分:
1. 矩阵 A 的秩 ⩾ r 的充分必要条件为 A 有一个 r 级子式不为零
2. 矩阵 A 的秩 ⩽ r 的充分必要条件为 A 的所有 r + 1 级子式全为零
有时候,这两个结论可以分开来用(以下的证明正是如此)。
证明. 由定理5.2和 r 级子式的定义可知必要性成立,即可以从矩阵中取出这样的 r 级子式。
再证充分性。设在矩阵 A 中有一 r 级子式不为零, 而所有 r+ 1 级子式全为零。我们证明 A 的
秩为 r。首先我们指出, 由行列式按一行展开的公式可知, 如果 A 的 r + 1 级子式全为零, 那么
A 的 r + 2 级子式也一定为零, 从而 A 的所有级数大于 r 的子式全为零。设 A 的秩为 t。由必
要性, t 不能小于 r, 否则 A 的 r 级子式就全为零了。同样, t 也不能大于 r, 否则 A 就要有一个
t(⩾ r + 1) 级子式不为零, 而按照假定这是不可能的。因此 t = r, 这就是我们要证明的结论。
到目前为止,我们还未介绍求解秩的方法,但基于上述定理,以及初等变换不会改变矩阵的秩这
两点,我们可以得到启发:通过初等变换,将矩阵 A 转换为阶梯形矩阵,而阶梯形矩阵的秩就
等于其中非零行的数目。
设 A 是一阶梯形矩阵,不为零的行数是 r。
64

5.2 线性方程组有解判别定理 (下)
A =
a
11
a
12
··· a
1r
··· a
1n
0 a
22
··· a
2r
··· a
2n
.
.
.
.
.
.
.
.
.
.
.
.
0 0 ··· a
rr
··· a
rn
0 0 ··· 0 ··· 0
.
.
.
.
.
.
.
.
.
.
.
.
0 0 ··· 0 ··· 0
其中 a
ii
6= 0, i = 1, 2, ··· , r。不难验证,所有矩阵都可以通过初等变换转换为类似 A 的阶梯形
矩阵。根据行列式的递归展开式,显然,
A
的左上角的
r
级子式为
a
11
a
12
··· a
1r
0 a
22
··· a
2r
.
.
.
.
.
.
.
.
.
0 0 ··· a
rr
= a
11
a
22
···a
rr
6= 0
又因为 A 的所有 r + 1 级子式都含有零向量,所以 A 的所有 r + 1 级子式全为零。因此,A 的
秩为 r。
实际上,就算不使用定理5.3,我们也能证明 A 的秩为 r。对 A 继续作初等行变换,将其转换为
简约列梯矩阵。
A =
a
11
a
12
··· a
1r
··· a
1n
0 a
22
··· a
2r
··· a
2n
.
.
.
.
.
.
.
.
.
.
.
.
0 0 ··· a
rr
··· a
rn
0 0 ··· 0 ··· 0
.
.
.
.
.
.
.
.
.
.
.
.
0 0 ··· 0 ··· 0
5.2 线性方程组有解判别定理 (下)
如下线性方程组
a
11
x
1
+ a
12
x
2
+ ··· + a
1n
x
n
= b
1
a
21
x
1
+ a
22
x
2
+ ··· + a
2n
x
n
= b
2
···
a
s1
x
1
+ a
s2
x
2
+ ··· + a
sn
x
n
= b
s
可以表示为列向量的线性组合:x
1
α
1
+ x
2
α
2
+ ··· + x
n
α
n
= β。其中
α
i
=
a
1i
a
2i
.
.
.
a
si
i = (1, 2, ··· , n) β =
b
1
b
2
.
.
.
b
s
那么,线性方程组有解的充要条件为向量 β 可以表成向量组 α
1
, α
2
, ··· , α
n
的线性组合。这是
在4.4节提到的内容。用秩的概念,这个命题可以等价叙述如下:
定理 5.4. 线性方程组有解判别定理
线性方程组有解的充要条件为它的系数矩阵与增广矩阵有相同的秩。
证明. 先证必要性,设以上线性方程组有解,即 β 可以经向量组 α
1
, α
2
, ··· , α
n
线性表出。由
此立即推出,向量组 α
1
, α
2
, ··· , α
n
与向量组 α
1
, α
2
, ··· , α
n
, β 等价,因而有相同的秩。这两
65

5.3 矩阵的运算
个向量组分别是系数矩阵与增广矩阵的列向量组。因此,两矩阵有相同的秩。
再证充分性。设系数矩阵与增广矩阵有相同的秩,也就是说, 它们的列向量组 α
1
, α
2
, ··· , α
n
与
α
1
, α
2
, ··· , α
n
, β 有相同的秩,令它们的秩为 r。α
1
, α
2
, ··· , α
n
中的极大线性无关组由 r 个向
量组成,不妨设 α
1
, α
2
, ··· , α
r
是它的一个极大线性无关组。显然 α
1
, α
2
, ··· , α
r
也是向量组
α
1
, α
2
, ··· , α
n
, β 的一个极大线性无关组,因此向量 β 可以经 α
1
, α
2
, ··· , α
r
线性表出。既然
β 可以经 α
1
, α
2
, ··· , α
r
线性表出,当然它可以经 α
1
, α
2
, ··· , α
n
线性表出。因此,方程组有
解。
5.3 矩阵的运算
定义5.5 同型矩阵: 具有相同行数和列数的矩阵称为同型矩阵。
定义5.6 零矩阵: 所有元素都为 0 的矩阵称为零矩阵,记为 O。
定义5.7 相等的矩阵: 数域 P 上两个矩阵 A, B,如果它们的行数相等,列数也相等,并且它们
的所有元素对应相等 (即 A 的 (i, j) 元等于 B 的 (i, j) 元),那么称 A 与 B 相等,记作 A = B。
定义5.8 矩阵的加法: 对于同型矩阵 A 和 B,它们的加法定义为对应元素相加。
A + B = (a
ij
)
s×n
+ (b
ij
)
s×n
= (a
ij
+ b
ij
)
s×n
a
11
a
12
··· a
1n
a
21
a
22
··· a
2n
.
.
.
.
.
.
.
.
.
.
.
.
a
s1
a
s2
··· a
sn
+
b
11
b
12
··· b
1n
b
21
b
22
··· b
2n
.
.
.
.
.
.
.
.
.
.
.
.
b
s1
b
s2
··· b
sn
=
a
11
+ b
11
a
12
+ b
12
··· a
1n
+ b
1n
a
21
+ b
21
a
22
+ b
22
··· a
2n
+ b
2n
.
.
.
.
.
.
.
.
.
.
.
.
a
s1
+ b
s1
a
s2
+ b
s2
··· a
sn
+ b
sn
显然,加法满足以下性质:
1. 交换律:A + B = B + A
2. 结合律:(A + B) + C = A + (B + C)
3. 存在单位元:A + O = A
利用 A, B 和 A + B 的各个列向量组的极大线性无关组间的线性表出关系,容易证明以下不等
式。
秩(A + B) ⩽ min 秩(A) + 秩(B)
证明. 令 A = (A
1
, A
2
, ··· , A
n
) , B = (B
1
, B
2
, ··· , B
n
) , A
i
, B
j
(i, j = 1, 2, ··· , n) 都是列向量。
A+B = (A
1
+ B
1
, ··· , A
n
+ B
n
),它的每个列向量都可由列向量组 {A
1
, ··· , A
n
, B
1
, ··· , B
n
}
线性表出。又设 {A
i
1
, ··· , A
i
r
} 及 {B
j
1
, ··· , B
j
s
} 分别是 {A
1
, ··· , A
n
} 和 {B
1
, ··· , B
n
} 的极
大线性无关组。则 {A
1
+ B
1
, ··· , A
n
+ B
n
} 都可由向量组 {A
i
1
, ··· , A
i
r
, B
j
1
, ··· , B
j
s
} 线性
表出。故
秩(A + B) = 秩 {A
1
+ B
1
, ··· , A
n
+ B
n
}
⩽ 秩 {A
i
1
, ··· , A
i
r
, B
j
1
, ··· , B
j
s
}
⩽ r + s
即:秩(A + B) ⩽ 秩(A) + 秩(B)
定义5.9 矩阵的数量乘法: kA = k(a
ij
)
s×n
= (ka
ij
)
s×n
k
a
11
a
12
··· a
1n
a
21
a
22
··· a
2n
.
.
.
.
.
.
.
.
.
.
.
.
a
s1
a
s2
··· a
sn
=
ka
11
ka
12
··· ka
1n
ka
21
ka
22
··· ka
2n
.
.
.
.
.
.
.
.
.
.
.
.
ka
s1
ka
s2
··· ka
sn
66

5.3 矩阵的运算
设 k,l 为常数,A 和 B 为同型矩阵。矩阵的数乘有如下性质:
1. (k + l)A = kA + lA
2. k(lA) = (kl)A = l(kA)
3. k(A + B) = kA + kB
4. 1A = A
5. k(AB) = (kA)B = A(kB)
定义5.10 负矩阵: 对矩阵 A 的所有元素都取负,得到的新矩阵称为 A 的负矩阵,记为 −A。显
然,A + (−A) = O。
定义5.11 矩阵的减法: 对于同型矩阵 A 和 B,它们的减法定义为对应元素相减。
A − B = A + (−B) = (a
ij
)
s×n
− (b
ij
)
s×n
= (a
ij
− b
ij
)
s×n
a
11
a
12
··· a
1n
a
21
a
22
··· a
2n
.
.
.
.
.
.
.
.
.
.
.
.
a
s1
a
s2
··· a
sn
−
b
11
b
12
··· b
1n
b
21
b
22
··· b
2n
.
.
.
.
.
.
.
.
.
.
.
.
b
s1
b
s2
··· b
sn
=
a
11
− b
11
a
12
− b
12
··· a
1n
− b
1n
a
21
− b
21
a
22
− b
22
··· a
2n
− b
2n
.
.
.
.
.
.
.
.
.
.
.
.
a
s1
− b
s1
a
s2
− b
s2
··· a
sn
− b
sn
定义5.12 矩阵的乘法: 对矩阵 A
s×n
= (a
ij
)
s×n
和矩阵 B
n×m
= (b
ij
)
n×m
,我们定义
A
s×n
B
n×m
= C
s×m
= (c
ij
)
s×m
其中 c
ij
=
n
P
k=1
a
ik
b
kj
。
由矩阵乘法的定义,以及连加号可交换次序,不难证明矩阵乘法满足以下性质:
1. 结合律:(AB)C = A(BC)
2. 乘法对加法右分配律:(A + B)C = AC + BC
3. 乘法对加法左分配律:C(A + B) = CA + CB
注意的是,以上第 2 和第 3 个运算性质不是同时成立的,因为根据矩阵乘法的定义可看出,矩
阵乘法不符合交换律。一方面,当 AB 有定义时,BA 不一定有定义;另一方面,即使 AB 和
BA 都有定义,AB 和 BA 的级数不一定相等;即使 A 和 B 都是 n 级方阵,AB 和 BA 的
级数相等,AB 和 BA 也不一定相等。
设 A =
1 0
0 0
,B =
0 0
0 1
, 则 AB = O。
这个例子说明,两个不为零的矩阵的乘积可以是零,即对于矩阵乘法,从 AB = O 不能推出
A = O 或 B = O。由此,可知矩阵乘法的消去律也不成立,即从 AB = AC 和 A 6= O 不能
推出 B = C。
设矩阵 A
s×n
= (a
ij
) 的列向量组为 α
1
, α
2
, ··· , α
n
,矩阵 B
n×m
= b
ij
的行向量组为 γ
1
, γ
2
, ··· , γ
n
,
则 A 和 B 可以分别记为
A = (α
1
, α
2
, ··· , α
n
) B =
γ
1
γ
2
.
.
.
γ
n
根据矩阵乘法的定义,AB 乘积
67
5.3 矩阵的运算
AB =
a
11
a
12
··· a
1n
a
21
a
22
··· a
2n
.
.
.
.
.
.
.
.
.
a
s1
a
s2
··· a
sn
b
11
b
12
··· b
1m
b
21
b
22
··· b
2m
.
.
.
.
.
.
.
.
.
b
n1
b
n2
··· b
nm
的第 j 列可以表示为 A 的列向量的线性组合
a
11
b
1j
+ a
12
b
2j
+ ··· + a
1n
b
nj
a
21
b
1j
+ a
22
b
2j
+ ··· + a
2n
b
nj
.
.
.
a
s1
b
1j
+ a
s2
b
2j
+ ··· + a
sn
b
nj
= b
1j
α
1
+ b
2j
α
2
+ ··· + b
nj
α
n
因此
AB = (α
1
, α
2
, ··· , α
n
)
b
11
b
12
··· b
1m
b
21
b
22
··· b
2m
.
.
.
.
.
.
.
.
.
b
n1
b
n2
··· b
nm
= (b
11
α
1
+ b
21
α
2
+ ··· + b
n1
α
n
, ··· , b
1m
α
1
+ b
2m
α
2
+ ··· + b
nm
α
n
)
这是矩阵乘法的第二种表述方式。类似地,矩阵乘积 AB 也可以用 B 的行向量表示
AB =
a
11
a
12
··· a
1n
a
21
a
22
··· a
2n
.
.
.
.
.
.
.
.
.
a
s1
a
s2
··· a
sn
γ
1
γ
2
.
.
.
γ
n
=
a
11
γ
1
+ a
12
γ
2
+ ··· + a
1n
γ
n
a
21
γ
1
+ a
22
γ
2
+ ··· + a
2n
γ
n
.
.
.
a
s1
γ
1
+ a
s2
γ
2
+ ··· + a
sn
γ
n
这是矩阵乘法的第三种表述方式。
定义5.13 单位矩阵: 主对角线上的元素全是 1,其余元素全是 0 的 n × n 矩阵
1 0 ··· 0
0 1 ··· 0
.
.
.
.
.
.
.
.
.
0 0 ··· 1
称为 n 级单位矩阵,记为 E
n
,或者在不致引起混乱的时候简单记作 E 。
显然有
A
sn
E
n
= A
sn
,
E
s
A
sn
= A
sn
.
定义5.14 矩阵的幂次: 设 A 是一 n × n 矩阵,k 为任意正整数,定义
A
1
= A
A
k+1
= A
k
A
换句话说, A
k
就是 k 个 A 连乘。
显然,方幂只能对行数与列数相等的矩阵来定义。由乘法的结合律,不难证明
A
k
A
l
= A
k+l
A
k
l
= A
kl
因为矩阵乘法不适合交换律,因此 (AB)
k
和 A
k
B
k
一般不相等。
定义5.15 矩阵的转置: 对一个 s × n 的矩阵 A,将它的行和列的位置交换,即将第 i 行第 j 列
68

5.4 矩阵乘积的行列式与秩
的元素放在第 j 行第 i 列,得到新的 n ×s 矩阵,称为矩阵 A 的转置,记为 A
T
或 A
′
。
因此,如果 A = (a
ij
)
s×n
,A
T
= (b
ij
)
n×s
,则有 b
ij
= a
ji
。
A =
a
11
a
12
··· a
1
n
a
21
a
22
··· a
2n
.
.
.
.
.
.
.
.
.
.
.
.
a
s1
a
s2
··· a
sn
A
T
=
a
11
a
21
··· a
s
1
a
12
a
22
··· a
s2
.
.
.
.
.
.
.
.
.
.
.
.
a
1n
a
2n
··· a
sn
关于矩阵的转置,我们有下列性质:
1. (A
T
)
T
= A
2. (A + B)
T
= A
T
+ B
T
3. (kA)
T
= kA
T
4. (AB)
T
= B
T
A
T
5.4 矩阵乘积的行列式与秩
定理 5.5
设 A, B 是数域 P 上的两个 n × n 矩阵, 那么
|AB| = |A||B|
即矩阵乘积的行列式等于它的因子的行列式的乘积。
证明该定理常见的方法有如下三种:
1. 将 A 表示成基本矩阵乘积,透过 det(EB) = (det E)(det B) 得证,其中 E 是任意基本矩
阵。
2. 基于分块矩阵运算的简明证法。
3. 第三种方式则建立于函数 d(A) = det(AB)/ det B 之上。
这里另外列出两种证明方法。按照一般的想法,理论上,直接根据矩阵乘积的定义和行列式的定
义写出 |AB| 的展开式,再根据行列式的性质,将其凑出 |A||B| 的形式即可。从表面上看,直
接计算矩阵乘积及其行列式似乎涉及一定程度的蛮力,而矩阵乘积的行列式展开式十分繁复,看
起来更加可怕。
天下无难事,只怕有心人。我们不要被表象所蒙蔽了,关键其实在怎么乘而已。行列式的英文是
determinant,意为判定,它的主要的功用之一在于判定矩阵是否可逆。大家有没有想过:为什
么 determinant 要译成行列式呢?矩阵的日文是行列,行列式可能源自日文,意为矩阵式。行列
式这个名词提示了它所具备的三个基本性质全都建立于矩阵的行或列之上。计算行列式时,我
们应该尽量以行或列为单位,而非中学时习惯使用的元。
证明. 将矩阵 A 和 B 用列向量表示(使用行向量的表示形式亦可):
A =
a
1
a
2
··· a
n
, B =
b
1
b
2
··· b
n
根据矩阵乘法规则和向量加法规则:
AB = A
b
1
b
2
··· b
n
=
Ab
1
Ab
2
··· Ab
m
其中
69

5.4 矩阵乘积的行列式与秩
Ab
p
=
a
1
a
2
··· a
n
b
1p
b
2p
.
.
.
b
np
= b
1p
a
1
+ b
2p
a
2
+ ··· + b
np
a
n
, p = 1 , 2, ··· , n
以上等式可能初看起来显得突兀,但不难验证它是成立的。了解矩阵分块乘法之后,上式会变得
直观。利用行列式的多线性、交错性和斜对称性,详细推导过程如下:
det(AB) =
Ab
1
Ab
2
··· Ab
m
=
P
n
i
=1
b
i1
a
i
P
n
j
=1
b
j2
a
j
···
P
n
k
=1
b
kn
a
k
=
n
X
i=1
n
X
j=1
···
n
X
k=1
b
i1
a
i
b
j2
a
j
··· b
kn
a
k
(多线性函数)
=
n
X
i
1
=1
n
X
j=1
···
n
X
k=1
b
i1
b
j2
···b
kn
a
i
a
j
···
a
k
(多线性函数)
=
X
(i,j,···,k)
b
i1
b
j2
···b
kn
a
i
a
j
··· a
k
(交错性)
=
X
(i,j,···,k)
b
i1
b
j2
···b
kn
det P
(i,j,···,k)
a
i
a
j
··· a
k
(斜对称性)
= (det A)
X
(i,j,···,k)
b
i1
b
j2
···b
kn
det P
(i,j,···,k)
= (det A)(det B)
上式中,(i, j, ··· , k) 代表数字 1, 2, ··· , n 所能组成的 n! 种可能序列。P
(i,j,···,k)
是对应列排序为
(i, j, ··· , k) 的排列矩阵,即有 det P
(i,j,···,k)
= det P
T
(i,j,···,k)
= (−1)
p
,p 代表从 (i, j, k) 至 (1, 2, 3)
所执行的置换运算次数。
上述证明思路初看繁复,实则简单直接。实际上,前面介绍的拉普拉斯定理也是一种元素分块相
乘的计算方法,利用拉普拉斯定理可以构造一个巧妙的证明。
证明. 假设 AB = C,A、B 和 C 分别是 n 级矩阵 A、B 和 C 的行列式。由矩阵乘法的定义
可知,C 或 C 的第 i 行、第 j 列的元素为 c
ij
=
n
P
k=1
a
ik
b
kj
。
用 A 和 B 的元素构造行列式 D
D =
a
11
a
12
··· a
1n
0 0 ··· 0
a
21
a
22
··· a
2n
0 0 ··· 0
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
a
n1
a
n2
··· a
nn
0 0 ··· 0
−1 0 ··· 0 b
11
b
12
··· b
1n
0 −1 ··· 0 b
21
b
22
··· b
2n
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
0 0 ··· −1 b
n1
b
n2
··· b
nn
根据拉普拉斯定理, 将 D 按前 n 行展开。则因 D 中前 n 行除去左上角那个 n 级子式外, 其余
的 n 级子式都等于零。所以
D =
a
11
a
12
··· a
1n
a
21
a
22
··· a
2n
.
.
.
.
.
.
.
.
.
a
n1
a
n2
··· a
nn
·
b
11
b
12
··· b
1n
b
21
b
22
··· b
2n
.
.
.
.
.
.
.
.
.
b
n1
b
n2
··· b
nn
= AB
现在来证 D = C。对 D 作初等行变换。将第 n + 1 行的 a
11
倍,第 n + 2 行的 a
12
倍, ···, 第
70

5.4 矩阵乘积的行列式与秩
2n 行的 a
1n
倍加到第一行, 得
D =
0 0 ··· 0 c
11
c
12
··· c
1n
a
12
a
22
··· a
2n
0 0 ··· 0
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
a
n1
a
n2
··· a
nn
0 0 ··· 0
−1 0 ··· 0 b
11
b
12
··· b
1
n
0 −1 ··· 0 b
21
b
22
··· b
2n
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
0 0 ··· −1 b
n1
b
n2
··· b
nn
再依次将第 n + 1 行的 a
k1
(k = 2, 3, ··· , n) 倍, 第 n + 2 行的 a
k2
倍, ···, 第 2n 行的 a
kn
倍加
到第 k 行, 就得
D =
0 0 ··· 0 c
11
c
12
··· c
1n
0 0 ··· 0 c
21
c
22
··· c
2n
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
0 0 ··· 0 c
n1
c
n2
··· c
nn
−1 0 ··· 0 b
11
b
12
··· b
1n
0 −1 ··· 0 b
21
b
22
··· b
2n
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
0 0 ··· −1 b
n1
b
n2
··· b
nn
这个行列式的前 n 行也只可能有一个 n 级子式不为零, 因此由拉普拉斯定理
D =
c
11
c
12
··· c
1n
c
21
c
22
··· c
2n
.
.
.
.
.
.
.
.
.
c
n1
c
n2
··· c
nn
· (−1)
(1+2+···+n)+(n+1+n+2+···+2n)
−1 0 ··· 0
0 −1 ··· 0
.
.
.
.
.
.
.
.
.
0 0 ··· −1
=
c
11
c
12
··· c
1n
c
21
c
22
··· c
2n
.
.
.
.
.
.
.
.
.
c
n1
c
n2
··· c
nn
· (−1)
(1+2n)n
· (−1)
n
=C
用数学归纳法,定理5.5不难推广到多个因子的情形。
推断 5.5-1 设 A
1
, A
2
, ··· , A
m
都是数域 P 上的 n × n 矩阵,于是
|A
1
A
2
···A
m
| = |A
1
||A
2
|···|A
m
|
定义5.16 退化矩阵: 数域 P 上的 n × n 矩阵 A 称为非退化的,若 | A |6= 0;否则称为退化的。
由定理5.2,显然,n ×n 级矩阵是非退化的充分必要条件是它的秩等于 n。从定理5.5,立刻推出:
推断 5.5-2 设 A, B 是数域 P 上 n × n 矩阵, 矩阵 AB 为退化的充分必要条件是 A, B 中至少
有一个是退化的。
定理 5.6
设 A 是数域 P 上 n × m 矩阵, B 是数域 P 上 m × s 矩阵, 于是
秩(AB) ⩽ min[ 秩(A) , 秩(B)]
即乘积的秩不超过各因子的秩。
证明. 设
71

5.5 矩阵的逆
A =
a
11
a
12
··· a
1m
a
21
a
22
··· a
2m
.
.
.
.
.
.
.
.
.
a
n1
a
n2
··· a
nm
, B =
b
11
b
12
··· b
1s
b
21
b
22
··· b
2s
.
.
.
.
.
.
.
.
.
b
m1
b
m2
··· b
ms
只需要证明秩 (AB) ⩽ 秩 (A), 同时 秩 (AB) ⩽ 秩 (B)。现在来分别证明这两个不等式。
令 B
1
, B
2
, ··· , B
m
表示 B 的行向量,C
1
, C
2
, ··· , C
n
表示 AB 的行向量。由计算可知,C
i
的
第 j 个分量和 a
i1
B
1
+ a
i2
B
2
+ ··· + a
im
B
m
的第 j 个分量都等于
P
m
k=1
a
ik
b
kj
,因而
C
i
= a
i1
B
1
+ a
i2
B
2
+ ··· + a
im
B
m
(i = 1, 2, ··· , n)
即矩阵 AB 的行向量组 C
1
, C
2
, ··· , C
n
可经 B 的行向量组线性表出。所以 AB 的秩不能超过
B 的秩 (参看命题4.9),也就是说,
秩(AB) ⩽ 秩(B)
同样,令 A
1
, A
2
, ··· , A
m
表示 A 的列向量,D
1
, D
2
, ··· , D
s
表示 AB 的列向量。由计算可知:
D
i
= b
1i
A
1
+ b
2i
A
2
+ ··· + b
mi
A
m
(i = 1, 2, ··· , s)
因此,矩阵
AB
的列向量组可以经矩阵
A
的列向量组线性表出,因而前者的秩不可能超过后者
的秩,即
秩(AB) ⩽ 秩(A)
用数学归纳法,上述定理不难推广到多个因子的情形。
推断 5.6-1 如果 A = A
1
A
2
···A
t
, 那么
秩(A) ⩽ min
1⩽j⩽t
秩 (A
j
)
5.5 矩阵的逆
矩阵与复数相仿,有加、减、乘三种运算。除此之外,复数还有除法运算,除法运算是乘法的逆
运算。那么矩阵的乘法是否也和复数一样有逆运算呢?
复数的除法可以通过倒数和乘法来定义,而一个复数 a 6= 0 的倒数 a
−1
可以用等式 aa
−1
= 1 来
刻画。我们知道,对于任意的 n 级方阵 A 都有 AE = EA = A,这里 E 是 n 级单位矩阵。因
之,从乘法的角度来看,n 级单位矩阵在 n 级方阵中的地位类似于 1 在复数中的地位。相仿地,
我们引入以下定义。
定义5.17 逆矩阵: n 级方阵 A 称为可逆的,如果有 n 级方阵 B,使得
AB = BA = E
这里 E 是 n 级单位矩阵。B 称为 A 的逆矩阵,记作 A
−1
。显然根据此定义,B 必然也是可逆
的,A 和 B 互为逆矩阵。
因为单位矩阵 E 是方阵,对于同一个 n 级单位矩阵 E,A 和 B 必须都是 n 级矩阵才有可能满
足 AB = BA = E,这点根据矩阵乘法规则即可验证。因此,这一节出现的所有矩阵,没有特
殊说明的情况下,默认都为 n 级方阵。
对于任意的矩阵 A ,如果它有逆矩阵,其逆矩阵 B 是唯一的。事实上,假设 B
1
, B
2
是 A 的逆
矩阵,就有
B
1
= B
1
E = B
1
(AB
2
) = (B
1
A) B
2
= EB
2
= B
2
72
5.5 矩阵的逆
下面要解决的问题是:在什么条件下矩阵 A 是可逆的?如果 A 可逆,怎样求 A
−1
?事实上,根
据拉普拉斯定理的推论,我们很容易构造出矩阵 A 的逆矩阵。
定义5.18 伴随矩阵: 设 A
ij
是矩阵
A =
a
11
a
12
··· a
1n
a
21
a
22
··· a
2n
.
.
.
.
.
.
.
.
.
a
n1
a
n2
··· a
nn
中元素 a
ij
的代数余子式,矩阵
A
∗
=
A
11
A
21
··· A
n1
A
12
A
22
··· A
n2
.
.
.
.
.
.
.
.
.
A
1n
A
2n
··· A
nn
称为 A 的伴随矩阵。
由行列式按一行 (列) 展开的公式立即得出
AA
∗
= A
∗
A =
d 0 ··· 0
0 d ··· 0
.
.
.
.
.
.
.
.
.
0 0 ··· d
= dE
其中 d = |A|。如果 d = |A| 6= 0,那么由上式可得
A
1
d
A
∗
=
1
d
A
∗
A = E (5.1)
由以上论述,马上可以得到以下定理。
定理 5.7
矩阵 A 是可逆的充分必要条件是 A 非退化,而
A
−1
=
1
d
A
∗
(d = |A| 6= 0)
证明. 先证明充分性。当 d = |A| 6= 0 时,由5.1式可知,A 可逆,且 A
−1
=
1
d
A
∗
。
再证必要性。如果 A 可逆,那么有 A
−1
使
AA
−1
= E
由矩阵乘积的行列式公式,即定理5.5,得
|A|
A
−1
= |E| = 1
因而
|
A
| 6
= 0
,即
A
非退化。
由 |A|
A
−1
= |
E
|
= 1
可以看出,若 |
A
|
=
d
6
= 0
,那么
A
−1
= d
−1
。
推断 5.7-1 如果矩阵 A, B 可逆,那么 A
′
与 AB 也可逆,且
A
′
−1
=
A
−1
′
(AB)
−1
= B
−1
A
−1
证明. 由定理5.7即得推论的前一半,现在来证后一半。由
AA
−1
= A
−1
A = E
73

5.5 矩阵的逆
两边取转置,有
A
−1
′
A
′
= A
′
A
−1
′
= E
′
= E
因此
A
′
−1
=
A
−1
′
(转置和求逆可交换次序)
由
(AB)
B
−1
A
−1
=
B
−1
A
−1
(AB) = E
即得
(AB)
−1
= B
−1
A
−1
定理 5.8
A 是一个 s × n 矩阵,如果 P 是 s × s 可逆矩阵,Q 是 n × n 可逆矩阵,那么
秩(A) = 秩(P A) = 秩(AQ)
证明. 令 B = P A,由定理5.6,
秩(B) ⩽ 秩(A) ;
又因为
P
−1
B = A
又有
秩(A) ⩽ 秩(B)
所以
秩(A) = 秩(B) = 秩(P A)
另一个等式可以同样地证明。
5.5.1 逆矩阵与线性方程求解
利用矩阵的逆,可以给出克拉默法则的另一种推导方法。对于如下线性方程组:
a
11
x
1
+ a
12
x
2
+ ··· + a
1n
x
n
= b
1
a
21
x
1
+ a
22
x
2
+ ··· + a
2n
x
n
= b
2
···
a
n1
x
1
+ a
n2
x
2
+ ··· + a
nn
x
n
= b
n
可以写出如下形式:
AX = B
其中
74

5.6 矩阵的分块乘法
A =
a
11
a
12
··· a
1n
a
21
a
22
··· a
2n
.
.
.
.
.
.
.
.
.
.
.
.
a
n1
a
n2
··· a
nn
X =
x
1
a
2
.
.
.
x
n
B =
b
1
b
2
.
.
.
b
n
如果 |A| 6= 0,那么 A 可逆。方程组的一个解:
X = A
−1
B
如果 X = C 也是方程组的一个解,那么由
AC = B
得
A
−1
(AC) = A
−1
B,
即
C = A
−1
B
这就是说,解 X = A
−1
B 是唯一的。由定理
5.7给出的公式,进一步可得:
X =
A
∗
|A|
B
这就是克拉默法则中给出的唯一解公式。
5.6 矩阵的分块乘法
设 A 为 n × m 矩阵, 按照 n
1
, n
2
, ··· , n
p
行, m
1
, m
2
, ··· , m, 列分块为
A =
A
11
··· A
1q
.
.
.
.
.
.
A
p1
··· A
pq
n
1
.
.
.
n
p
m
1
··· m
q
设 B 为 m × f 矩阵,对 B 作分块的方式不能任意,要求对 B 的行的分块方式和对 A 的列的
分块方式相同,即
B =
B
11
··· B
1r
.
.
.
.
.
.
B
q1
··· B
qr
m
1
.
.
.
m
q
s
1
··· s
r
所以 A
ij
为 n
i
× m
j
矩阵, B
jk
为 m
j
× s
k
矩阵。因此 A
ij
和 B
jk
可以相乘。且
AB =
A
11
··· A
1q
.
.
.
.
.
.
A
p1
··· A
pq
B
11
··· B
1r
.
.
.
.
.
.
B
q1
··· B
qr
=
q
P
j=1
A
1j
B
j1
···
q
P
j=1
A
1
j
B
jr
.
.
.
.
.
.
q
P
j=1
A
pj
B
j1
···
q
P
j=1
A
pj
B
jr
75
5.6 矩阵的分块乘法
证明. 事实上,
AB =
a
11
··· a
1m
.
.
.
.
.
.
a
n1
··· a
nm
b
11
··· b
1f
.
.
.
.
.
.
b
m1
··· b
mf
=
m
P
j=1
a
1j
b
j1
···
m
P
j=1
a
1j
b
jf
.
.
.
.
.
.
m
P
j=1
a
nj
b
j1
···
m
P
j=1
a
nj
b
jf
它可改写为
AB =
(a
11
···a
1m
)B
.
.
.
(a
n1
···a
nm
)B
=
a
11
··· a
1m
.
.
.
.
.
.
a
n
1
1
··· a
n
1
m
B
.
.
.
a
n
′
1
··· a
n
′
m
.
.
.
.
.
.
a
n1
··· a
nm
B
=
(A
11
···A
1q
)B
.
.
.
(A
p1
···A
pq
)B
其中 n
′
= n
1
+ ··· + n
p−1
+ 1。同理
AB =
A
11
··· A
1q
B
11
.
.
.
B
q1
···
A
11
··· A
1q
B
11
.
.
.
B
qr
.
.
.
.
.
.
A
11
··· A
pq
B
11
.
.
.
B
q1
···
A
11
··· A
pq
B
11
.
.
.
B
qr
因此,问题转化为证明
A
i1
··· A
iq
B
1l
.
.
.
B
ql
=
q
X
j=1
A
ij
B
jl
事实上,若能证明
C
(n,m
1
)
D
(n,m
2
)
E
(m
1
,f)
F
(m
2
,f)
= CE + DF
则
A
i1
··· A
iq
B
1l
.
.
.
B
ql
=
A
i1
A
i2
··· A
iq
B
1l
B
2l
.
.
.
B
ql
= A
i1
B
1l
+
A
i2
··· A
iq
B
2l
.
.
.
B
ql
= ··· =
q
X
j=1
A
ij
B
jl
76

5.7 初等矩阵
下面来证 (C D)
E
F
= CE + DF 。
取出 C 的第 i 行 (c
i1
···c
im
1
),D 的第 i 行 (d
i1
, ··· , d
im
2
);取出 E 的第 j 列, 排成横行为
e
1j
, ··· , e
m1
j
,F 的第 j 列,排成横行为 (f
1j
, ··· , f
m
2
j
)。于是 CE + DF 的第 i 行,第 j 列
元素为
m
1
X
k=1
c
ik
e
kj
+
m
2
X
k=1
d
ik
f
kj
而 (C D) 的第 i 行为 (c
i1
, ··· , c
im
1
, d
i1
, ··· , d
im
2
),
E
F
的第 j 列排成行为 (e
1j
, ··· , e
m
1
j
,
f
1j
, ··· , f
m
2
j
),于是 (C D)
E
F
的第 i 行第 j 列元素为
c
i1
e
1j
+ ··· + c
im
1
e
m
1
j
+ d
i1
f
1j
+ ··· + d
im
2
f
m
2
j
这证明了 CE +DF 和 (C D)
E
F
的任意相同位置元素相等,即 (C D)
E
F
= CE +
DF 。至此,已经完全证明了分块矩阵的乘法公式。
以上叙述告诉我们,对分块矩阵作乘法,相当于把每一块当作个元索,按通常矩阵乘法的定义作
运算。这一特点是使用分块矩阵的主要原因。
5.7 初等矩阵
在数学中,大家都倾向于把一个复杂对象分解为若干个简单对象的组合。例如,在算术中,大于
等于 2 的整数可以分解为若干个素数的乘积。前面已经定义了矩阵的乘法,自然地会想到矩阵
是否也能进行类似的分解,即能否把一个复杂的矩阵分解为若干个比较简单的矩阵的乘积。
最简单的矩阵是零矩阵和单位矩阵。其次,比较简单的矩阵是如下定义的初等矩阵。
定义5.19 初等矩阵: 由单位矩阵 E 经过一次初等变换得到的矩阵称为初等矩阵。
与三种类型的初等变换相对应,有以下三种类型的初等矩阵。
P (i, j) =
1
.
.
.
1
0 ··· ··· ··· 1
.
.
. 1
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. 1
.
.
.
1 ··· ··· ··· 0
1
.
.
.
1
←− 第i行
←− 第j行
P (i(k)) =
1
.
.
.
1
k
1
.
.
.
1
←− 第i行
77

5.7 初等矩阵
P (i, j(k)) =
1
.
.
.
1 ··· k
.
.
.
.
.
.
1
.
.
.
1
←− 第i行
←− 第j行
利用矩阵乘法的定义,立即可以得到初等矩阵与矩阵初等变换的关系,即有如下引理:
引理 5.2
对一个 s × n 矩阵 A 作一初等行变换就相当于在 A 的左边乘上相应的 s × s 初等矩阵,
对 A 作一初等列变换就相当于在 A 的右边乘上相应的 n × n 的初等矩阵。
证明. 我们只看行变换的情形,列变换的情形可同样证明。令 B = (b
ij
) 为任意一个 s × s 矩阵,
A
1
, A
2
, ··· , A
s
为 A 的行向量。由矩阵的分块乘法,得
BA =
b
11
A
1
+ b
12
A
2
+ ··· + b
1s
A
s
b
21
A
1
+ b
22
A
2
+ ··· + b
2s
A
s
············
b
s1
A
1
+ b
s2
A
2
+ ··· + b
ss
A
s
分别令 B = P (i, j),B = P (i(k)),B = P (i, j(k)) 得
P (i, j)A =
A
1
.
.
.
A
j
.
.
.
A
i
.
.
.
A
s
P (i(k)) A =
A
1
.
.
.
kA
i
.
.
.
A
s
P (i, j(k)) A =
A
1
.
.
.
A
i
+ kA
j
.
.
.
A
j
.
.
.
A
s
这就相当于将 A 的第 i 行和第 j 行互换;相当于用 k 乘以 A 的第 i 行;相当于把 A 的第 j 行
的 k 倍加到第 i 行。
不难看出,初等矩阵都是可逆的,它们的逆矩阵还是初等矩阵。即:
P (i, j)
−1
= P (i, j)
P (i(k))
−1
= P (i(k
−1
))
P (i, j(k))
−1
= P (i, j(−k))
在行列式的计算或解线性方程组中,我们可以看到,用初等行变换可以化简矩阵。如果同时使用
行与列的初等变换,矩阵还可以进一步化简。又因为,初等变换是可逆的,所以我们可以引入如
下定义。
定义5.20 等价的矩阵: 矩阵 A 与矩阵 B 称为等价的,如果 B 可以由 A 经过一系列的初等变
换得到。
根据引理5.2以及上述矩阵等价的定义,对一矩阵作初等变换就相当于用相应的初等矩阵去乘这
个矩阵。因此,矩阵 A, B 等价的充分必要条件是有初等矩阵 P
1
, ··· , P
l
, Q
1
, ··· , Q
t
使
A = P
1
P
2
···P
l
BQ
1
Q
2
···Q
t
(5.2)
因为初等矩阵是可逆的,所以上式可以改写为:
78

5.7 初等矩阵
B = P
−1
1
P
−1
2
···P
−1
l
AQ
−1
1
Q
−1
2
···Q
−1
t
定理 5.9
任意一个 s × n 矩阵 A 都与一形式为
E
(r)
s×n
=
1 0 ··· 0 ··· 0
0 1 ··· 0 ··· 0
.
.
.
.
.
.
.
.
.
.
.
.
0 0 ··· 1 ··· 0
0 0 ··· 0 ··· 0
.
.
.
.
.
.
.
.
.
.
.
.
0 0 ··· 0 ··· 0
s×n
=
E
r×r
O
r×(n− r)
O
(s−r)× r
O
(s−r)× (n− r)
的矩阵等价,它称为矩阵 A 的标准形,主对角线上 1 的个数等于 A 的秩(1 的个数可以
为零)。
证明. 如果 A = O,那么它已经是标准形了。以下无妨假定 A 6= O。要证上述定理,只要证经
过初等变换,A 一定可以变成一左上角元素不为零的矩阵。
当 a
11
6= 0 时,把其余的行减去第一行的 a
−1
11
a
i1
(i = 2 , 3, ··· , s) 倍,其余的列减去第一列的
a
−1
11
a
1j
(j = 2, 3, ··· , n) 倍。然后,用 a
−1
11
乘第一行,A 就变成
1 0 ··· 0
0
.
.
. A
1
0
A
1
是一个 (s − 1) × (n − 1) 的矩阵。对 A
1
再重复以上的步骤,这样下去就可得出所要的标准
形。显然,标准形矩阵的秩就等于它主对角线上 1 的个数。而初等变换不改变矩阵的秩,所以 1
的个数也就是矩阵 A 的秩。
n 级可逆矩阵的秩为 n,所以由上述定理可知,可逆矩阵的标准形为单位矩阵;反之,若 n 级的
标准形为单位矩阵,它必然是可逆的。由5.2式即得
定理 5.10
n 级矩阵 A 为可逆的充分必要条件是它能表成一些初等矩阵的乘积:
A = Q
1
Q
2
···E ···Q
m
= Q
1
Q
2
···Q
m
(5.3)
上述定理表明,初等矩阵的乘积也是一个可逆矩阵,因此改写5.2式可得到以下推论。
推断 5.10-1 两个 s × n 矩阵 A, B 等价的充分必要条件为:存在可逆的 s 级矩阵 P 与可逆的
n 级矩阵 Q 使
A = P BQ
把5.3式改写一下,有
Q
−1
m
···Q
−1
2
Q
−1
1
A = E (5.4)
因为初等矩阵的逆矩阵还是初等矩阵,同时在矩阵 A 的左边乘初等矩阵就相当于对 A 作初等
行变换。因此,由5.4式可得
推断 5.10-2 可逆矩阵总可以经过一系列初等行变换化成单位矩阵。
以上的讨论提供了一个求逆矩阵的方法。设 A 是一 n 级可逆矩阵。由以上推论,有一系列初等
矩阵
P
1
,
···
,
P
m
使
P
m
···P
1
A = E (5.5)
79
第六章 线性空间
6.1 线性空间的定义
定义6.1 加法、数乘: 设 V 是一个非空集合,P 是一个数域,在集合 V 的元素之间定义两种代
数运算:
▷ 加法:定义一个法则,对于 V 中任意两个元素 α 和 β,在 V 中都有唯一的一个元素 γ 与
它们对应,记为 γ = α + β,γ 称为 α 和 β 的和。即加法是一个映射:V
×
V 7−→ V 。
▷ 数量乘法:定义一个法则,对于数域 P 中任意一个数 k 与 V 中的任意元素 α,在 V 中
都有唯一的一个元素 δ 与它们对应,称为 k 与 α 的数量乘积,记 δ = kα。即数乘是一个
映射:P
×
V 7−→ V 。
定义6.2 线性空间: 在 V 中定义加法和数量乘法(即定义6.1),并且加法、数量乘法满足以下 8
个条件,则称 V 是数域 P 上的线性空间,亦称为向量空间:
▷ 加法满足的四个规则
1. 加法结合律 ∀α, β, γ ∈ V ,有 (α + β) + γ = α + (β + γ)
2. 加法交换律 ∀α, β ∈ V , 有 α + β = β + α
3. 存在一个元素 0 ∈ V ,使得 ∀α ∈ V ,成立 , 0 + α = α,则 0 称为 V 的零元素
4. 存在负元,即 ∀α ∈ V ,存在 β ∈ V ,使得 α + β = 0
▷ 数量乘法满足的两个规则:
5. 1 律:1α = α
6. 数乘结合律 ∀k, l ∈ K, α ∈ V ,都有 k(lα) = (kl)α = l(kα)
▷ 加法与数量乘法共同满足两个规则:
7. 右分配律 ∀k, l ∈ K, α ∈ V ,都有 (k + l)α = kα + lα
8. 左分配律 ∀k ∈ K, α, β ∈ V ,都有 k(α + β) = kα + kβ
从逻辑上看,必须先有线性空间,才能定义线性变换,但从历史的发展来看,是先有线性变换,
后有现代数学所定义的线性空间。虽然在 17 世纪,当笛卡尔提出笛卡尔坐标系后,数学上就
出现了向量和向量空间的朴素概念,但现代向量空间的抽象定义在 1888 年才由意大利数学家
Giuseppe Peano 提出,而代表线性变换的矩阵乘法早在 1855 年就由英国数学家 Arthur Cayley
提出。
实际上,线性空间是为线性变换量身打造的。也就是说,对于一个域 F 和一个集合 S,如果可
以给 S 的元素定义加法运算和数量乘法运算,如果这两个运算符合线性空间的八条规则,且 S
对这两个运算封闭,那么我们就可以在 F 和 S 之上建立一个线性空间,在这个线性空间中执行
线性变换,且这些线性变换具有我们所期待的一切性质。
vector 一词来自拉丁语,最初的字面意思是 carrier(载体)。天文学家在 18 世纪首次使用它来
描述行星的运动。对他们来说,向量是将 A 点传送到 B 点的东西,它有特定的长度和方向。所
以在物理上,向量是一个有长度和方向的量。向量空间可以理解为是一个具有向量的空间,而这
个空间是容纳向量运动的载体,所谓的运动是指线性变换。
我还没见过有教材会讲述这八个规则的重要性,这可能会给学生留下一个印象:这八个规则是线
81

6.1 线性空间的定义
性空间与生俱来的,但数学从来没有什么与生俱来的规则。根据线性变换的定义,线性空间必须
要有向量加法,同时,向量加法应该满足一些基本的性质。这是合理的,倘若向量加法什么性质
都不满足,那么我们有了向量加法也做不了什么。此外,线性空间还必须要用数乘,当然数乘运
算也要满足一些基本性质,否则数乘运算并不能给我们带来什么用处。
向量加法需要满足结合律和交换律,这应该是容易理解的,若不满足两者,向量的加法运算就会
有很多麻烦,具体可参考第1.4节(运算律)。除此之外,在线性空间中,等量公理不能根据结合
律和交换律拓展到有 n(n ∈ N
∗
) 个元素参与运算的情况。
向量加法存在单位元和逆元这两个规则是有关联的,虽然存在单位元,并不一定有逆元,但存在
逆元则必定有单位元。逆元的定义需要借助单位元。试想一下,对于某个二元运算 ◦,如果不借
助单位元,我们可以如下定义元素 a 的逆元:
(a ◦ b) ◦ a
−1
= b
a
−1
◦ (a ◦ b) = b
如果 ◦ 满足结合律和交换律,则 a ◦a
−1
显然就是一个单位元。显然,以上定义逆元的方式难言
优雅,因此引入单位元的定义是有必要的。那为什么向量关于加法的逆元是重要的呢?这里不从
抽象层面的对称性进行考虑,只需要考虑一个基础且重要的概念——线性相关。
k
1
α
1
+ k
2
α
2
+ ··· + k
s
α
s
= 0
线性相关通过以上等式定义,若逆元不存在,上述等式显然是无法成立的。注意到,齐次线性方
程组是零向量的线性组合,所以此时,齐次线性方程组在线性空间中是不成立的,线性空间无法
使用齐次线性方程组的结论,我们也无法通过线性空间来研究齐次线性方程组。
现在,让我们思考一下,如果数乘不满足 1 律会发生什么。考虑如下简单的线性相关:
a
1
x
1
+ a
2
x
2
= 0
a
1
x
1
= −a
2
x
2
1
a
1
a
1
x
1
= −
a
2
a
1
x
2
1x
1
= −
a
2
a
1
x
2
若 1x
1
6= x
1
,那么当 a
1
x
1
+ a
2
x
2
= 0 成立时,x
1
= −
a
2
a
1
x
2
是不成立的。也就是说,线性相关
的两个定义会产生矛盾。因此,数乘的 1 律是有必要的。
如果数乘满足 1 律,但不满足结合律,这会产生矛盾。若 (kl)x 6= k(lx) ,令 l = 1 ,则有:
(k · 1)x 6= k(1x)
kx 6= kx
同样地,若数乘满足 1 律,且 k(α + β) 6= kα + kβ,令 k = 1,则有 α + β 6= α + β。
常见的线性空间有:
定义6.3 P: 数域 P 按照自身的加法和乘法,构成一个自身上的线性空间。
定义6.4 P
n
: 数域 P 中的 n 元向量构成数域 P 上的一个线性空间,记为 P
n
。
定义6.5 R
n
: n 维实向量的全体组成的集合为
R
n
=
{
x
= (
x
1
, x
2
,
···
, x
n
)
T
|
x
1
, x
2
,
···
, x
n
∈
R
}
R
n
叫做 n 维实向量空间。
定义6.6 P
m×n
: 元素属于数域 P 的 m ×n 矩阵,按矩阵的加法和数量乘法,构成数域 P 上的一
82

6.2 线性空间的简单性质
个线性空间,记为 P
m×n
。
定义6.7 P[x]
n
: 数域 P 上一元多项式环 P [x],满足上述 8 个规则,构成了一个数域 P 上的线
性空间。如果只考虑其中次数小于 n 的多项式,再添上零多项式也构成数域 P 上的一个线性空
间,用 P [x]
n
表示。
定义6.8 向量: 线性空间的元素称为向量(因此线性空间也称为向量空间)。即凡是符合线性空
间 8 条规则者,皆是向量。
在定义4.1中,向量被定义为一个有序数组,但这里给出了在抽象层面上向量的定义。n 维有序
数组是我们直观上所接触的向量,但这个有序数组背后可以代表任何事物,只要这些事物符合线
性空间的八条规则。因此,线性方程组的行系数或列系数也是向量,线性方程组可以表示为列向
量的线性组合。
定义6.9 矩阵: 二重复合向量称之为矩阵。
6.2 线性空间的简单性质
性质 1
零元素唯一。
证明. 设 0 与 0
′
均是零元素,则由零元素的性质(0 元的定义),有 0 = 0
′
+ 0 = 0
′
。
性质 2
任意元素的负元素唯一。
证明. ∀α ∈ V ,设 β, β
′
都是 α 的负向量,则 β = 0 + β = ( β
′
+ α) + β = β
′
+ (α + β) =
β
′
+ 0 = β
′
由于负向量唯一,我们用 −α 代表 α 的负向量,从而定义减法:
定义6.10 减法: α − β = α + (−β)
性质 3
1. 0α = 0
2. k0 = 0
3. (−1)α = −α
证明. 根据线性空间的 8 个性质:
证等式 1:
α + 0α = 1α + 0α = (1 + 0)α = 1α = α
即:α + 0α = α,等式两边加上 −α ,得到 0α = 0
证等式 3:
α + (−1)α = 1 α + (−1)α = (1 − 1)α = 0α = 0
即:α + (−1)α = 0 ,等式两边加上 −α,得到 (−1)α = −1α
证等式 2:
由数乘结合律
k00 = (k0)0 = k(00) = 0(k0)
83
6.3 向量加法交换律的
由等式 2 可知:00 = 0,则 k(00) = k0;设 β = k0,则 0β = 0
即:
k(00) = k0 = 0β = 0
性质 4
如果 kα = 0,那么 k = 0 或者 α = 0
证明. 假设:k 6= 0,则
1
k
(kα) =
1
k
0 = 0
由数乘结合律:
1
k
(kα) = (
1
k
k)α = α
则
1
k
(kα) = 0 = α
6.3 向量加法交换律的
6.4 维数、基、坐标
定义6.11 维数: 如果线性空间 V 有 n 个线性无关的向量,但是没有数目更多的线性无关的向
量,那么 V 就 n 维的。如果 V 存在无限多的线性无关的向量,则 V 就是无限维的。
定义6.12 基: 在 n 维线性空间 V 中,n 个线性无关的向量 ε
1
, ε
2
, ··· , ε
n
称为 V 的一组基。
线性空间 V 中的元素被称为向量,因此 V 相当于一个向量组,一组基即是 V 的一个极大
线性无关部分组,基的个数是该向量组的秩,也是该线性空间的维数。
根据推论4.1-2,由 n 维线性空间 V 的一组基 ε
1
, ε
2
, ··· , ε
n
和 V 中任一向量 a 组成的向量组必
是线性相关的,由命题4.5的证明过程可知,a 可由 ε
1
, ε
2
, ··· , ε
n
线性表出。因之,有如下定义。
定义6.13 坐标: V 中的任意元素都可以由 V 的一组基线性表出,例如 a ∈ V, a = a
1
ε
1
+ a
2
ε
2
+
··· + a
n
ε
n
,其中系数 a
1
, a
2
··· , a
n
称为 a 在基 ε
1
, ε
2
, ··· , ε
n
下的坐标,记为 (a
1
, a
2
, ··· , a
n
)。
由以上定义看来,在给出空间 V 的一组基之前, 必须先确定 V 的维数。实际上,这两个问题常
常是同时解决的。
定理 6.1
如果在线性空间 V 中有 n 个线性无关的向量 α
1
, α
2
, ··· , α
n
, 且 V 中任一向量都可以用
它们线性表出, 那么 V 是 n 维的, 而 α
1
, α
2
, ··· , α
n
就是 V 的一组基。
证明. 已有条件:
1. α
1
, α
2
, ··· , α
n
是 V 中 n 个线性无关的向量。
2. V 中任一向量都可以用 α
1
, α
2
, ··· , α
n
线性表出。
根据维度的定义,要证明 V 是 n 维的,也就是要证明 V 最多只能有 n 个线性无关的向量。因
为部分组线性相关,向量组必定线性相关,只需证 V 中任意 n + 1 个向量必定线性相关。
84

6.5 基变换与坐标变换
设 β
1
, β
2
, ··· , β
n+1
是 V 中任意 n + 1 个向量,它们可以用 α
1
, α
2
, ··· , α
n
线性表出。由定
理4.1或其推论可知,它们必定线性相关。假如它们线性无关, 就有 n + 1 ⩽ n, 于是得出矛盾。由
此可知,V 最多有 n 个线性无关的向量,因此 V 是 n 维的。
根据基的定义,α
1
, α
2
, ··· , α
n
是 V 中 n 个线性无关的向量,因此它们是 V 的一组基。
命题 6.1 在同一组基下,同一个元素的坐标是唯一的。
证明. 由定理4.2(线性表示的唯一性) 可证明。
6.5 基变换与坐标变换
设 ε
ε
ε
1
, ε
ε
ε
2
, ··· , ε
ε
ε
n
、ε
ε
ε
′
1
, ε
ε
ε
′
2
, ··· , ε
ε
ε
′
n
是 n 维线性空间 V 中的两组基,它们的关系是:
ε
′
1
= a
11
ε
1
+ a
21
ε
2
+ ··· + a
n1
ε
n
ε
′
2
= a
12
ε
1
+ a
22
ε
2
+ ··· + a
n2
ε
n
···
ε
′
n
= a
1n
ε
1
+ a
2n
ε
2
+ ··· + a
nn
ε
n
(6.1)
设向量 ξ 在这两组基下的坐标分别是 (x
1
, x
2
, ··· , x
n
) 和 (x
′
1
, x
′
2
, ··· , x
′
n
)。即:
ξ = x
1
ε
1
+ x
2
ε
2
+ ··· + x
n
ε
n
= x
′
1
ε
′
1
+ x
′
2
ε
′
2
+ ··· + x
′
n
ε
′
n
仿照矩阵乘法,上式可形式地记为如下:
ξ = (ε
1
, ε
2
, ··· , ε
n
)
x
1
x
2
.
.
.
x
n
= (ε
′
1
, ε
′
2
, ··· , ε
′
n
)
x
′
1
x
′
2
.
.
.
x
′
n
(6.2)
相仿地,公式6.1可以写为:
(ε
′
1
, ε
′
2
, ··· , ε
′
n
) = (ε
1
, ε
2
, ··· , ε
n
)
a
11
a
12
··· a
1n
a
21
a
22
··· a
2n
.
.
.
.
.
.
.
.
.
a
n1
a
n2
··· a
nn
(6.3)
将6.3式右端的矩阵记为 A,称 A 为由基 (ε
1
, ε
2
, ··· , ε
n
) 到 (ε
′
1
, ε
′
2
, ··· , ε
′
n
) 的过渡矩阵。
需要强调,这些写法是“形式的”。因为 ε
i
和 ε
′
i
是抽象层面的向量,并不是由数域 P 中的元
素组成的有序数组。由 (ε
′
1
, ε
′
2
, ··· , ε
′
n
) 的线性无关可知6.1式中系数矩阵是行满秩的,也就是说,
过渡矩阵 A 是可逆的。
在利用形式写法来作计算之前,我们首先要指出这种写法所具有的一些运算规律。
((α
1
, α
2
, ··· , α
n
) A) B = (α
1
, α
2
, ··· , α
n
) (AB)
(α
1
, α
2
, ··· , α
n
) A + (α
1
, α
2
, ··· , α
n
) B = (α
1
, α
2
, ··· , α
n
) (A + B)
(α
1
, α
2
, ··· , α
n
) A + (β
1
, β
2
, ··· , β
n
) A = (α
1
+ β
1
, α
2
+ β
2
, ··· , α
n
+ β
n
) A
(k) (α
1
, α
2
, ··· , α
n
) A = (α
1
, α
2
, ··· , α
n
) (kA) =k ((α
1
, α
2
, ··· , α
n
) A)
上述运算规律的证明与矩阵乘法满足结合律,左(右)分配律,以及矩阵乘法与数量乘法的关系
式证明一样,读者可以自行验证。
现在要做的就是找出 (x
1
, x
2
, ··· , x
n
) 与 (x
′
1
, x
′
2
, ··· , x
′
n
) 的关系。令
85

6.5 基变换与坐标变换
A =
a
11
a
12
··· a
1n
a
21
a
22
··· a
2n
.
.
.
.
.
.
.
.
.
a
n1
a
n2
··· a
nn
x =
x
1
x
2
.
.
.
x
n
x
′
=
x
′
1
x
′
2
.
.
.
x
′
n
将式6.3代入式6.2,得到
ξ = (ε
1
, ε
2
, ··· , ε
n
)x = ((ε
1
, ε
2
, ··· , ε
n
)A) x
′
= (ε
1
, ε
2
, ··· , ε
n
)
Ax
′
(6.4)
可得 x = Ax
′
,即:
x
1
x
2
.
.
.
x
n
=
a
11
a
12
··· a
1n
a
21
a
22
···
a
2n
.
.
.
.
.
.
.
.
.
a
n1
a
n2
··· a
nn
x
′
1
x
′
2
.
.
.
x
′
n
(6.5)
或者
x
′
1
x
′
2
.
.
.
x
′
n
=
a
11
a
12
··· a
1n
a
21
a
22
··· a
2n
.
.
.
.
.
.
.
.
.
a
n1
a
n2
··· a
nn
−1
x
1
x
2
.
.
.
x
n
(6.6)
6.5.1 基变换解释
上一节的叙述已经尽量简单,这里用一个直观、简单的例子再解释一遍。
如果在二维空间有一个向量,当选定一个坐标系之后,我们就有一种用坐标表示它的标准
1
方法。
坐标系只是一个框架,提供了一种将空间向量可视化的途径,它依赖于我们对基的选择,空间中
本没有坐标系。很自然的问题就是,我们如何在不同的坐标系之间进行转化。例如:
相对于当前坐标系(二维空间),基向量总是
1 0
0 1
。设当前的坐标系为 xOy,那么它的基就是
1 0
0 1
。现在出现了一个新的坐标系 x
′
Oy
′
,那么,我们要把新坐标系的基用当前的基表示。假
设新坐标系的基被表示为
2 −1
1 1
。然后在新坐标系下有一个向量
x
y
,在原坐标系有一个线
性变换
1 −1
3 2
。
x
y
在原坐标系的描述 =
2 −1
1 1
x
y
x
y
在原坐标系的线性变换 =
1 −1
3 2
2 −1
1 1
x
y
x
y
在新坐标系的线性变换 =
2 −1
1 1
−1
1 −1
3 2
2 −1
1 1
x
y
= 基变换的逆变 * 线性变换 * 基变换
基变换的逆变 × 线性变换 × 基变换,这三个矩阵的复合给出的就是新坐标系描述的线性变换矩
阵。
1
所谓的标准指的是这种坐标表示是唯一的。
86
6.6 线性子空间
6.6 线性子空间
定义6.14 线性子空间: 数域 P 上线性空间 V 的一个非空子集合 W 称为 V 的一个线性子空间
(或简称子空间),如果 W 对于 V 的加法和数乘运算也构成数域 P 上的线性空间。
定理 6.2
如果域 P 上的线性空间 V 的非空子集合 W 对于 V 的加法和数乘运算是封闭的,也就
是满足以下条件,那么 W 是一个子空间。
1. 如果 W 中包含向量 α,那么 W 同时包含域 P 中的数 k 与 α 的数量乘积 kα。
2. 如果 W 中包含向量 α 与 β,那么 W 就同时包含 α 与 β 的和 α + β。
证明. 要证明 W 也是一个线性空间,就是要证明 W 符合线性空间定义的 8 个条件。
因为 W 是 V 的子集,所以 W 的加法和数乘运算符合线性空间定义中的 1、2、5、6、7、8 条
件是显然的。因此,只需要证明 W 的加法和数乘运算具有封闭性,以及对于加法运算,W 中存
在零元且所有元素皆存在负元即可。
由定理中给出的两个条件,显然 W 的加法和数乘运算具有封闭性。利用第一个条件,当 k = 0
时,可得 W 存在零元,当 k = −1 时,可得 W 中所有元素皆存在负元。
注意,线性空间 V 和它的子空间 W 都是在同一个数域 P 上的。显然,线性空间 V 本身也是
V 的一个子空间。既然线性子空间本身也是一个线性空间,线性空间中的概念(如维数、基、坐
标等)当然也可以应用到线性子空间上。因为在线性子空间中不可能比在整个空间中有更多数
目的线性无关的向量。所以,任何一个线性子空间的维数不能超过整个空间的维数。
定义6.15 零子空间: 在线性空间中,由单个的零向量所组成的子集合是一个线性子空间,它叫
做零子空间。
定义6.16 平凡子空间: 在线性空间中,零子空间和线性空间本身这两个子空间有时候叫做平凡
子空间,而其他的线性子空间叫做非平凡子空间。
定义6.17 生成的子空间: 设 α
1
, α
2
, ··· , α
r
是线性空间 V 中一组向量,不难看出,这组向量所
有可能的线性组合
k
1
α
1
+ k
2
α
2
+ ··· + k
r
α
r
所成的集合是非空的,而且对两种运算封闭(易证),因而是 V 的一个子空间,这个子空间叫做
由 α
1
, α
2
, ··· , α
r
生成的子空间,记为 L (α
1
, α
2
, ··· , α
r
)。
由子空间的定义可知,如果 V 的一个子空间包含向量 α
1
, α
2
, ···, α
r
,那么就一定包含它们所
有的线性组合,也就是说,一定包含 L (α
1
, α
2
, ··· , α
r
) 作为子空间,否则 V 对 α
1
, α
2
, ···, α
r
的向量加法和数乘运算就不是封闭的。
在有限维线性空间中 V ,任何一个子空间都可以这样得到。事实上,设 W 是 V 的一个子空间,
W 当然也是有限维的。设 α
1
, α
2
, ··· , α
r
是 W 的一组基,就有 W = L (α
1
, α
2
, ··· , α
r
)。
定理 6.3
1. 两个向量组生成相同子空间的充分必要条件是这两个向量组等价。
2. L (α
1
, α
2
, ··· , α
r
) 的维数等于向量组 α
1
, α
2
, ··· , α
r
的秩。
证明. (1) 设 α
1
, α
2
, ··· , α
r
与 β
1
, β
2
, ··· , β
s
是两个向量组。先证命题 1 的必要性。如果
L (α
1
, α
2
, ··· , α
r
) = L (β
1
, β
2
, ··· , β
s
)
那么每个向量 α
i
(i = 1, 2, ··· , r) 作为 L(β
1
, β
2
, ··· , β
s
) 中的向量都可以被 β
1
, β
2
, ··· , β
s
线
性表出。同样地,每个向量 β
j
(j = 1, 2, ··· , s) 作为 L(α
1
, α
2
, ··· , α
r
) 中的向量也都可以被
α
1
, α
2
, ··· , α
r
线性表出,因而这两个向量组等价。
87

6.7 子空间的交与和
再证命题 1 的充分性。如果这两个向量组等价,那么凡是可以被 α
1
, α
2
, ··· , α
r
线性表出的向量
都可以被 β
1
, β
2
, ··· , β
s
线性表出,反过来也一样,因而 L (α
1
, α
2
, ··· , α
r
) = L (β
1
, β
2
, ··· , β
s
)。
(2) 设向量组 α
1
, α
2
, ··· , α
r
的秩是 s, 而 α
1
, α
2
, ··· , α
s
(s ⩽ r) 是它的一个极大线性无关组。
因为 α
1
, α
2
, ··· , α
r
与 α
1
, α
2
, ··· , α
s
等价,所以 L
(
α
1
, α
2
, ··· , α
r
) = L
(
α
1
, α
2
, ··· , α
s
)。由
定理6.1,α
1
, α
2
, ··· , α
s
就是 L (α
1
, α
2
, ··· , α
r
) 的一组基,因而 L (α
1
, α
2
, ··· , α
r
) 的维数就
是 s。
定理 6.4
设 W 是数域 P 上 n 维线性空间 V 的一个 m 维子空间,α
1
, α
2
, ··· , α
m
是 W 的一组
基,那么这组向量必定可扩充为整个空间的基。也就是说, 在 V 中必定可以找到 n − m
个向量 α
m+1
, α
m+2
, ··· , α
n
,使得 α
1
, α
2
, ··· , α
n
是 V 的一组基。
证明. 对维数差 n − m 作归纳法。
当 n −m = 0,定理显然成立,因为 α
1
, α
2
, ··· , α
m
已经是 V 的基。现在假定 n −m = k 时定
理成立,我们考虑 n − m = k + 1 的情形。
既然 α
1
, α
2
, ··· , α
m
还不是 V 的一组基,它又是线性无关的,那么在 V 中必定有一个向量
α
m+1
不能被 α
1
, α
2
, ··· , α
m
线性表出,把 α
m+1
添加进去,容易证明,α
1
, α
2
, ··· , α
m
, α
m+1
必定是线性无关的。
由定理6.3,子空间 L (α
1
, α
2
, ··· , α
m
, α
m+1
) 是 m + 1 维的。因为 n −(m + 1) = (n −m) −1 =
k + 1 − 1 = k, 由归纳法假设, L (α
1
, α
2
, ··· , α
m
, α
m
+1
) 的基 α
1
, α
2
, ··· , α
m
, α
m
+1
可以扩充
为整个空间的基。
6.7 子空间的交与和
定理 6.5
如果 V
1
, V
2
是线性空间 V 的两个子空间,那么它们的交 V
1
T
V
2
也是 V 的子空间。
证明. 要证明 V
1
T
V
2
是线性子空间,只需证明 V
1
T
V
2
存在零元、负元,且对加法和数乘封闭
即可。
因为 0 ∈ V
1
, 0 ∈ V
2
,可知 0 ∈ V
1
T
V
2
, 因而 V
1
T
V
2
是非空的。
对于 ∀α ∈ V
1
T
V
2
,则有 α ∈ V
1
且 α ∈ V
2
,因此,−α ∈ V
1
且 −α ∈ V
2
,所以 −α ∈ V
1
T
V
2
。
对于 V
1
T
V
2
中的任意两个向量 α, β,必有 α, β ∈ V
1
,且 α, β ∈ V
2
,那么 α+β ∈ V
1
, α+β ∈ V
2
,
因此 α + β ∈ V
1
T
V
2
。
对数量乘积可以同样地证明。所以 V
1
T
V
2
是 V 的子空间。
由集合的交的定义可以看出,子空间的交适合下列运算规:
1. 交换律:V
1
T
V
2
= V
2
T
V
1
2. 结合律:(V
1
T
V
2
)
T
V
3
= V
1
T
(V
2
T
V
3
)
由结合律,我们可以定义多个子空间的交
V
1
\
V
2
\
···
\
V
s
=
s
\
i=1
V
i
它也是子空间。
定义6.18 子空间的和: 设 V
1
, V
2
是线性空间 V 的子空间,所谓 V
1
与 V
2
的和,是指由所有能
表示成 α
1
+ α
2
,而 α
1
∈ V
1
, α
2
∈ V
2
的向量组成的子集合,记作 V
1
+ V
2
。
88

6.7 子空间的交与和
定理 6.6
如果 V
1
, V
2
是线性空间 V 的子空间,那么它们的和记作 V
1
+ V
2
也是 V 的子空间。
证明. 首先,V
1
+ V
2
显然是非空的。其次,对于 V
1
+ V
2
中的任意两个元素 α 和 β,不妨设
α = α
1
+ α
2
, α
1
∈ V
1
, α
2
∈ V
2
β = β
1
+ β
2
, β
1
∈ V
1
, β
2
∈ V
2
那么
α + β = (α
1
+ β
1
) + (α
2
+ β
2
) .
又因 V
1
, V
2
是子空间,故有
α
1
+ β
1
∈ V
1
, α
2
+ β
2
∈ V
2
因此
α + β ∈ V
1
+ V
2
同样可证,kα = kα
1
+ kα
2
∈ V
1
+ V
2
。
令 k = 0 和 k = −1,即可证明零元和所有元素的负元都在 V
1
+ V
2
中。
由定义不难看出,子空间的和适合下列运算规律:
V
1
+ V
2
= V
2
+ V
1
(交换律)
(V
1
+ V
2
) + V
3
= V
1
+ (V
2
+ V
3
) (结合律)
由结合律,我们可以定义多个子空间的和
V
1
+ V
2
+ ··· + V
s
=
s
X
i=1
V
i
.
它是由所有表示成
α
1
+ α
2
+ ··· + α
s
, α
i
∈ V
i
(i = 1, 2, ··· , s)
的向量组成的子空间。
不难证明,关于子空间的交与和有以下结论:
1. 设 V
1
, V
2
, W 都是子空间,那么由 W ⊂ V
1
与 W ⊂ V
2
可推出 W ⊂ V
1
∩V
2
;而由 W ⊃ V
1
与 W ⊃ V
2
可推出 W ⊃ V
1
+ V
2
。
2. 对于子空间 V
1
与 V
2
,以下三个论断是等价的:
1) V
1
⊂ V
2
2) V
1
∩ V
2
= V
1
3) V
1
+ V
2
= V
2
这些结论的证明留给读者。
定理 6.7. 维数公式
如果 V
1
, V
2
是线性空间 V 的子空间,那么
维 (V
1
) + 维 (V
2
) = 维 (V
1
+ V
2
) + 维
V
1
\
V
2
证明. 设 V
1
, V
2
的维数分别是 n
1
, n
2
, V
1
∩ V
2
的维数是 m。取 V
1
∩ V
2
的一组基
89

6.7 子空间的交与和
α
1
, α
2
, ··· , α
m
如果 m = 0, 这个基是空集, 下面的讨论中 α
1
, ··· , α
m
不出现,但讨论同样能进行。由定理6.4,
它可以扩充成 V
1
的一组基
α
1
, α
2
, ··· , α
m
, β
1
, ··· , β
n
1
−m
也可以扩充成 V
2
的一组基
α
1
, α
2
, ··· , α
m
, γ
1
, ··· , γ
n
2
−m
如果能证明,向量组
α
1
, α
2
, ··· , α
m
, β
1
, ··· , β
n
1
−m
, γ
1
, ··· , γ
n
2
−m
(1)
是 V
1
+ V
2
的一组基。这样,V
1
+ V
2
的维数就等于 n
1
+ n
2
− m,因而维数公式成立。
因为
V
1
= L (α
1
, ··· , α
m
, β
1
, ··· , β
n
1
−m
)
V
2
= L (α
1
, ··· , α
m
, γ
1
, ··· , γ
n
2
−m
)
所以
V
1
+ V
2
= L (α
1
, ··· , α
m
, β
1
, ··· , β
n
1
−m
, γ
1
, ··· , γ
n
2
−m
)
要证向量组 (1) 是 V
1
+ V
2
的一组基,现在只需要再证明向量组 (1) 是线性无关的。即证明以下
等式中,所有向量的系数只能全为 0。
k
1
α
1
+ ··· + k
m
α
m
+ p
1
β
1
+ ··· + p
n
1
−m
β
n
1
−m
+ q
1
γ
1
+ ··· + q
n
2
−m
γ
n
2
−m
= 0
令
α = k
1
α
1
+ ··· + k
m
α
m
+ p
1
β
1
+ ··· + p
n
1
−m
β
n
1
−m
(2)
= −q
1
γ
1
− ··· − q
n
2
−m
γ
n
2
−m
(3)
由等式 (2) 可知,α ∈ V
1
;而由等式 (3) 看出,α ∈ V
2
。于是,α ∈ V
1
∩ V
2
,所以 α 可以被
α
1
, α
2
, ··· , α
m
线性表示。令
α = l
1
α
1
+ l
2
α
2
+ ··· + l
m
α
m
(4)
由等式 (3) 和等式 (4) 可得
l
1
α
1
+ ··· + l
m
α
m
+ q
1
γ
1
+ ··· + q
n
2
−m
γ
n
2
−m
= 0
由于 α
1
, ··· , α
m
, γ
1
, ··· , γ
n
2
−m
线性无关,得 l
1
= ··· = l
m
= q
1
= ··· = q
n
2
−m
= 0,因而
α = 0。从而有 k
1
α
1
+ ··· + k
m
α
m
+ p
1
β
1
+ ··· + p
n
1
−m
β
n
1
−m
= 0。
由于 α
1
, ··· , α
m
, β
1
, ··· , β
n
1
−m
线性无关,又得
k
1
= ··· = k
m
= p
1
= ··· = p
n
1
−m
= 0
这就证明了 α
1
, ··· , α
m
, β
1
, ··· , β
n
1
−m
, γ
1
, ··· , γ
n
2
−m
线性无关,因而它是 V
1
+ V
2
的一组基,
故维数公式成立。
从维数公式可以看到,和的维数往往要比维数的和来得小。例如,在三维几何空间中,两张通过
原点的不同的平面之和是整个三维空间,而其维数之和却等于 4。由此说明这两张平面的交是一
维的直线。
推断 6.7-1 如果 n 维线性空间 V 中两个子空间 V
1
, V
2
的维数之和大于 n,那么 V
1
, V
2
必含有
90

6.8 子空间的直和
非零的公共向量。
证明. 因为
维 (V
1
+ V
2
) + 维 (V
1
∩ V
2
) = 维 (V
1
) + 维 (V
2
) > n
又因为 V
1
+ V
2
是 V 的子空间而有
维 (V
1
+ V
2
) ⩽ n
所以
维 (V
1
∩ V
2
) > 0
这就是说,V
1
∩ V
2
中含有非零向量。
6.8 子空间的直和
子空间的直和是子空间的和的一个重要的特殊情形。
定义6.19 直和: 设 V
1
, V
2
是线性空间 V 的子空间, 如果和 V
1
+ V
2
中每个向量 α 的分解式
α = α
1
+ α
2
, α
1
∈ V
1
, α
2
∈ V
2
是唯一的,这个和就称为直和,记为 V
1
⊕ V
2
。
定理 6.8
和 V
1
+ V
2
是直和的充分必要条件是等式
α
1
+ α
2
= 0, α
i
∈ V
i
(i = 1, 2)
只有在 α
i
全为零向量时才成立。
证明. 定理的条件实际上就是:零向量的分解式是唯一的。根据直和的定义,这个条件显然是必
要的。下面来证这个条件的充分性。假设 α ∈ V
1
+ V
2
,它有两个分解式
α = α
1
+ α
2
= β
1
+ β
2
α
i
, β
i
∈ V
i
(i = 1, 2)
于是
(α
1
− β
1
) + (α
2
− β
2
) = 0
其中 α
i
− β
i
∈ V
i
(i = 1, 2)。由定理的条件,应有
α
i
− β
i
= 0, α
i
= β
i
(i = 1, 2)
这就是说, 向量 α 的分解式是唯一的。
推断 6.8-1 和 V
1
+ V
2
为直和的充分必要条件是
V
1
∩ V
2
= {0}
证明. 利用上述定理,先证条件的充分性,即证零向量的分解式是唯一的。假设有等式
α
1
+ α
2
= 0, α
i
∈ V
i
(i = 1, 2)
那么 α
1
和 −α
2
互为逆元,它们必定时存在 V
1
和 V
2
之中,即
α
1
= −α
2
∈ V
1
∩ V
2
由假设 V
1
∩ V
2
= {0},所以
91

6.8 子空间的直和
α
1
= α
2
= 0
这就证明了 V
1
+ V
2
是直和。
再证必要性。任取向量 α ∈ V
1
∩ V
2
,于是零向量可以表成
0 = α + (−α), α ∈ V
1
, −α ∈ V
2
因为是直和,零向量的分解式必定唯一,且分解式 0 = 0 + 0 必定存在,所以 α = −α = 0。这
就证明了 V
1
∩ V
2
= {0}。
定理 6.9
设 V
1
, V
2
是 V 的子空间, 令 W = V
1
+ V
2
, 则
W = V
1
⊕ V
2
的充分必要条件为维 (W ) = 维 (V
1
) + 维 ( V
2
)。
证明. 因为
维(W ) + 维
(
V
1
∩ V
2
) = 维
(
V
1
) + 维
(
V
2
)
由前面的推论知 V
1
+ V
2
为直和的充要条件是 V
1
∩ V
2
= {0},这是与维 (V
1
∩ V
2
) = 0 等价的,
也就与维 (W ) = 维 (V
1
) + 维 (V
2
) 等价。这就证明了定理。
定理 6.10
设 U 是线性空间 V 的一个子空间,那么一定存在一个子空间 W 使 V = U ⊕ W 。
证明. 取 U 的一组基 α
1
, ··· , α
m
。把它扩充为 V 的一组基 α
1
, ··· , α
m
, α
m+1
, ··· , α
n
。令
W = L (α
m+1
, ··· , α
n
)
W 即满足要求。
子空间的直和的概念可以推广到多个子空间的情形。
定义6.20 多个子空间的直和: 设 V
1
, V
2
, ··· , V
s
都是线性空间 V 的子空间。如果和 V
1
+ V
2
+
··· + V
s
中每个向量 α 的分解式
α = α
1
+ α
2
+ ··· + α
s
, α
i
∈ V
i
(i = 1, 2, ··· , s)
是唯一的, 这个和就称为直和, 记为 V
1
⊕ V
2
⊕ ··· ⊕ V
s
。
和两个子空间的直和一样, 我们有
定理 6.11
V
1
, V
2
, ··· , V
s
是 V 的一些子空间,下面这些条件是等价的:
1. W =
P
V
i
是直和
2. 零向量的表法唯一
3. V
i
TP
j̸=i
V
j
= {0} (i = 1, 2, ··· , s)
4. 维(W ) = Σ维 (V
i
)
这个定理的证明和 s = 2 的情形基本一样,这里就不再重复了。
92

6.9 线性空间的同构
6.9 线性空间的同构
设 ε
1
, ε
2
, ··· , ε
n
是线性空间 V 的一组基,在这组基下,V 中每个向量都有确定的坐标,而向
量的坐标可以看成 P
n
的元素。因此,向量与它的坐标之间的对应实质上就是 V 到 P
n
的一个
映射。即 V 中向量在 P
n
中的像为它在基 ε
1
, ε
2
, ··· , ε
n
下的坐标。显然,这个映射是单射与满
射,换句话说,坐标给出了线性空间 V 与 P
n
的一个双射。这个对应的重要性表现在它与运算
的关系上。设
α = a
1
ε
1
+ a
2
ε
2
+ ··· + a
n
ε
n
β = b
1
ε
1
+ b
2
ε
2
+ ··· + b
n
ε
n
即向量 α, β 的坐标分别是 (a
1
, a
2
, ··· , a
n
) , (b
1
, b
2
, ··· , b
n
),那么
α + β = (a
1
+ b
1
) ε
1
+ (a
2
+ b
2
) ε
2
+ ··· + (a
n
+ b
n
) ε
n
kα = ka
1
ε
1
+ ka
2
ε
2
+ ··· + ka
n
ε
n
于是向量 α + β, kα 的坐标分别是
(a
1
+ b
1
, a
2
+ b
2
, ··· , a
n
+ b
n
) = (a
1
, a
2
, ··· , a
n
) + (b
1
, b
2
, ··· , b
n
)
(ka
1
, ka
2
, ··· , ka
n
) = k (a
1
, a
2
, ··· , a
n
)
以上的式子说明在向量用坐标表示之后,它们的运算就可以归结为它们坐标的运算,而坐标的运
算规则取决于域 P 。因而线性空间 V 的讨论也就可以归结为 P
n
的讨论。为了确切地说明这一
点,先引入下列定义。
定义6.21 同构的线性空间、同构映射: 数域 P 上两个线性空间 V 与 V
′
称为同构的,如果由 V
到 V
′
有一个双射 σ,具有以下性质:
1. σ(α + β) = σ(α) + σ(β)
2. σ(kα) = kσ(α)
其中 α, β 是 V 中任意向量,k 是 P 中任意数。这样的映射 σ 称为同构映射,或简称为同构。
注意,线性空间之间的同构映射本质上是可逆的,且保持结构(向量加法和数乘)的映射。同构
映射是线性映射,但线性映射不一定是同构映射,因为线性映射不一定是可逆的,例如零变换
O。
由定义可以看出,同构映射σ具有下列基本性质:
性质 1
(i) σ(0) = 0
(ii) σ(−α) = −σ(α)
证明. 根据同构的性质,可知 σ(kα) = kσ(α)。令 k = 0,可得 σ(0α) = 0σ(α)。由线性空间的
性质,有 0α = 0, 0σ(α) = 0,因此 σ(0) = 0。
令 k = −1,有 σ(−1α) = −1σ(α)。由线性空间的性质,有 −1α = −α, −1σ(α) = −σ(α),因
此 σ(−α) = −σ(α)。
性质 2
同构保持线性组合的关系,即:
σ (k
1
α
1
+ k
2
α
2
+ ··· + k
r
α
r
) = k
1
σ (α
1
) + k
2
σ (α
2
) + ··· + k
r
σ (α
r
)
证明. 根据同构定义6.21中的 2 个性质可得(不要求向量加法的结合律)。
93
6.9 线性空间的同构
由性质 2 以及 σ(0) = 0,马上可得出:同构将线性相关的向量组映射为线性相关的向量组。这
个命题可等价地叙述为性质 3。
性质 3
V 中向量组 α
1
, α
2
, ··· , α
r
线性相关的充要条件是:它们的像 σ (α
1
) , σ (α
2
) , ··· , σ (α
r
)
线性相关。
证明. 先证必要性。假设有不全为零的一组数 k
1
, k
2
, ··· , k
r
使得下式成立:
k
1
α
1
+ k
2
α
2
+ ··· + k
r
α
r
= 0
根据性质 2 可得
k
1
σ (α
1
) + k
2
σ (α
2
) + ··· + k
r
σ (α
r
) = 0
再证充分性。由
k
1
σ (α
1
) + k
2
σ (α
2
) + ··· + k
r
σ (α
r
) = 0
有
σ (k
1
α
1
+ k
2
α
2
+ ··· + k
r
α
r
) = 0
因为 σ 是双射,所以只有 σ(0) = 0,即得
k
1
α
1
+ k
2
α
2
+ ··· + k
r
α
r
= 0
性质 4
同构保持向量组线性无关的关系。
证明. 设 σ 是 V 到 W 的同构,其中 V 是 n 维线性空间。α
1
, α
2
, ··· , α
s
(s ≤ n) 是 V 中任一
线性无关的向量组,即要使得下式成立
k
1
α
1
+ k
2
α
2
+ ··· + k
s
α
s
= 0 (1)
k
1
, k
2
,
···
, k
s
只能全为
0
。由性质
2
可知,由
(1)
式可得,当
k
1
=
k
2
=
···
=
k
s
= 0
时,下式
成立
k
1
σ(α
1
) + k
2
σ(α
2
) + ··· + k
s
σ(α
s
) = 0 (2)
要证明 σ(α
1
), σ(α
2
), ··· , σ(α
s
) 线性无关,只需要证明只有 k
1
, k
2
, ··· , k
s
全为 0 时,(2) 式才
成立。对 (2) 式应用 σ 的逆映射 σ
−1
可得到 (1) 式
0 = k
1
σ
−1
σ(α
1
) + k
2
σ
−1
σ(α
2
) + ··· + k
s
σ
−1
σ(α
s
)
= k
1
α
1
+ k
2
α
2
+ ··· + k
s
α
s
假设有一组不全为 0 的数 k
1
, k
2
, ··· , k
s
能使得 (2) 式成立,那么这组不全为 0 的数同样也能使
得 (1) 式成立。这与向量组 α
1
, α
2
, ··· , α
s
是线性无关的矛盾。因此,σ(α
1
), σ(α
2
), ··· , σ(α
s
)
线性无关。
由性质 4 可直接得到推论:同构将极大线性无关组映射为极大线性无关组。因为线性空间的一
组基是一个极大线性无关组,所以该推论可等价叙述为:若线性映射 σ : V 7−→ W 是同构,则
线性空间 V 和 W 具有相同的维数。由此,可得到性质 5
94
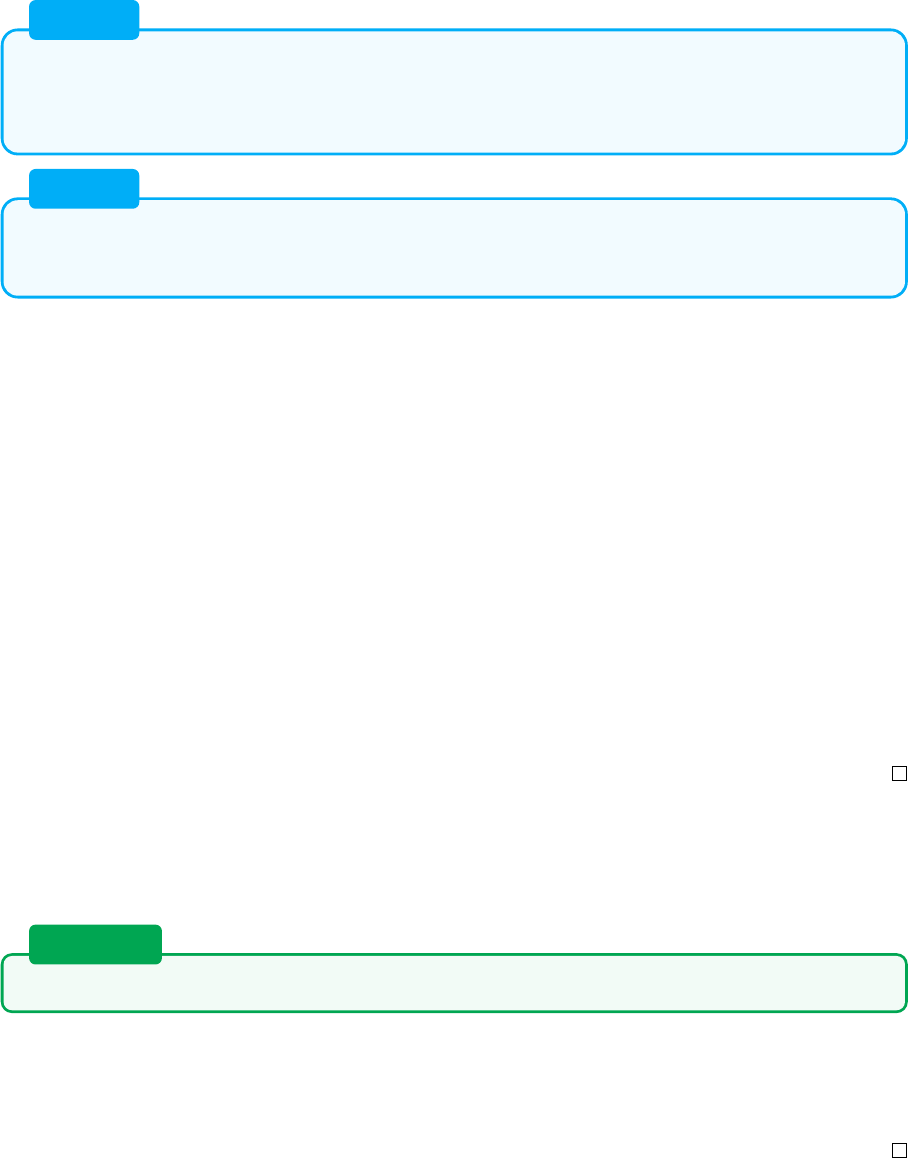
6.9 线性空间的同构
性质 5
如果 V
1
是 V 的一个线性子空间,那么,V
1
在 σ 下的像集合
σ (V
1
) = {σ(α) | α ∈ V
1
}
是 σ(V ) 的子空间,并且 V
1
与 σ (V
1
) 维数相同。
性质 6
(i) 同构映射的逆映射是同构映射。
(ii) 两个同构映射的乘积是同构映射。
证明. 设 σ 是线性空间 V 到 V
′
的同构映射,显然逆映射 σ
−1
是 V
′
到 V 的一个双射。我们来
证 σ
−1
还适合同构映射定义的两个条件。令 α
′
, β
′
是 V
′
中任意两个向量,于是
σσ
−1
α
′
+ β
′
= α
′
+ β
′
= σσ
−1
α
′
+ σσ
−1
β
′
= σ
σ
−1
α
′
+ σ
−1
β
′
两边用 σ
−1
作用,即得
σ
−1
α
′
+ β
′
= σ
−1
α
′
+ σ
−1
β
′
条件 2 可以同样地证明。
再设
σ
和
τ
分别是线性空间
V
到
V
′
和
V
′
到
V
′′
的同构映射,我们来证乘积
τσ
是
V
到
V
′′
的一个同构映射。显然,τσ 是单射与满射。由
τσ(α + β) = τ (σ( α ) + σ(β)) = τ σ(α) + τσ(β),
τσ(kα) = τ (kσ(α)) = kτ σ(α)
因此,τσ 是双射,且适合定义同构映射的 2 个条件,因而是同构映射。
任一线性空间 V 到自身的恒等映射显然是一同构映射,即同构具有自反性。又因为性质 6 表明,
同构具有对称性与传递性。因此,同构是线性空间之间的一种等价关系。既然数域 P 上任意一
个 n 维线性空间都与 P
n
同构,由同构的对称性与传递性即得,数域 P 上任意两个 n 维线性空
间都同构。综上所述, 我们有:
定理 6.12
数域 P 上两个有限维线性空间同构的充分必要条件是它们具有相同的维数。
证明. 假设 V
1
和 V
2
是数域 P 上的有限维线性空间,它们的维数分别为 n
1
和 n
2
。由上面的叙
述可知,V
1
和 V
2
分别与 P
n
1
和 P
n
2
同构。
先证充分性。若
n
1
=
n
2
=
n
,则
V
1
和
V
2
都与
P
n
同构,由同构的传递性可知,
V
1
和
V
2
同构。
由同构的性质 4 或性质 5 可得到必要性。
当我们在抽象的层面讨论线性空间时,我们并没有考虑线性空间的元素是什么,也没有考虑其
中运算是怎样定义的,而只涉及线性空间在所定义的运算下的代数性质。从这个观点看来,同构
的线性空间是可以不加区别的。因之,定理6.12说明了,维数是有限维线性空间的唯一的本质特
征。
特别地,每一个数域 P 上 n 维线性空间都与 n 元数组所成的空间 P
n
同构,而同构的空间有相
同的性质。由此可知,我们以前所得到的关于 n 元数组的一些结论,在一般的线性空间中也是
成立的,而不必要一一重新证明。
95
6.9 线性空间的同构
96
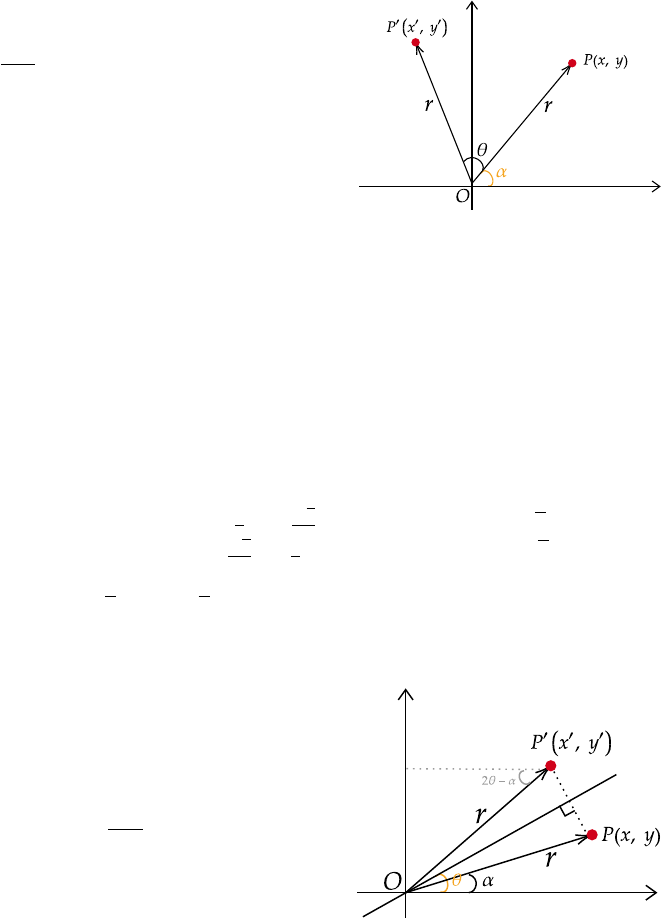
第七章 线性变换
7.1 平面上基本的线性变换
对线性代数较为熟悉的人都知道线性变换是线性代数的核心。有的线代教材会以线性变换作为
起点,但数学是一种人类活动的结果,线性变换并不是一开始便是如此形态。在深入了解线性变
换之前,我们先来看一下四种最简单的(线性)变换——平面上的旋转、镜射、伸缩和推移。
7.1.1 旋转变换
如图7.1,坐标平面上,OP = r ,且点 P (x, y) 满足
图 7.1: Rotation
x = r cos α
y = r sin α
那么,以原点 O 为中心,将点 P 依逆时针方向旋转 θ 角
后得点 P
′
(x
′
, y
′
) 。
x
′
= r cos(α + θ)
y
′
= r sin(α + θ)
⇒
x
′
= r(cos α cos θ − sin α sin θ) = x cos θ − y sin θ
y
′
= r(sin α cos θ + cos α sin θ) = x sin θ + y cos θ
若以矩阵表示,
x
′
y
′
=
cos θ −sin θ
sin θ cos θ
x
y
。因此,以原点 O 为中心逆时针方向旋转 θ 角
的线性变换的表示矩阵为
cos θ −sin θ
sin θ cos θ
, 并且将
cos θ −sin θ
sin θ cos θ
称为旋转矩阵。
例如,将点 A(2, −4) 以 O 为中心逆时针旋转 60
◦
,则
cos 60
◦
−sin 60
◦
sin 60
◦
cos 60
◦
2
−4
=
"
1
2
−
√
3
2
√
3
2
1
2
#
2
−4
=
1 + 2
√
3
−2 +
√
3
因此
,
对应点
A
′
的坐标为
(1 + 2
√
3
,
−
2 +
√
3)
。
7.1.2 镜射变换
图 7.2: Reection
若给定直线 L 是过原点且与 x 轴正向夹角为 θ 的直线,
考虑点 P (x, y) 对直线 L 的对称点为 P
′
(x
′
, y
′
) (如图7.2)。
那么,这种由 P 对应到 P
′
的变换称为对直线 L 的镜射,
且直线 L 被称为镜射轴。同样,令 OP = r ,且点 P (x, y)
满足
x = r cos α
y = r sin α
点 P
′
(x
′
, y
′
) 可表示为
97
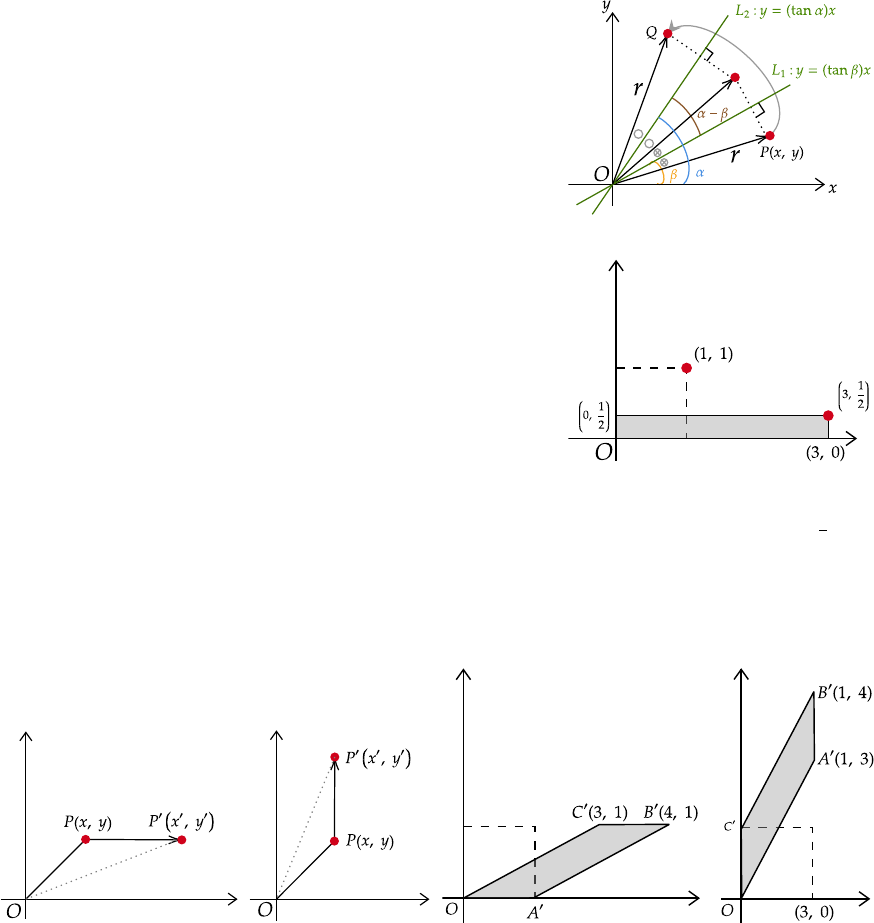
7.1 平面上基本的线性变换
x
′
= r cos(2θ − α)
y
′
= r sin(2θ − α)
⇒
x
′
= r(cos 2θ cos α + sin 2θ sin α) = x cos 2θ + y sin 2θ
y
′
= r(sin 2θ cos α − cos 2θ sin α) = x sin 2θ − y cos 2θ
可以记为矩阵形式:
x
′
y
′
=
cos 2θ sin 2θ
sin 2θ −cos 2θ
x
y
。其中,称
cos 2θ sin 2θ
sin 2θ −cos 2θ
为镜
射矩阵,表示点 P 对过原点且与 x 轴正向夹角为 θ 的直线 L 作镜射变换。
注意的是,若考虑两次的镜射变换
cos 2α sin 2α
sin 2α −cos 2α
cos 2β sin 2β
sin 2β −cos 2β
x
y
=
cos 2α cos 2β + sin 2α sin 2β cos 2α sin 2β − sin 2α cos 2β
sin 2α cos 2β − cos 2α sin 2β cos 2α cos 2β + sin 2α sin 2β
x
y
=
cos 2(α − β) −sin 2(α − β)
sin 2(α − β) cos 2(α − β)
x
y
图 7.3: Twice Reection
图 7.4: Scaling
长方形是正方形以原点 O 为中心,沿 x 轴
方向伸缩 3 倍;沿 y 轴方向伸缩
1
2
倍而得。
换言之,两次的镜射变换会合成一次的旋转变换,透过图
形的观察会更直观,请见图7.3。
7.1.3 伸缩变换
在坐标平面上,以原点 O 为中心,将点 P (x, y) 沿 x 轴方
向伸缩 h 倍 (h > 0),沿 y 轴方向伸缩 k 倍 (k > 0) 得点
P
′
(x
′
, y
′
) ,则
x
′
= hx
y
′
= ky
。若以矩阵表示
x
′
y
′
=
h 0
0 k
x
y
因此,以原点 O 为中心,将点 P (x, y) 沿 x 轴方向伸缩 h
倍 (h > 0) ,沿 y 轴方向伸缩 k 倍 (k > 0) 的伸缩变换之
表示矩阵为
h 0
0 k
, 并且
h 0
0 k
被称为伸缩矩阵。
7.1.4 推移变换
(a) (b)
图 7.5: Shear
如图7.5(a),推移变换分成沿 x 轴方向和沿 y 轴方向两种不同的情形。若点 P (x, y) 的纵坐标不
变,沿 x 轴方向推移 y 坐标的 k 倍 (k 为常数 ),得到对应点 P
′
(x
′
, y
′
), 则
x
′
= x + ky,
y
′
= y
,用
矩阵表示为
x
′
y
′
=
1 k
0 1
x
y
, 并称
1 k
0 1
为沿 x 轴方向的推移矩阵。
若是点 P (x, y) 的横坐标不变,沿 y 轴方向推移 x 坐标的 k 倍 (k 为常数 ) ,得点 P
′
(x
′
, y
′
) ,
98
7.1 平面上基本的线性变换
则
x
′
= x
y
′
= y + kx
,用矩阵表示为
x
′
y
′
=
1 0
k 1
x
y
,并称
1 0
k 1
为沿 y 轴方向的推
移矩阵。
由图如图7.5(b) 中可以看到很清楚,正方形沿 x 轴方向推移 y 坐标的 3 倍的推移变换,与沿 y
轴方向推移 x 坐标的 3 倍的推移变换,结果大不相同。不过,却也看到推移变换会改变几何图
形的形状,但不改变其面积,这由推移矩阵的行列式值为 1 也可得知。
7.1.5 线性变换的表示与矩阵乘法的诞生
容易发现,这些看似不同的运动变换,都以原点(固定点)为参考点,且变换前后坐标的表示法
中有着共同的模式:
x
′
= ax + by
y
′
= cx + dy
(1)
换而言之,新坐标可以表示为旧坐标的线性组合。这正是 Hermann Graßmann 将之命名为线性
映射的原因。事实上,如果不指出 (1) 式表示平面上的某种线性变换,我们可能会以为 (1) 式是
一个线性方程组。这并不是形式上的巧合,显然,线性方程组可以视为未知量系数的线性组合。
通过线性组合这个线索,我们就可以将线性方程和线性变换串起来,线性方程便可从线性变换的
角度来考察。
我们可以用矩阵
a c
b d
来记录类似 (1) 式这样的变换,这和使用矩阵表示一个线性方程组
是一样的,但矩阵的含义并不仅限于作为一种简记符号。即使是不了解矩阵运算规则的中学生,
在对比 (1) 式和 (2) 式之后,也会认为似乎将 (2) 式应用某种运算规则就可以得到 (1) 式。
x
′
y
′
=
a c
b d
x
y
(2)
我们现在已经知道,对 (2) 式使用矩阵乘法便可得到 (1) 式。但矩阵一开始作为一种简记符号,
是没有被定义乘法运算的,定义矩阵乘法的历史过程并不像上面描述的这么轻松。发明四元数、
也研究平面变换的 hermann graßmann 并没有定义矩阵乘法,而后来 James Joseph Sylvester 引
入 matrix 这个名词,但他也没有为矩阵定义乘法。再后来,英国数学家凯莱 (Arthur Cayley)
在研究线性变换时,为了化简线性变换的描述和书写,将形如 (1) 式的线性变换记作一个矩阵。
在 1855 年某日,凯莱考虑两个线性变换
1
与
2
1
:
x
′
= px + qy
y
′
= rx + sy
2
:
x
′
= px + qy
y
′
= rx + sy
如果将平面上的点 (x, y) 先经过 1 的变换,再经过 2 的变换后得到另一个点 (x
′′
, y
′′
) 时,整理
(x
′′
, y
′′
) 与 (x, y) 的关系,得到
x
′′
= ax
′
+ by
′
= a(px + qy) + b(rx + sy) = (ap + br)x + (aq + bs)y
y
′′
= cx
′
+ dy
′
= c(px + qy) + d(rx + sy) = (cp + dr)x + (cq + ds)y
即
x
′′
= (ap + br)x + (aq + bs)y
y
′′
= (cp + dr)x + (cq + ds)y
才气洋溢的凯莱大胆构思, 令
F =
a b
c d
, G =
p q
r s
, H =
ap + br aq + bs
cp + dr cq + ds
将上述的变换过程以矩阵 F 和 G 乘开等于 H 表示,他兴奋地写下:
99

7.2 线性映射的定义与性质
a b
c d
p q
r s
=
ap + br aq + bs
cp + dr cq + ds
于是矩阵乘法的运算规则诞生了。
7.1.6 线性变换的分解
基于矩阵乘法的定义,平面上的任意一个线性变换都可以用一个矩阵来表示。同时,5.7节(初
等矩阵)说明了任意一个矩阵都可以分解为一系列初等矩阵与一个等价标准形的乘积。
对比平面上四种基本变换的矩阵和初等矩阵,容易发现,倍乘矩阵就是伸缩矩阵,倍加矩阵就是
推移矩阵,对换矩阵是
π
4
的镜射矩阵。因此,平面上任意可逆的线性变换(二阶可逆方阵)都
可以表示成伸缩、推移和镜射变换的合成。
7.2 线性映射的定义与性质
通过前面章节的叙述,我们已经知道线性变换 A 可以用一个矩阵 A 来刻画,对某个矩阵或向
量 B 施行线性变换 A ,也就是让 A 对 B 作乘法,乘积 AB 就是线性变换的结果。因为线性
方程组也可以用矩阵乘法来表示,因此,线性方程组可以视作线性变换。
实际上,虽然不能说线性变换无处不在,但可以说线性变换几乎无处不在。可能我们没有接触太
多的实际应用,这一点没有直观的感受,但我们应该能知道线性方程组在很多领域都有应用。例
如,经济学上很多模型实际上就是在解各种各样的线性方程组。
正因为许多事物都可以抽象为线性变换,这启发我们应该将线性变换作为一个独立的数学对象
来研究。正如前面探索行列式的性质一样,我们也应该从线性变换最基本的性质入手,一步步挖
掘更多的性质。如果不知道线性变换有什么基本性质,可以回顾一下矩阵(向量)乘法的性质
(结合律、分配律)以及矩阵数乘的性质。
定义7.1 变换: 线性空间 V 到自身的映射称为 V 的一个变换。
因为,我们已经将变换定义为一个映射,而映射已经包含了结合律的性质,因此只需从分配律和
数乘的性质中抽象出线性变换的基本性质即可。
定义7.2 线性映射 (linear mapping): 设 V 和 W 是域 F 上的向量空间,A : V 7−→ W 是一
个映射。若 A 与向量空间的运算相容(或者说 A 保持向量的加法运算与数量乘法运算),即
∀α, β ∈ V, ∀k ∈ F ,
A (α + β) = A (α) + A (β)
A (kα) = kA (α)
则称 A 为线性映射,或向量空间的同态。
定义7.3 线性变换 (linear transformation): V 是域 F 上的线性空间,线性映射 A : V 7−→ V
称为线性空间 V 上的线性变换。
一般用花体拉丁字母 A , B, ··· 或小写希腊字母表示 V 的线性变换,A (α) 或 A α 代表元素 α
在线性映射 A 下的像。
这里要指出,对于映射 A : V 7−→ W ,其中 V 是域 F 上的线性空间,若 A 保持向量的加法与
数乘运算,则域 F 上的集合 W 也(可以)构成一个线性空间是自明的。这很容易证明,因此,
对于线性映射 A : V 7−→ W ,我们可以直接说中 V 和 W 都是域 F 上的线性空间。
而对于线性变换 A : V 7−→ V ,A 将 V 映射到自身是需要定义的。因为我们无法根据线性映射
保持向量的加法与数量乘法这两个条件,推导出 A 的定义域和陪域是相等的。因此,严格来说,
线性映射和线性变换是有区别的。但也很多人对这两个术语是不作区分的。
100
7.2 线性映射的定义与性质
定义7.4 恒等变换: E (α) = α(α ∈ V ) 称为线性空间 V 中的恒等变换或称单位变换 E ,亦记为
I 。
定义7.5 零映射、零变换 O: 域 F 上线性空间 V 到 V
′
的一个映射如果把 V 的任一向量都映
成 V
′
的零向量,那么称它是 V 到 V
′
的零映射,记作 O。若 V = V
′
,即 O(α) = 0(α ∈ V ),
则称之为零变换。
定义7.6 数乘变换: 设 V 是数域 P 上的线性空间,k 是 P 中的某个数,定义 V 的变换如下:
α → kα, α ∈ V
这是一个线性变换,称为由数 k 决定的数乘变换,可用 K 表示。显然当 k = 1 时,是恒等变
换,当 k = 0 时,便得到零变换。
域 F 上的线性映射 A : V 7−→ V
′
具有以下性质。
性质 1
设 A : V 7−→ V
′
是线性映射,且 0 是 V 的加法单位元,0
′
是 V
′
的加法单位元,则
(i) A (0) = 0
′
,特别地,若 V = V
′
,则 A (0) = 0
(ii) A (−α ) = −A (α)
证明.
∵ 0 = 0 ·α 线性空间的性质
∴ A (0) = A (0 · α) = 0A (α) = 0
′
A (−α ) = A ((−1)α) = (−1)A (α) = −A (α)
性质 2
线性映射保持线性组合与线性关系式不变,即 β 是 α
1
, α
2
, ··· , α
r
的线性组合:
β = k
1
α
1
+ k
2
α
2
+ ··· + k
r
α
r
那么经过线性映射 A 之后,A (β) 是 A (α
1
), A (α
2
), ··· , A (α
r
) 同样的线性组合:
A (β) = k
1
A (α
1
) + k
2
A (α
2
) + ··· + k
r
A (α
r
)
证明.
A (β) = A (k
1
α
1
+ k
2
α
2
+ ··· + k
r
α
r
)
= A (k
1
α
1
) + A (k
2
α
2
) + ··· + A (k
r
α
r
)
= k
1
A (α
1
) + k
2
A (α
2
) + ··· + k
r
A (α
r
)
由此,马上可推得以下性质。
性质 3
线性映射把线性相关的向量组变成线性相关的向量组。
证明. 由性质 2 可知,如果 α
1
, α
2
, ··· , α
r
之间有一线性关系式 k
1
α
1
+ k
2
α
2
+ ··· + k
r
α
r
= 0,
那么它们的像之间也有同样的关系
k
1
A (α
1
) + k
2
A (α
2
) + ··· + k
r
A (α
r
) = A (0)
注意,性质 3 的否命题是不对的,例如零映射可以把线性无关的向量组变为线性相关的向量组。
101

7.3 线性映射的运算
7.3 线性映射的运算
设 V 和 V
′
都是域 F 上的线性空间,我们把 V 到 V
′
的所有线性映射组成的集合记作 Hom (V, V
′
);
把 V 上的所有线性变换组成的集合记作 Hom(V, V )。Hom 是 homomorphism 的缩写。下面来
讨论线性映射可以做哪些运算,进而讨论 Hom (V, V
′
) 以及 Hom(V, V ) 的结构。
设 V, U, W 都是域 F 上的线性空间,A ∈ Hom( V, U ), B ∈ Hom(U, W ) 。线性映射作为映射,有
映射的乘法,因此有乘积映射 BA,由于 A, B 都保持加法和纯量乘法运算,因此直接计算可知,
BA 也保持加法和纯量乘法运算,从而 BA 是 V 到 W 的一个线性映射。
由于映射的乘法适合结合律,不适合交换律,因此线性映射的乘法适合结合律,不适合交换律。
设 A ∈ Hom (V, V
′
),若 A 可逆,则 A 是 V 到 V
′
的一同构映射,从而 A
−1
是 V
′
到 V 的 同
构映射,于是 A
−1
∈ Hom (V
′
, V )。
设 A, B ∈ Hom (V, V
′
)。由于陪域 V
′
是线性空间,因此可以定义加法和纯量乘法如下:
(A + B)α := Aα + Bα ∀α ∈ V ;
(kA)α := k(Aα) ∀α ∈ V �
直接计算可知,A+ B, kA 都是 V 到 V
′
的线性映射。称 A+ B 是 A 与 B 的和,kA 是 k 与 A
的纯量乘积。容易验证,Hom (V, V
′
) 中,由 (11)、(12) 式定义的加法与纯量乘法满足线性空间
定义中的 8 条运算法则,从而 Hom (V, V
′
) 成为域 F 上的一个线性空间。不难验证,线性映射
的乘法对于加法有左、右分配律,即设 A, B ∈ Hom(V, U),C ∈ Hom(U, W ), D ∈ Hom(M, V ),
则
C( A + B) = CA + CB, (A + B)D = AD + BD.
特别地, Hom(V, V ) 成为域 F 上的线性空间, 而且 Hom(V, V ) 还有乘法运算, 容易 验证, Hom(V, V )
对于加法和乘法运算成为一个有单位元的环, 还可证明线性变换的乘 法与纯量乘法满足:
定义7.7 线性变换的乘积: 设 A , B 是线性空间 V 的两个线性变换,定义它们的乘积为
(A B)(α) = A (B(α))(α ∈ V)
命题 7.1 线性变换的乘积也是线性变换。
证明.
(A B)(α + β) = A (B(α + β)) 线性变换乘积的定义
= A (B(α) + B(β)) ∵ (B(α) + B(β)) ∈ V
= A (B(α)) + A (B(β)) 线性变换乘积的定义
= (A B)(α) + (A B)(β)
(A B)(kα) = A (B(kα)) 线性变换乘积的定义
= A (kB(α)) 线性变换的定义
= kA (B(α)) ∵ B(α) ∈ V
= k(A B)(α)
命题 7.2 线性变换的乘积满足结合律:(A B)C = A (BC )
这是显然的,因为映射的乘法满足结合律,而线性变换属于映射。但线性变换的乘法不适合交换
律。例如,在实数域上的线性空间中,求导与积分一般不可以交换次序。
定义7.8 线性变换的和: 设 A , B 是线性空间 V 的两个线性变换,定义它们的和为
(A + B)(α) = A (α) + B(α)
102

7.3 线性映射的运算
命题 7.3 线性变换的和也是线性变换。
证明.
(A + B)(α + β) = A (α + β) + B(α + β)
= A (α) + A (β) + B(α) + B(β)
(
A
+
B
)(
α
) + (
A
+
B
)(
β
)
(A + B)(kα) = A (kα) + B(kα)
= kA (α) + kB(α)
∵ A (α), B(α) ∈ V
根据线性空间的左分配律,有
= k(A (α) + B(α))
= k(A + B)(α)
命题 7.4 线性变换的加法适合结合律与交换律。
A + (B + C ) = (A + B) + C
A + B = B + A
对于加法,零变换 O 与所有线性变换 A 的和仍等于 A :
A + O = A
于是,对于每个线性变换 A ,可以定义它的负变换 −A 。
定义7.9 负变换 −A :
(−A )(α) = −A (α)
A + (−A ) = O
命题 7.5 复变换也是线性的。
命题 7.6 线性变换的乘法对加法有左右分配律,即
A (B + C ) = A B + A C
(B + C )A = BA + C A
证明.
A (B + C )(α) = A (B(α) + C (α))
= A (B(α)) + A (C (α))
= (A B)(α) + (A C )(α)
(B + C )A (α) = (B(A α) + C (A α))
= (BA )(α) + (C A )(α)
定义7.10 数量乘法: 数域 P 中每个数 k 都决定一个数乘变换 K ,于是利用数乘变换和已定义
的线性变换乘法,可定义数域 P 中的数与线性变换的数量乘法为
kA = K A
即
103

7.3 线性映射的运算
kA (α) = K (A (α)) = K A (α)
根据上面的定义,数量乘法本质上就是线性变换的乘积,因此数量乘法也是线性变换。
线性变换的数量乘法适合以下的规律:
◦ (kl)A = k(lA )
◦ (k + l)A = kA + lA
◦ k(A + B) = kA + kB
◦ 1A = A
到此,我们已经定义了线性变换的加法、乘法、数乘三种运算,由加法与数乘的性质可知,线性
空间 V 上的全体线性变换,对于如上定义的加法与数量乘法,也构成数域 P 上一个线性空间。
定义7.11 逆变换: V 的变换 A 称为可逆的,如果有 V 的变换 B 存在,使得
A B = BA = E
变换 B 则称为 A 的逆变换,记为 A
−1
。
命题 7.7 如果线性变换 A 是可逆的,那么它的逆变换 A
−1
也是线性变换。
证明.
A
−
1
(α + β) = A
−
1
((A A
−
1
)(α) + (A A
−
1
)(β))
= A
−1
(A (A
−1
(α)) + A (A
−1
(β))
= A
−1
(A (( A
−1
(α)) + (A
−1
(β)))
= A
−1
A (A
−1
(α) + A
−1
(β))
= A
−1
(α) + A
−1
(β)
A
−1
(kα) = A
−1
(k(A A
−1
)(α))
= A
−1
(k(A (A
−1
)(α)))
= A
−1
(A (k(A
−1
)(α)))
= A
−1
A (k(A
−1
)(α))
= k(A
−1
)(α)
因为线性变换的乘法满足结合律,当若干个线性变换 A 重复相乘时,其最终结果是完全确定的,
与乘法的结合方法无关。则线性变换的幂可以定义如下:
定义7.12 线性变换的幂: 当 n 个(n 是正整数)线性变换 A 相乘时,用
n
z }| {
A A ···A
来表示,这称为 A 的 n 次幂,简记为 A
n
。
◦ 定义为 A 的 0 次幂为 E ,即 A
0
= E
◦ 根据线性变换幂的定义,可以推出指数法则:
A
m+n
= A
m
A
n
, (A
m
)
n
= A
mn
(m, n ≥ 0)
◦ 当线性变换 A 可逆时,定义 A 的负整数幂为 A
−n
= (A
−1
)
n
(n是正整数)
◦ 线性变换乘积的指数法则不成立,即一般说来 (A B)
n
6= A
n
B
n
定义7.13 线性变换多项式: 设 f(x) = a
m
x
m
+ a
m−1
x
m−1
+ ···+ a
0
是 P [x] 中一多项式,A 是
104

7.4 线性映射和线性变换的矩阵表示
V 的一个线性变换,定义
f(A) = a
m
A
m
+ a
m−1
A
m−1
+ … + a
0
E
显然 f(A) 是一线性变换,它称为线性变换 A 的多项式
命题 7.8 线性变换的多项式的乘法是可交换的,即在 P [x] 中 h(x) = f(x)+g(x), p(x) = f(x)g(x) ,
那么 h(A ) = f (A ) + g(A ), p(A ) = f (A )g(A )
f(A )g(A ) = g(A )f(A )
7.4 线性映射和线性变换的矩阵表示
设 V 是数域 P 上 n 维线性空间,ε
1
, ε
2
, ··· , ε
n
是 V 的一组基,A 是线性空间 V 到 V
′
的线
性映射。空间 V 中任意一个向量 α 都可以被基 ε
1
, ε
2
, ··· , ε
n
线性表出,即有关系式:
α = x
1
ε
1
+ x
2
ε
2
+ ··· + x
n
ε
n
其中系数是唯一确定的,它们就是 α 在这组基下的坐标。因为线性映射保持线性关系不变,所
以 α 的像 A α 与基的像 A ε
1
, A ε
2
, ··· , A ε
n
之间有相同的线性关系:
A α = A (x
1
ε
1
+ x
2
ε
2
+ ··· + x
n
ε
n
) = x
1
A ε
1
+ x
2
A ε
2
+ ··· + x
n
A ε
n
(7.1)
上式说明,如果知道了基 ε
1
, ε
2
, ··· , ε
n
的像,那么线性空间 V 中任意一个向量 α 在 A 下的
像 A α 也就知道了,即 n 维线性空间 V 到 V
′
的线性映射完全被它在 V 的一组基上的作用所
决定。换而言之,有如下命题:
命题 7.9 设 ε
1
, ε
2
, ··· , ε
n
是线性空间 V 的一组基,如果从 V 到 V
′
的两个线性映射 A 与 B
在这组基上的作用相同,即
A ε
i
= Bε
i
, i = 1, 2, ··· , n
那么 A = B。
证明. 要证明 A = B,即是证明 ∀α ∈ V ,A α = Bα。α 可由 V 的一组基线性表出:
α = x
1
ε
1
+ x
2
ε
2
+ ··· + x
n
ε
n
因为线性映射 A 与 B 在基 ε
1
, ε
2
, ··· , ε
n
上的作用相同,立马得出:
A α = x
1
A ε
1
+ x
2
A ε
2
+ ··· + x
n
A ε
n
= x
1
Bε
1
+ x
2
Bε
2
+ ··· + x
n
Bε
n
= Bα
命题 7.10 设 V 和 W 都是域 F 上线性空间,且 V 是 n 维的(即有限维)。ε
1
, ε
2
, ··· , ε
n
是 V
的一组基,对于 W 中任意 n 个向量 w
1
, w
2
, ··· , w
n
(它们中可以有相同的),一定存在一个线
性映射 A
A : V 7−→ W
α =
n
X
i=1
x
i
ε
i
7−→
n
X
i=1
x
i
w
i
, ∀x
i
∈ F (1)
且 A 满足 A ε
i
= w
i
, i = 1, 2, ··· , n。
证明. (1) 式是我们构造的一个对应法则 A 。因为 V 、W 和 F 是假设已经存在的,且根据线性
105

7.4 线性映射和线性变换的矩阵表示
空间的八个规则,向量的线性组合在线性空间中是存在的。又根据线性无关、线性相关的内容
可知,有限维线性空间中任意一个向量可通过基向量组的线性组合表示。因此,(1) 式是存在的。
我们要证明 A 是一个映射,且具有线性性质。
先来证明 A 是一个映射。因为 x
1
�x
2
, ··· , x
n
是 F 中的任意元素,且 ε
1
, ε
2
, ··· , ε
n
是 V 的一
组基,所以 α 是 V 任意一个向量。又因为基向量组是线性无关的,所以 α 表示成 ε
1
, ε
2
, ··· , ε
n
的线性组合的方式是唯一的,即表明 V 中任意一个向量在法则 A 下都有像,且像是唯一的。因
此,A 的确是 V 到 W 的一个映射。
再来证明 A 是线性的。在 V 中任取两个向量,
β =
n
X
i=1
b
i
ε
i
, γ =
n
X
i=1
r
i
ε
i
于是
β
+
γ
=
n
X
i=1
(
b
i
+
r
i
)
ε
i
kβ =
n
X
i=1
kb
i
ε
i
按照 (1) 式所定义的映射 A ,有
A (β + γ) = A (
n
X
i=1
(b
i
+ r
i
)ε
i
)
=
n
X
i=1
(b
i
+ r
i
)w
i
=
n
X
i=1
b
i
w
i
+
n
X
i=1
r
i
w
i
= A (β) + A (γ)
A (kβ) =
n
X
i=1
kb
i
w
i
= k
n
X
i=1
b
i
w
i
= kA (β)
因此,A 是线性映射。再来证明 A ε
i
= w
i
, i = 1, 2, ··· , n。因为
ε
i
= 0ε
1
+ ··· + 0ε
i−1
+ 1ε
i
+ 0ε
i+1
+ ··· + 0ε
n
所以
A ε
i
= 0w
1
+ ··· + 0w
i−1
+ 1w
i
+ 0w
i+1
+ ··· + 0w
n
= w
i
上述命题告诉我们,n 维线性空间 V 到 W 的线性映射 A 可以将 V 中任意 n 个线性无关的向
量分别映射为 W 中任意的向量,而 V 中这 n 个线性无关的向量的像就决定了线性映射 A ,因
此,V 中其余向量的像受到了法则 A 的约束,不能再是 W 中任意的向量。
基于以上两个命题的讨论,我们马上可以得出如下定理:
定理 7.1
设 V 和 W 都是域 F 上线性空间,且 V 是 n 维的(即有限维)。ε
1
, ε
2
, ··· , ε
n
是 V 的
一组基,对于 W 中任意 n 个向量 w
1
, w
2
, ··· , w
n
(它们中可以有相同的),存在唯一的
线性映射 A 使得
A ε
i
= w
i
, i = 1, 2, ··· , n
证明. 定理的存在性部分可以由命题7.10得到。定理的唯一性部分可以由命题7.9得到,即假设 V
106
7.4 线性映射和线性变换的矩阵表示
到 W 上的两个线性变换 A 和 B 满足
A ε
i
= w
i
, i = 1, 2, ··· , n
Bε
i
= w
i
, i = 1, 2, ··· , n
则
A ε
i
= w
i
= Bε
i
i = 1, 2, ··· , n
因此,A = B。
定义7.14 线性映射的矩阵表示: 设 V 和 V
′
都是域 F 上有限维线性空间,dim V = n, dim V
′
=
s。设 A 是 V 到 V
′
的一个线性映射。我们知道,A 被它在 V 的一个基上的作用所决定,于是
取 V 的一个基 α
1
, α
2
, ··· , α
n
,A 完全被 Aα
1
, Aα
2
, ··· , Aα
n
决定。由于 Aα
i
∈ V
′
,因此在
V
′
中取一个基 η
1
, η
2
, ··· , η
s
,Aα
i
被它在基 η
1
, η
2
, ··· , η
s
下的坐标所决定,于是有
A α
1
= a
11
η
1
+ a
21
η
2
+ ··· + a
s1
η
s
A α
2
= a
12
η
1
+ a
22
η
2
+ ··· + a
s2
η
s
.
.
.
A α
n
= a
1n
η
1
+ a
2n
η
2
+ ··· + a
sn
η
s
用矩阵来表示就是
(Aα
1
, Aα
2
, ··· , Aα
n
) = (η
1
, η
2
, ··· , η
s
)
a
11
a
12
··· a
1n
a
21
a
22
··· a
2n
.
.
.
.
.
.
.
.
.
a
s1
a
s2
··· a
sn
(1)
把 (1) 式右端的 s × n 矩阵记作 A,它的第 j 列就是 Aα
j
在 V
′
的基 η
1
, η
2
, ··· , η
s
下的坐标。
因此矩阵 A 完全被线性映射 A 和 V 的基 α
1
, α
2
, ··· , α
n
和 V
′
的基 η
1
, η
2
, ··· , η
s
所决定,称
A 是线性映射 A 在 V 的基 α
1
, α
2
, ··· , α
n
和 V
′
的基 η
1
, η
2
, ··· , η
s
下的矩阵。于是线性映射
A 有了矩阵表示。
换而言之,若 A 是 V 到 V
′
的任意一个线性映射,α
1
, α
2
, ··· , α
n
和 η
1
, η
2
, ··· , η
s
分别是 V
和 V
′
的任意一组基,由 (1) 式确立的对应关系实际上是一个映射 φ。
A : V 7−→ V
′
, dim V = n, dim V
′
= s
φ : Hom(V, V
′
)
×
Basis(V )
×
Basis(V
′
) 7−→ F
s×n
其中,Basis(V ) 和 Basis(V
′
) 分别代表 V 和 V
′
中所有基的集合。φ 是一个满射,但考虑零映射
的情况可知,φ 不是单射。在确定 V 和 V
′
的基之后,则 (1) 式建立了一个双射 σ:
A : V 7−→ V
′
, dim V = n, dim V
′
= s
σ : Hom(V, V
′
) 7−→ F
s×n
由命题7.9可知,σ 是一个单射,由命题7.10可知,σ 是一个满射,因此 σ 是一个双射。
定义7.15 线性变换的矩阵表示: 设 V 是数域数域 P 上 n 维线性空间,A 是 V 上的一个线性
变换,ε
1
, ε
2
, ··· , ε
n
是 V 的一组基。该组基向量的像可以被自身线性表出,用矩阵来表示就是
(A ε
1
, A ε
2
, ··· , A ε
n
) = (ε
1
, ε
2
, ··· , ε
n
)
a
11
a
12
··· a
1n
a
21
a
22
··· a
2n
.
.
.
.
.
.
.
.
.
a
n1
a
n2
··· a
nn
(2)
其中 (2) 式右端的 n 级矩阵记作 A。矩阵 A 完全被线性变换 A 和 V 的基 ε
1
, ε
2
, ··· , ε
n
所决
107

7.4 线性映射和线性变换的矩阵表示
定,矩阵 A 称为 A 在基 ε
1
, ε
2
, ··· , ε
n
下的矩阵。
同样地,在取定一组基之后,我们就建立了由数域 P 上的 n 维线性空间 V 的线性变换到数域
P 上的 n × n 矩阵的一个双射 σ。
A : V 7−→ V, dim V = n
σ : Hom(V, V ) 7−→ F
n×n
这个双射 σ 的重要性表现在它是 Hom(V, V ) 到 F
n×n
的同构映射,即它保持 Hom(V, V ) 中的
运算。即有以下两个定理。
定理 7.2
设 V 和 V
′
分别是域 F 上 n 维、s 维线性空间,则 V 到 V
′
的线性映射 A 与它在 V 的
一个基和 V
′
的一个基下的矩阵 A 的对应是线性空间 Hom (V, V
′
) 到 M
s×n
(F ) 的一个同
构映射,从而
Hom (V, V
′
)
∼
=
M
s×n
(F )
dim (V, V
′
)) = sn = (dim V ) (dim V
′
) �
特别地,有
Hom(V, V )
∼
=
M
n
(F )
dim(Hom(V, V )) = (dim V )
2
�
证明. 由上面的讨论,我们已经知道,当选定 V 中的一组基 α
1
, α
2
, ··· , α
s
和 V
′
中的一组基
η
1
, η
2
, ··· , η
s
后,σ 是一个双射。
A : V 7−→ V
′
, dim V = n, dim V
′
= s
σ : Hom(V, V
′
) 7−→ M
s×n
(F )
要证明 σ 是一个同构映射,只需要再证明 σ 保持向量加法和数量乘法运算。
(A + B) ( α
1
, α
2
, ··· , α
n
) = ((A + B)α
1
, (A + B) α
2
, ··· , (A + B)α
n
)
= (Aα
1
+ Bα
1
, Aα
2
+ Bα
2
, ··· , Aα
n
+ Bα
n
)
= (Aα
1
, Aα
2
, ··· , Aα
n
) + (Bα
1
, Bα
2
, ··· , Bα
n
)
= (η
1
, η
2
, ··· , η
s
) A + (η
1
, η
2
, ··· , η
s
) B
= (η
1
, η
2
, ··· , η
s
) (A + B)
因此 A + B 在 V 的基 α
1
, α
2
, ··· , α
n
和 V
′
的基 η
1
, η
2
, ··· , η
s
下的矩阵是 A + B,从而
σ(A + B) = A + B = σ(A) + σ(B)�
对于 k ∈ F ,有
(kA) (α
1
, α
2
, ··· , α
n
) = (kAα
1
, kAα
2
, ··· , kAα
n
)
= k (Aα
1
, Aα
2
, ··· , Aα
n
)
= k [(η
1
, η
2
, ··· , η
s
) A]
= (η
1
, η
2
, ··· , η
s
) (kA)
因此 kA 在 V 的基 α
1
, α
2
, ··· , α
n
和 V
′
的基 η
1
, η
2
, ··· , η
s
下的矩阵是 kA,从而
σ(kA) = kA = kσ(A)。
综上所述,σ 是域 F 上线性空间 Hom (V, V
′
) 到 M
s×n
(F ) 的一个同构映射。
Hom(V, V ) 与 M
n
(F ) 都是域 F 上的代数,即它们都有加法、纯量乘法、乘法运算。我们自然要
问: V 上的线性变换 A 对应于它在 V 的一个基 α
1
, α
2
, ··· , α
n
下的矩阵 A,是否保持乘法运
算?
108
7.4 线性映射和线性变换的矩阵表示
定理 7.3
设
V
是域
F
上
n
维线性空间,
V
上线性变换
A
与它在
V
的一个基下的矩阵
A
的对应
是代数 Hom(V, V ) 到 M
n
(F ) 的一个同构映射,从而代数 Hom(V, V ) 与 M
n
(F ) 是同构
的。
证明. 设 B = (b
ij
),由于
(AB) (α
1
, α
2
, ··· , α
n
)
=
A
(
B
α
1
,
B
α
2
,
···
,
B
α
n
)
= A
[(
α
1
, α
2
, ··· , α
n
) B
]
= A(b
11
α
1
+ b
21
α
2
+ ··· + b
n1
α
n
, ··· , b
1n
α
1
+ b
2n
α
2
+ ··· + b
nn
α
n
)
= (b
11
Aα
1
+ b
21
Aα
2
+ ··· + b
n1
Aα
n
, ··· , b
1n
Aα
1
+ b
2n
Aα
2
+ ··· + b
nn
Aα
n
)
= (Aα
1
, Aα
2
, ··· , Aα
n
) B
= [(α
1
, α
2
, ··· , α
n
) A] B
= (α
1
, α
2
, ··· , α
n
) (AB)
因此 AB 在基 α
1
, α
2
, ··· , α
n
下的矩阵是 AB,从而
σ(AB) = AB = σ(A)σ(B)。
因此 σ 是环 Hom(V, V ) 到 M
n
(F ) 的一个同构映射。
由于线性变换 A 与它在 V 的一个基下的矩阵 A 的对应是代数同构映射,因此 Hom(V, V ) 与
M
n
(F ) 的对应元素之间有关加法、纯量乘法、乘法运算的性质是一样的。例如,我们可以轻松
证明以下命题。
命题 7.11 恒等变换 I 对应于单位矩阵 I。
命题
7.12
线性变换
A
可逆当且仅当它在
V
的一个基下的矩阵
A
可逆,且
A
−1
在
V
的这个
基下的矩阵是 A
−1
。
证明. V 上的线性变换 A 可逆
⇐⇒ 存在 V 上的线性变换 B,使得 AB = BA = I
⇐⇒ 存在域 F 上的 n 级矩阵 B,使得 AB = BA = I
⇐⇒ 矩阵 A 可逆。
从这个推导过程还可看出,A
−1
= B 当且仅当 A
−1
= B。于是 A
−1
在 V 的这个基下的矩阵是
A
−1
。
命题 7.13 A 是幂等变换当且仅当它在 V 的一个基下的矩阵 A 是幂等矩阵。
证明
.
V
上的线性变换
A
是幂等变换
⇐⇒ A
2
= A
⇐⇒
A
2
=
A
⇐⇒ A 是幂等矩阵。
综上所述,我们有以下结论:V 是数域 P 上的 n 维线性空间,选定 V 的一组基,在这组基下,
每个线性变换按公式 (2) 对应一个 n × n 矩阵。这个对应具有以下的性质:
1. 线性变换的和对应于矩阵的和;
2. 线性变换的数量乘积对应于矩阵的数量乘积;
3. 线性变换的乘积对应于矩阵的乘积;
4. 可逆的线性变换与可逆矩阵对应,且逆变换对应于逆矩阵。
109
7.4 线性映射和线性变换的矩阵表示
三、向量在线性映射 (或线性变换) 下的象的坐标
线性空间 V 中取一个基 α
1
, α
2
, ··· , α
n
,V 上的线性变换 A 在此基下的矩阵为 A,V 中向
量 α 在此基下的坐标记作 x。我们自然要问:向量 Aα 在此基下的坐标是什么?由于 α =
(
α
1
, α
2
, ··· , α
n
) x,因此
Aα = A[(α
1
, α
2
, ··· , α
n
) x] = [A(α
1
, α
2
, ··· , α
n
)] x
= [(α
1
, α
2
, ··· , α
n
) A] x = (α
1
, α
2
, ··· , α
n
) Ax
从而 Aα 在基 α
1
, α
2
, ··· , α
n
下的坐标为 Ax。由于 V 中两个向量相等当且仅当它们在 V 的
一个基下的坐标相等,因此如果向量 γ 在基 α
1
, α
2
, ··· , α
n
下的坐标为 y,则
Aα = γ ⇐⇒ Ax = y
◦
对于向量在线性映射下的象的坐标也有类似的结论:
定理 3 表明: 同一个线性变换 A 在 V 的不同基下的矩阵是相似的,这就是我们在本套教材上册
第 5 章相当多的篇幅讨论 n 级矩阵的相似关系的主要原因。反之,设域 F 上的 n 级矩阵 A 与
B 相似,则存在域 F 上的 n 级可逆矩阵 P ,使得 B = P
−1
AP 。设 V 是域 F 上的 n 维线性
空间,V 中取一个基 α
1
, ··· , α
n
。根据本节定理 1,存在 V 上唯一的线性变换 A 使得 A 在基
α
1
, ··· , α
n
下的矩阵为 A。令
(
η
1
, ··· , η
n
) = (α
1
, ··· , α
n
) P ,由于 P 可逆,因此 η
1
, ··· , η
n
是
V 的一个基。根据定理 3, A 在基 η
1
, ··· , η
n
下的矩阵为 P
−1
AP ,它等于 B。因此相似的矩阵
可以看成是线性空间 V 上同一个线性变换 A 在 V 的不同基下的矩阵。由于 n 维线性空间 V
上的线性变换 A 在 V 的不同基下的矩阵是相似的,而 n 级矩阵的行列式、秩、迹都是相似关
系下的不变量,因此我们把 A 在 V 的一个基下的矩阵 A 的行
110
第八章 附录
8.1 附录 I 线性代数的含义
既然要学习线性代数,当然要知道线性代数是什么。然而大部分教材可能只有书的封面会出现线
性代数这四个字,一遍读下来,还是不知道线性代数是什么。不难理解,线性代数包含了两个词:
线性和代数。线性在这里是一个形容词,完整来说,应该是线性的代数(有线性性质的代数)。
线性一词可能是由英文文献中的 linear 引入。linear 在英文中用于描述直线形象,以下是韦伯斯
特词典的第一条解释:
of, relating to, resembling, or having a graph that is a line and especially a straight
line : STRAIGHT
根据 Google 提供的网页词典,linear 的词源:
mid 17th century: from Latin linearis, from linea ’a line’
可以猜测,数学中的 linear 实际上也是直线性质的抽象,例如线性函数的线性定义如下。
定义8.1 线性函数: 线性函数是一种线性映射,是在两个向量空间之间,维持向量加法与纯量乘
法的映射。
f(x + y) = f(x) + f(y) (可加性)
f(ax) = af(x) (齐次性)
可加性和齐次性统称为叠加原理 (Superposition principle)。可加性的物理意义是变量叠加后的
作用结果等于各个变量单独作用结果的叠加,而齐次性的物理意义是缩放变量,其作用结果也同
等比例地缩放。
定义8.2 多线性函数: 设 f(X
1
, X
2
, ··· , X
n
) 为一个以向量为变元的多元函数。若对于每一个
j(1 ≤ j ≤ n),当 X
1
, ··· , X
j−1
, X
j+1
, ··· , X
n
全部固定不动时,f 恒为 X
j
的线性函数,则称
f 为多线性函数。
linear 还有另一种常见的解释:
involving a single dimension
此时,线性是指因变量为一阶的多项式函数,即可以表示为 y = kx + b 的形式。初等数学和许
多非数学学科的书籍会习惯把这个定义当作线性关系的概念。这种术语间的细微差异如果不注
意的话,就容易引起混淆。
代数实际上是一个多义词。通常情况下,代数 (algebra) 是指「代数学」这门数学分支。而字面
上,代数又表示用符号来代替具体的数值,从而数值的运算变成符号的运算。由此,我们不再关
心具体的运算结果,只关心其中的运算规律和性质。进入抽象代数,代数可能泛指各种「代数
结构」。一个代数结构是指一个带有一种或多种运算的集合。集合上附带的运算称为这个集合的
「代数运算」。此外,代数也可能特指一个名为「代数」的代数结构。
algebra 原来并没有数学上的含义,数学含义来源于数学家 al-Ḵwārizmī 著作的名字 ilm al-jabr
111

8.2 附录 II 名词解释
wa’l-muqābala(the science of restoring what is missing and equating like with like)。如今,代
数词义的混乱可能已无法溯源。对于线性代数的初学者来说,下面这句话基本无人能懂。
「我现在学习抽象代数的代数的代数结构」
8.2 附录 II 名词解释
分离系数法 多项式除以多项式,当除式、被除式都按降幂排列时,各项的位置就可以表示所含
字母的次数。因此,计算时,只须写出系数,算出结果后,再把字母和相应的指数补上。这种方
法叫做分离系数法。参见
例:计算 (25x
4
− 41x
2
+ 7x + 16) ÷ (5x
2
+ x − 4)
5x
2
− x − 4
5x
2
+ x − 4
25x
4
− 41x
2
+ 7x + 16
− 25x
4
− 5x
3
+ 20x
2
− 5x
3
− 21x
2
+ 7x
5x
3
+ x
2
− 4x
− 20x
2
+ 3x + 16
20x
2
+ 4x − 16
7x
图 8.1: 多项式除法
论数学教育 On teaching mathematics,英译文:“The determinant of a matrix is an (oriented)
volume of the parallelepiped whose edges are its columns. If the students are told this secret
(which is carefully hidden in the puried algebraic education) , then the whole theory of deter-
minants becomes a clear chapter of the theory of poly-linear forms. If determinants are dened
otherwise, then any sensible person will forever hate all the determinants, Jacobians and the
implicit function theorem.”
求平行四边形面积 设向量 x = (a, b) 且 y = (c, d),则 x 与 y 所张的平行四边形的有号面积等
于 kxkkyk sin θ(即底乘高),其中 θ 是 x 与 y 的夹角,0 ≤ |θ| < π。这里要特别说明夹角 θ 的
正负号由 x 与 y 的相对位置决定。通用惯例采用右手座标系,也就是说,如果夹角 θ 为 x 至 y
的逆时针旋转,则 θ > 0,否则 θ < 0。考虑 x 逆时针旋转 90
◦
,设为 x
⊥
= (−b, a),则 x
⊥
与 y
的之间夹角等于
π
2
− θ。平行四边形的有号面积可用内积计算,如下:
kxkkyk sin θ = kx
⊥
kkyk cos
π
2
− θ
= x
⊥
· y = ad − bc
行列式的名字由来 行列式的英文是 determinant,意为判定,它的主要的功用之一在于判定矩
阵是否可逆。矩阵的日文是行列,行列式可能源自日文,意为矩阵式。为什么要将其译为行列式
呢?一方面,行列式的本身按行、列进行编排;另一方面,行列式这个名词提示了它所具备的三
个基本性质全都建立于行或列之上,即以行、列为基本单位,而且行与列的地位是对称的。
行列式的基础属性 行列式有 4 个基础属性:
1. 初等行变换不会改变行列式的值
2. 两行(列)交换位置,行列式变号
3. 用一个数乘以某行(列),等价于该数乘以行列式
112

8.2 附录 II 名词解释
4. 单位矩阵的行列式 I
n
等于 1
但一般定义行列式使用以下 3 个属性:
1. 行列式是多线性的
2. 若两行(列)相同,则行列式为 0
3. 单位矩阵的行列式 I
n
等于 1
可以证明上面的 4 个属性等价于下面的 3 个属性,它们可以互推。
交错性和斜对称性 直接在网上搜索 alternating property 和 skew-symmetric property,几乎
找不到完全匹配的资料。即使使用中文名词,也是空白的搜索结果,似乎很少人直接使用这样
的形容词。alternating 和 skew-symmetric 在数学上更多的是指代拥有某种性质的函数。例如,
Alternating multilinear forms、Symmetric bilinear form。
We dene a form to be
• symmetric: if B(v, w) = B(w, v) for all v, w in V ;
• alternating: if B(v, v) = 0 for all v in V ;
• skew-symmetric: if B(v, w) = −B(w, v) for all v, w in V ;
V is a vector space.
参考
1. Unimodular Form - Symmetric, Skew-symmetric and Alternating Forms
2. Bilinear form
3. Skew-symmetric matrix
4. What do mathematicians mean when they say ”form”?
欧几里得距离 在欧几里得空间中,点 x = (x
1
, . . . , x
n
) 和 y = (y
1
, . . . , y
n
) 之间的欧氏距离为
d(x, y) =
q
(x
1
− y
1
)
2
+ (x
2
− y
2
)
2
+ ··· + (x
n
− y
n
)
2
虽然欧氏距离以欧几里得的名字命名,但在《几何原本》中,欧几里得并未明确提出欧氏距离的
概念。另一方面,上述欧氏距离定义式借助了笛卡尔坐标系(直角坐标系),但笛卡尔坐标系在
17 世纪才出现。显然,欧氏距离不可能是欧几里得直接提出的。既然如此,它为何冠以欧几里
得之名,又为何是符合现实世界直觉的距离定义?
实际上,笛卡尔坐标系之中的欧氏距离本质上是勾股定理的推广或应用。应用两次勾股定理就
可以推导出三维空间的欧氏距离。虽然欧几里得并未明确提出欧氏距离的概念,但是这种思想
已经蕴含在《几何原本》之中。
勾股定理描述了三角形边长之间的关系,并且可以推广到高维空间。边长和面积的定义明显是
符合直觉的,在实数轴上,边长就是两个端点之差的绝对值,而矩形面积是长乘宽。基于这些定
义得到的勾股定理和欧氏距离自然也符合我们对现实空间中距离的感知。
叙述与命题 凡是能辨别真假的语句,称为叙述。设 P 表示一叙述,其否定叙述以 ¬P 表示,并
称之为非 P 。形如“若 ···,则 ···”形式的叙述,我们将其称为命题,并将其简写为 a ⇒ b。
设 a 和 b 为两个叙述,则“若 a 则 b”就是一个命题,其中 a 称为命题的前提(或称为假设),
b 称为命题的结论。“若 a 则 b”是一个命题,而“若 b 则 a”也是一个命题,它们互称为对方
的逆命题。命题可能是对的,也可能是错的,但一个命题无论对错,其逆命题可能是对的,也可
能是错的。
113

8.2 附录 II 名词解释
充分必要条件 当命题“若 a 则 b”正确时,我们称 a 是 b 的充分条件,同时称 b 是 a 的必要
条件。
a 是 b 的充分条件,这意味着 a 能导致 b,但或许其他条件也能导致 b,即可能有多个条件能独
立导致 b,而 a 只是其中一个。
b 是 a 的必要条件,这意味着,a 的发生可能需要 b 与其他多个条件同时成立,其中 b 是一个必
要(必需)的条件,若 b 不成立,则 a 必然不成立。换而言之,b 发生,而 a 可能不发生,因为
条件可能不足,但 a 发生,则意味着 b 一定发生。
当一个命题“若 a 则 b”与它的逆命题“若 b 则 a”都正确时,我们称为 a 和 b 互为充分必要
条件,并简写为 a ⇔ b。换而言之,“a 是 b 的充要条件”表明:b 的发生需要条件,且 a 是 b
的唯一条件。若用集合论的观点来看,这表明 a 和 b 两个集合是相等的。
充分必要条件的一个等价叙述是“当且仅当”,即以下两个命题是等价的:
1. b 成立,当且仅当 a。
2. b 的充分必要条件是 a。
单位矩阵、初等矩阵、等价标准形、行阶梯形矩阵、简约行梯矩阵
n 阶单位矩阵是一个 n × n 的方形矩阵,其主对角线的元素全为 1,其余元素全为 0。记为 I
n
或 E
n
。
初等矩阵是由单位矩阵 E 经过一次初等变换得到的矩阵,因此,初等矩阵也是满秩的方阵。
等价标准形 (equivalent canonical form) 是一个 m ×n 矩阵,其主对角线左上角的元素可以为 1
或
0
,其余元素全为
0
,可以用分块矩阵
E
(r)
m×n
表示。
E
(r)
m×n
=
E
r×r
O
r×(n− r)
O
(m−r )×r
O
(m−r )×(n −r)
行阶梯形矩阵 (row echelon form) 是具有以下特征的矩阵:
1. 全零行都在矩阵的底部,即所有非零行在所有全零行的上面。
2. 非零行的主元(首非零元;leading coecient),即最左边的首个非零元素,严格地比上面
行的主元更靠右。
3. 主元下面的元素都是零(前两条的推论)。
简约行梯矩阵(亦称为简约列阶梯矩阵、行最简形矩阵、行规范形矩阵;reduced row echelon
form, row canonical form)是满足以下额外条件的行阶梯形矩阵:
1. 主元都为 1,且是其所在列的唯一非零元素。
注意,简约行梯矩阵的左部并非总是单位矩阵。例如,如下的矩阵是简化行阶梯形矩阵:
1 0 1/2 0 b
1
0 1 −1/3 0 b
2
0 0 0 1 b
3
基于以上叙述,可以得出这五种矩阵的韦恩关系图。
矩阵 A 左乘初等矩阵,表示对矩阵 A 做初等行变换;矩阵 A 右乘初等矩阵,表示对矩阵 A 做
初等列变换。所有矩阵都可以通过初等行变换转换为行阶梯形矩阵,对行阶梯形矩阵继续做初
等行变换,可以转换为简约行梯矩阵,简约行梯矩阵做初等列变换,可以转换为等价标准形。
行阶梯形矩阵是否包含零矩阵,这取决于其定义中是否规定矩阵的行至少有一个非零元素。
114

8.3 附录 III 代数结构
1/25/2022 diagram-20220125 (1).svg
file:///C:/Users/Allen/Downloads/diagram-20220125 (1).svg 1/1
单位
矩阵
等
价
标
准
形
简
约
行
梯
矩
阵
行
阶
梯
形
矩
阵
初等
矩阵
图 8.2: 五种简单矩阵的关系
结构、空间 结构是指带有一种或多种运算的一个或多个非空集合,或者说,结构是一个或多个
非空集合,以及定义在这些集合上的一种或多种运算。例如,代数结构有群、环、域、模、向量
空间、代数等等。这些装备了运算的集合称为 underlying set 或 ground set。一般地,一个结构
可以类似地记为 (X, τ ),其中 X 是一个集合,τ 是定义在 X 上的一种运算。
空间没有太正式的定义,有人会认为空间是结构的另一种说法,其他人则认为结构和空间是不一
样的。通常,空间更具几何性,而结构更具代数性。在我看来,空间属于或类似于结构,空间有
两个或以上的集合,这些集合之间定义了相关联的运算。例如,域 F 上的线性空间 V 可以定义
数乘运算,即 F × V 7−→ V 。
8.3 附录 III 代数结构
定义8.3 笛卡儿积 (Cartesian product): 两个集合 X 和 Y 的笛卡儿积是所有可能的有序对
(x, y) 组成的集合,表示为 X
×
Y ,其中 x ∈ X, y ∈ Y 。
X
×
Y = {(x, y) | x ∈ X ∧ y ∈ Y }
定义8.4 二元运算 (Binary Operation): 定义在集合 X 上的二元运算 ∗ 可视为一个函数:
X
×
X 7−→ X
定义8.5 单位元: 设 S 是一个集合,∗ 是定义在 S 上的二元运算,即是 S
×
S 到 S 的一个映射。
S 的元 e 称为左单位元(或右单位元),若对于每个 x ∈ S,有 e ∗x(或 x ∗e)。同时是左、右单
位元的元素被称为单位元,又称为幺元、恒等元或中立元。如果 S 具有单位元,则单位元必是唯
一的。当二元运算是乘法运算时,单位元常记作 1,若是加法运算,单位元常称为零元,记作 0。
定义8.6 逆元: 设 S 是一个集合,∗ 是定义在 S 上的二元运算,关于 ∗ 运算,S 存在单位元。对
于 x ∈ S,若存在 y ∈ S,且 yx = e(或 xy = e),则称 y 是 x 的左逆元(右逆元)。若 y 同时是
x 的左、右逆元,则称 y 是 x 的逆元。此时,称 x 是可逆的,x 的逆元记为 x
−1
。若存在逆元,
逆元是唯一的。
定义8.7 群: 给定一个集合 G 与二元运算 ∗,若运算 ∗ 满足下述四个性质,即封闭性、结合性,
存在一运算单位元,且每一元素皆存在对应的逆元,我们便称 (G, ∗) 为不可交换群,或简称为
群。
1. 运算 ∗ 具有封闭性,如果 x 和 y 属于 G ,那么 x ∗ y 也属于 G。
2. 运算 ∗ 具有结合性,排序固定的三个元素的运算结果和其执行顺序无关,即 (x ∗ y) ∗ z =
x ∗ (y ∗ z),其中 x, y, z ∈ G。
3. 存在一单位元 e,使得任何元素与其运算皆不改变,即 x ∗ e = e ∗ x = x,其中 x, e ∈ G。
4. 任何元素的 ∗ 运算都可逆,即对任一元素 a 皆存在逆元 b,a∗b = b∗a = e,其中 a, b, e ∈ G。
定义8.8 半群: 给定一个集合 G 与二元运算 ∗,若 (G, ∗) 满足以下条件,我们便称它为半群
(semi-roup)。
1. 运算 ∗ 具有封闭性。
115
8.3 附录 III 代数结构
2. 运算 ∗ 具有结合性,(x ∗ y) ∗ z = x ∗ (y ∗ z)。
定义8.9 幺半群: 给定一个集合 G 与二元运算 ∗,若 (G, ∗) 满足以下条件,我们便称它为幺半
群。
1. (G, ∗) 是一个半群。
2. 存在一单位元 e,使得任何元素与其运算皆不改变,即 x ∗ e = e ∗ x = x,其中 x, e ∈ G。
定义8.10 阿贝尔群/交换群: 给定一个集合 G 与二元运算 ∗,若 (G, ∗) 满足以下条件,我们便
称它为可交换群 (commutative group),又称为阿贝尔群 (Abel group)。
1. (G, ∗) 是一个群。
2. 运算 ∗ 具有交换性,x ∗ y = y ∗ x,其中 x, y ∈ G。
定义8.11 同态与同构: 同态的意义是保持结构的映射。对于带二元运算的非空集 S
1
, S
2
,同态
φ : S
1
→ S
2
所要保持的结构无非是二元运算,即:∀x, y ∈ S
1
, φ(xy) = φ(x)φ(y)。准此要领可定
义半群的同态。然而么半群的情形更常见也更为实用,此时我们要求同态必须兼保乘法和幺元。
设 M
1
, M
2
为幺半群。映射 φ : M
1
→ M
2
如满足下述性质即称为同态
1. ∀x, y ∈ M
1
, φ(xy) = φ(x)φ(y);
2. φ(1) = 1.
从幺半群 M 映至自身的同态称为自同态,如恒等映射 id
M
: M → M 。同态的合成仍为同态。
取常值 1 的同态称作平凡同态。
若存在同态 ψ : M
2
→ M
1
使得 φψ = id
M
2
, ψφ = id
M
1
,则称 φ 可逆而 ψ 是 φ 的逆;可逆同态
称作同构,写成 φ : M
1
∼
→ M
2
。此时我们也称 M
1
与 M
2
同构。从幺半群映至自身的同构称为
自同构。同构联系了本质上相同的代数结构,即同构的对象本质上具有等价关系。
定义8.12 环: 集合 G 和定义于其上的二元运算 + 和 · 构成的三元组 (G, + , ·) 构成一个环 (ring),
若它们满足:
1. (G, +) 形成一个交换群,其单位元称为零元素,记作 0。
2. (G, ·) 形成一个半群。
3. · 关于 + 满足分配律,即
(a) a · (b + c) = (a · b) + (a · c)
(b) (a + b) · c = (a · c) + (b · c)
+ 和 · 常被简称为加法和乘法,但与一般所说的加法和乘法不同,而是广义上的加法和乘法。
只要 (G, +) 是一个群,且 · 运算对 + 运算具有分配律,那么对于 ∀a ∈ G,必然有 0 · a = 0。
换而言之,+ 运算的单位元 0 元素对于 · 运算不存在逆元。因此,(G, ·) 无法构成一个群,但
({x|x 6= 0, ∀x ∈ G}, ·) 可以构成一个群。证明过程如下:
0 · a = (0 + 0) · a
= 0 · a + 0 · a
因为 G(, +) 是一个群,所以 0 · a ∈ G 且 0 · a 对 + 具有逆元,即 0 · a + 逆元 = 0。
0 · a + 逆元 = 0 · a + 0 · a + 逆元
0 = 0 · a + 0 (单位元的性质)
0 = 0 · a
如果 · 运算是可交换的,那么也证明了 a · 0 = 0,如果 · 运算是不可交换的,也可以类似地证明
a · 0 = 0。如果要定义 a · 0 6= 0,那么 · 对 + 不能满足分配律,· 和 + 只是集合 G 上两个独立
的运算,两者没有交互。
116
因为 0 是 + 运算的单位元,所以 0+0=0
根据 · 对 + 的分配律

8.3 附录 III 代数结构
定义8.13 交换环: 集合 G 和定义于其上的二元运算 + 和 · 构成的三元组 (G, +, ·) 构成一个交
换环,若它们满足:
1. (G, + , ·) 是一个环。
2. (G, ·) 具有交换性,即 a · b = b · a,其中 a, b ∈ G。
定义8.14 零因子: 一个环的一个非零元素 a 是一个左零因子,当且仅当存在一个非零元素(零
是 + 的单位元)b,使得 a ·b = 0。类似地,一个环的一个非零元素 a 是一个右零因子,当且仅
当存在一个非零元素 b,使得 b ·a = 0。左零因子和右零因子统称为零因子 (zero divisor)。在交
换环中,左零因子和右零因子是等价的。
定义8.15 整环: 一个无零因子的有单位元的交换环称为整环,也称为整域 (intergral domain)。
定义8.16 除环: 乘法存在单位元,且所有非零元素全体对乘法构成群(也就是所有非零元素对
乘法运算存在逆元)的环称为除环 (division ring),也称为拟域 (skew eld)。有的文献也会称之
为体。
定义8.17 域: 集合 G 和定义于其上的二元运算 + 和 · 构成的三元组 (G, +, ·) 构成一个域
(eld),若它们满足:
1. (G, + , ·) 是一个交换环。
2. 存在一单位元 e,使得任何元素与 e 的 · 运算皆不改变,即 x ·e = e ·x = x,其中 x, e ∈ G。
3. 任何非零元素的 · 运算都可逆,即对任一元素 a 皆存在逆元 b,a · b = b · a = e,其中
a, b, e ∈ G。
换而言之,若 (G, +) 是一个交换群,排除零元素的 (G, ·) 也是一个交换群,则 (G, +, ·) 构成一
个域。简而言之,可交换的除环称为域。
有的文献将 eld 翻译为体,即身体的体,意为 eld 有四则运算(加减乘除),就像人体有四肢。
表 8.1: 乘法运算在各种环中的区别
结合律 封闭性 单位元 逆元 交换律
环 • •|⊖
幺环 • •|⊖ •
交换环 • •|⊖ •
无零因子环 • •|⊛
整环 • •|⊛ • •
除环 • •|⊛ • •
域 • •|⊛ • • •
⊖ 表示排除 0 后,乘法运算不满足封闭性,即非零元素相乘可能等于零。
⊛ 表示排除 0 后,乘法运算满足封闭性。
定义8.18 模: 设 R 为环,且 R 包括乘法单位元 1
R
,则左 R − 模 包括以下资料:
1. 加法群 (M, +)
2. 映射 R × M 7−→ M,记为 (r, m) 7−→ r · m(左乘),满足以下性质:
r(m
1
+ m
2
) = rm
1
+ rm
2
, r ∈ R, m
1
, m
2
∈ M
(r
1
+ r
2
)m = r
1
m + r
2
m, r
1
, r
2
∈ R, m ∈ M
(r
1
r
2
)m = r
1
(r
2
)m
1
R
· m = m
若将定义中的左乘改为右乘 (r, m) 7−→ m ·r,条件改为 m(r
1
r
2
) = (mr
1
)r
2
等等,得到的概念称
117

8.4 附录 IV 空间
为右 R − 模。一般简称 M 是左或右 R −模。因为 m 的系数 r 取自环 R,因此若环 R 是可交
换的,又称一个模为环 R 上的模,或写为 R − 模(R-module)。
模是向量空间的推广,常见的线性空间就是域上的模。比照熟悉的向量空间情形,我们也称运算
R × M → M 为 R 的纯量乘法。由以上公理容易导出在左 R-模 M 中有下述性质:
0 · m = 0, m ∈ M,
(−1
R
) · m = −m,
(n · 1
R
) · m = nm =
m + ··· + m
n 项
, n ∈ Z
≥0
,
(−n · 1
R
) · m = −(nm) .
因此形如 n·m(n ∈ Z) 的表达式没有歧义:既可视之为 (M, +) 中的倍数运算,亦可视 为 n·1
R
∈ R
的乘法作用。右模的情形类似。
定义8.19 代数: 若 F 为域,F 上的一个代数 (algebra) A 为一个非空集合 A,且有两种运算:
加法(记作 +),乘法(用毗连表示)以及 F 对 A 的运算数乘 (也用毗连表示) 满足以下规律:
1. 对加法与 F 对 A 的数乘,A 是一个向量空间;
2. 对加法与乘法,A 是一个有单位元的环;
3. 若 r ∈ F 及 a, b ∈ A,有 r(ab) = (ra)b = a(rb)。
也就是说,定义在域 F 的代数 A 是有向量乘法的向量空间(A 的元素称为向量),代数 A 也是
可以对每个元素进行数乘的环。即代数既是向量空间又同时是环,是向量空间与环的结合。
表 8.2: 不同的模的区别
Over 数乘 向量加法 向量乘法
模 环 • •
线性空间 域 • •
代数 域 • • •
8.4 附录 IV 空间
在欧式空间中一个很重要的概念就是距离(度量)。在 R
n
中我们常用的一个度量是如下的度量:
对于 x = (x
1
, x
2
, ··· , x
n
) , y = (y
1
, y
2
, ··· , y
n
) ∈ R
n
,我们取
ρ =
h
(x
1
− y
1
)
2
+ ··· + (x
n
− y
n
)
2
i
1
2
.
我们希望提炼出欧式度量的核心性质,将这个概念推广到一般的空间上去,就有了下面度量空间
的概念。
定义8.20 度量空间: 设 X 是一个非空集。称 X 为度量空间(距离空间),是指在 X 上定义
了一个双变量的实值函数 d(x, y),满足下列四个公理:
1. d(x, y) 是实值、有限和非负的
2. d(x, y) = 0,当且仅当 x = y
3. d(x, y) = d(y, x) (对称性)
4. d(x, z) ≤ d(x, y) + d(y, z)(∀x, y, z ∈ X ) (三角不等式)
这里 d 叫做 X 上的一个度量,以 d 为度量的度量空间 X 记做 (X , ρ)。
118
8.4 附录 IV 空间
我们引进了一个空间 X 的代数结构——线性空间,也引进过它的拓扑结构一距离 d,现在要把
代数结构和拓扑结构结合起来,即是要求:
距离的平移不变性:
d(x + z, y + z) = d(x, y)(∀x, y, z ∈ X ).
由此推,d 对加法是连续的,即
已有
d (x
n
, x) → 0
d (y
n
, y) → 0
推导出
=⇒ d (x
n
+ y
n
, x + y) → 0.
事实上,利用平移不变性的条件,上式推导如下
d (x
n
+ y
n
, x + y) = d ( x
n
+ y
n
− x − y, θ)
= d (x
n
− x, y − y
n
)
≤ d (x
n
− x, θ) + d (y − y
n
, θ)
= d (x
n
, x) + d (y, y
n
) → 0( 当n → ∞).
反之,如果距离 d 对加法连续,则满足平移不变性。
数乘的连续性:
1. d (x
n
, x) → 0 ⇒ d (αx
n
, αx) → 0(∀α ∈ K);
2. α
n
→ α(K) ⇒ d (α
n
x, αx) → 0(∀x ∈ X ).
若令 p : X → R
1
, p(x) := d( x, θ)(∀x ∈ X ),则由平移不变性:
p(x − y) = ρ(x − y, θ) = ρ(x, y).
这时由距离公理逐条化为函数 p 的条件:
d(x, y) ≥ 0 ⇔ p(x) ≥ 0(∀x, y ∈ X );
d(x, y) = 0, 当且仅当x = y ⇔ p(x) = 0, 当且仅当x = θ;
d(x, y) ≤ ρ(x, z) + ρ(z, y) ⇔ p(x + y) ≤ p(x) + p(y);
d(x, y) = ρ(y, x) ⇔ p(−x) = p(x).
此外,
(2.1) ⇔ p (αx
n
) → 0
当p (x
n
) → 0
;
(2.2) ⇔ p (α
n
x) → 0
当α
n
→ 0
.
定义8.21 准范数: 线性空间 X 上的准范数 (准模) 定义为这空间上的一个函数 k·k : X → R
1
,
对于 ∀x, y ∈ X 和 ∀α ∈ K,满足条件:
1. kxk ≥ 0; kxk = 0 ⇔ x = θ;
2. kx + yk ≤ kxk + kyk;
3. k − xk = kxk;
4. lim
α
n
→0
kα
n
xk = 0, lim
∥x
n
∥→0
kαx
n
k = 0.
定义8.22 范数: 线性空间 X 上的范数 k · k 是一个非负值函数: X → R
1
满足:
1. kxk ≥ 0(∀x ∈ X ); kxk = 0 ⇔ x = θ (正定性);
2. kx + yk ≤ kxk + kyk(∀x, y ∈ X ) (三角不等式);
3. kαxk = |α|kxk(∀α ∈ K, ∀x ∈ X ) (齐次性). 显然范数必是准范数.
定义8.23 赋范线性空间: 赋范线性空间就是定义了范数的线性空间。
定义8.24 共轭双线性函数: 线性空间 X 上的一个二元函数 a(·, ·) : X × X → K, 称为是共轭
119

8.5 附录 V 补充证明
双线性函数, 如果
1. a (x, α
1
y
1
+ α
2
y
2
) = ¯α
1
a (x, y
1
) + ¯α
2
a (x, y
2
) ;
2. a (α
1
x
1
+ α
2
x
2
, y) = α
1
a (x
1
, y) + α
2
a (x
2
, y),
其中 ∀x, y, x
1
, x
2
, y
1
, y
2
∈ X , ∀α
1
, α
2
∈ K. 我们还称由
q(x) := a(x, x)(∀x ∈ X )
定义的函数为 X 上由 a 诱导的二次型.
定义8.25 内积: 线性空间 X 上的一个共轭双线性函数
(·, ·) : X × X → K,
称为是一个内积, 如果它满足:
1. (x, y) = (y, x)(∀x, y ∈ X ) (共轭对称性);
2. (x, x) ≥ 0(∀x ∈ X ), (x, x) = 0 ⇔ x = θ (正定性).
具有内积的线性空间称为内积空间, 记做 (X , (·, ·)). 也用 < ·, · > 作为内积符号.
8.5 附录 V 补充证明
命题 8.1 映射 φ : X 7−→ Y 是可逆的,当且仅当 φ 是双射。
证明. 假设 φ : X 7−→ Y 是可逆的,将它的逆映射记为 φ
−1
,我们需要证明 φ 是双射。先来证
明 φ 是单射。设 a, b ∈ X 且 φ(a) = φ(b)。若 a 6= b,则 φ 不是单射,若 a = b,则 φ 是单射。
a = φ
−1
φ(a) = φ
−1
φ(b) = b
因此,证得 φ 是单射。再来证 φ 是满射。要证 φ 是满射,即是证 φ 的值域 ran φ = Y 。由集合
相等的定义,我们只需要证 ran φ ⊆ Y 且 ran φ ⊇ Y 。
因为 φ 是 X 到 Y 的映射,所以显然有 ran φ ⊆ Y 。由逆映射的定义,有
φφ
−1
(y) = y, ∀y ∈ Y
所以
ran
φ
⊇
Y
。由此证得
φ
是满射。
现在假设 φ 是双射,我们需要证明 φ 是可逆的。∀y ∈ Y ,定义 x 是 X 中使得 φ(x) = y 的那
个元素。因为 φ 既是单射,又是满射,即是一一对应的,所以此元素必定存在且是唯一的。由
此,我们可定义一个映射 σ,使得 σ(y) = x。
显然,φ(x) = φ(σ(y)) = (φσ)(y) = y,因此 φσ 是恒等映射。因为映射的乘积具有结合律,所以
(
σφ
)
σ
(
y
) =
σ
(
φσ
)(
y
) =
σ
(
y
)
因此,σφ 也是恒等映射。由逆映射的定义可知,φ 和 σ 互为逆映射,即 φ 是可逆的。
命题 8.2 ε
1
, ε
2
, ··· , ε
n
是域 P 上的线性空间 V 的一组基,V 中的向量与这组基下的坐标的对
应关系是 V 到 P
n
的一个双射。
证明. 上述命题实际上包含了以下三个命题:
1. V 中的向量与 ε
1
, ε
2
, ··· , ε
n
下的坐标的对应关系构成 V 到 P
n
的一个映射:σ : V 7−→ P
n
。
2. 映射 σ 是一个单射。
3. 映射 σ 是一个满射。
120
8.5 附录 V 补充证明
第 1、2 个命题的证明可等价地转换为以下命题的证明:
I. V 中任意向量 α 都能被 ε
1
, ε
2
, ··· , ε
n
线性表出,且表示法唯一。
实际上,命题 I 就是定理4.2。但我们前面在证明定理4.2时借助了线性方程组的内容,而所有包
含 n 个方程的 n 元线性方程组本身已经是一个特殊的 n 维线性空间。在这里,V 泛指所有线性
空间,因此,现在我们只通过线性空间的八个规则,以及线性相关(线性表出)、维数、基、坐
标的定义来证明命题 I。
假设 n 维线性空间 V 中有一个向量 α 无法由 ε
1
, ε
2
, ··· , ε
n
线性表出,则向量组 ε
1
, ε
2
, ··· , ε
n
, α
线性无关。那么,V 至少是 n + 1 维的,这与假设矛盾。因此,n 维线性空间 V 的所有向量都
能由 ε
1
, ε
2
, ··· , ε
n
线性表出。
假设 V 中有一个向量 α 能以两种表示法由 ε
1
, ε
2
, ··· , ε
n
线性表出,即
α = k
1
ε
1
+ k
2
ε
2
+ ··· + k
n
ε
n
(1)
α = l
1
ε
1
+ l
2
ε
2
+ ··· + l
n
ε
n
(2)
其中 k
1
, k
2
, ··· , k
n
与 l
1
, l
2
, ··· , l
n
不全相等。那么 α 的逆元可以表示为
−α = −1 · α
= −1 · (l
1
ε
1
+ l
2
ε
2
+ ··· + l
n
ε
n
)
= −l
1
ε
1
− l
2
ε
2
− ··· − l
n
ε
n
(3)
由 (1) 式和 (3) 式得
α + (−α) = 0
= k
1
ε
1
+ k
2
ε
2
+ ··· + k
n
ε
n
+ (−l
1
ε
1
− l
2
ε
2
− ··· − l
n
ε
n
)
= (k
1
− l
1
)ε
1
+ (k
2
− l
2
)ε
2
− ··· − (k
n
− l
n
)ε
n
(4)
因为 ε
1
, ε
2
, ··· , ε
n
线性无关,所以将 (4) 式的 n 项任意分为两部分,这两部分不可能互为逆元。
因此,(k
1
−l
1
)ε
1
, (k
2
−l
2
)ε
2
, ··· , (k
n
−l
n
)ε
n
这 n 项必须全为零向量,上述等式才能成立。又因
为 (k
1
−l
1
), ( k
2
−l
2
), ··· , (k
n
−l
n
) 不全为 0,设 (k
i
−l
i
) 不为 0,则 ε
i
必须为零向量,才使得
(k
i
−l
i
)ε
i
为零向量。因为任何包含零向量的向量组必然线性相关,所以 ε
1
, ε
2
, ··· , ε
n
线性相关。
这与
ε
1
,
ε
2
,
···
,
ε
n
是
V
的一组基产生矛盾,因此,
V
中不存在一个向量
α
,由
ε
1
,
ε
2
,
···
,
ε
n
线性表出时,表示法不是唯一的。
至此,证得命题 I。由命题 I 可知,V 的所有向量在法则 σ 下,在 P
n
中都有且只有一个像。因
此,法则 σ 是 V 到 P
n
的一个映射。
若 V 中有两个向量 α, β 由 ε
1
, ε
2
, ··· , ε
n
线性表出时,它们的表示法相同,则显然 α = β。因
此,V 中不同的向量在 P
n
中有不同的像,即 σ 是一个单射。
至此,第 1、2 个命题已经证得,现在来证第 3 个命题。要证 σ 是一个满射,即证明 P
n
中所有
元素在 V 中都有一个原像。
先来看 1 维线性空间的情形。因为 V 对数乘运算是封闭的,所以
kα ∈ V, ∀α ∈ V, ∀k ∈ P
此时,P 中所有元素在 V 中都有一个原像。对于 2 维线性空间的情形,因为 V 对向量加法和
数乘是封闭的,所以
k
1
α
1
+ k
2
α
2
∈ V, ∀α
i
∈ V, ∀k
i
∈ P, i = 1, 2
此时,P
2
中所有元素在 V 中都有一个原像。对于 3 维线性空间的情形,
(k
1
α
1
+ k
2
α
2
) + k
3
α
3
, ∀α
i
∈ V, ∀k
i
∈ P, i = 1, 2, 3
121

8.5 附录 V 补充证明
因为 (k
1
α
1
+ k
2
α
2
) ∈ V 且 k
3
α
3
∈ V ,所以
(k
1
α
1
+ k
2
α
2
) + k
3
α
3
∈ V, ∀α
i
∈ V, ∀k
i
∈ P, i = 1, 2, 3
此时,P
2
中所有元素在 V 中都有一个原像。对于 n 维线性空间的情形,可以依此类推。因此,
P
n
中所有元素在 V 中都有一个原像,即 σ 是一个满射。
至此,已证明第 1、2、3 个命题,原命题得证。
命题 8.3 V 是域 P 上的线性空间,W 是一个集合,若存在线性映射 A : V 7−→ W ,则
ran A ⊆ W ,ran A 也是域 P 上的线性空间。
证明. 已知线性映射 A 具有以下性质:
A (α + β) = A (α) + A (β)
A (kα) = kA (α)
(1)
要证明 W 是线性空间,即证明 W 可定义向量加法和数乘运算,它们符合线性空间的八个规则,
且 W 对这两者具有封闭性。由 (1) 式可知,W 显然可以定义向量加法和数乘。先来证向量加法
和数乘的封闭性。
∵ ∀α, β ∈ V, (α + β) ∈ V
∴ A (α), A (β) ∈ W, A (α + β) ∈ W
∵ ∀k ∈ P, ∀α ∈ V, kα ∈ V
∴ A (α) ∈ W, A (kα ) = kA ( α ) ∈ W
再来证明 W 也符合线性空间的八个规则。对于向量加法的结合律:
∵ (α + β) + γ = α + (β + γ)
∴ A [(α + β) + γ] = A [α + (β + γ)]
∴ A (α + β) + A (γ) = A (α) + A (β + γ)
∴ [A (α) + A (β)] + A ( γ) = A (α) + [ A (β) + A (γ)]
对于向量加法的交换律:
∵ α + β = β + α
∴
A
(
α
+
β
) =
A
(
β
+
α
)
∴ A (α) + A (β) = A (β) + A (α)
向量加法存在单位元:
∵ 0 + α = α, ∀α ∈ V
∴ A (0 + α) = A (0) + A (α) = A (α), ∀A (α ) ∈ W
注意,α 是 V 中的任意元素,因此 A ( α ) 也是 W 中的任意元素,所以 A (0) 就是 W 的向量
加法单位元。
W 中任意元素存在向量加法逆元:
∵ ∀α ∈ V, ∃β ∈ V, α + β = 0
∴ ∀A (α) ∈ W, ∃A (β) ∈ V, A (α + β) = A (α) + A (β) = A (0)
对于余下四条规则,也可以
122
